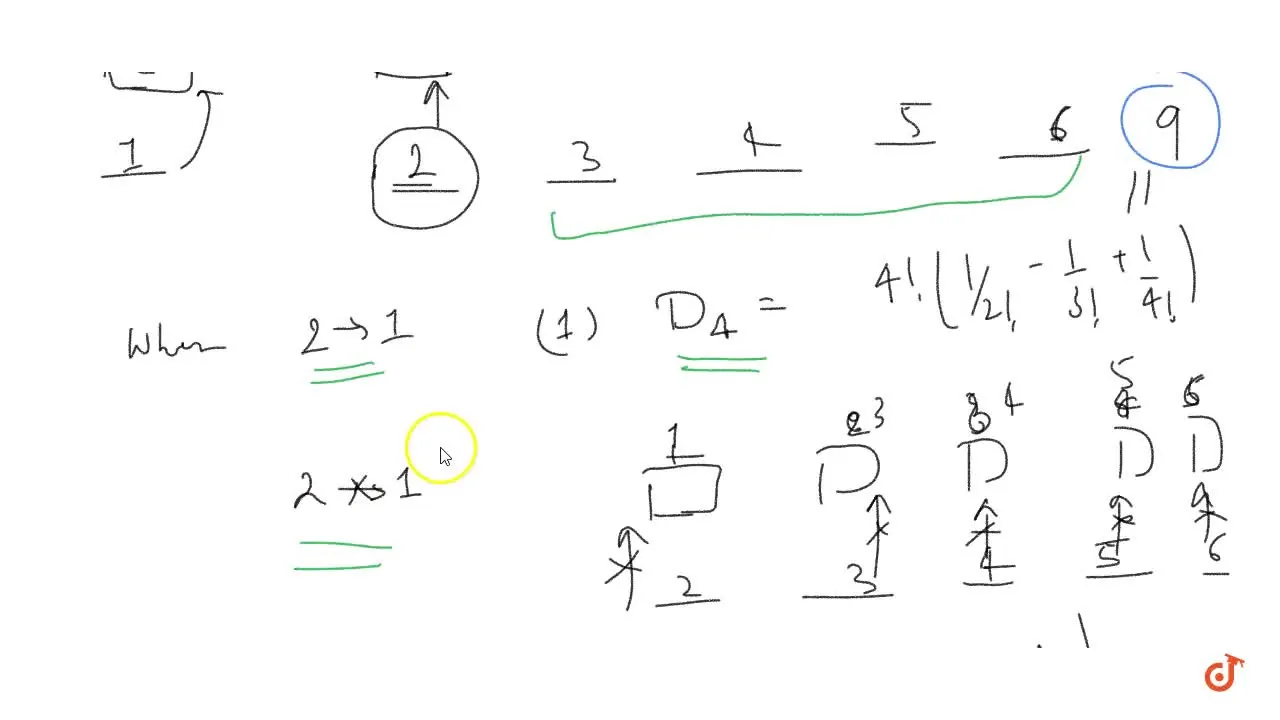
Six cards and six envelopes are numbered 1, 2, 3, 4, 5, 6 and cards are to be placed in envelopes so that each envelope contains exactly one card and no card is placed in the envelope bearing the same number and moreover cards numbered 1 is always placed in envelope numbered 2. Then the number of ways it can be done is
264
265
53
67
The correct Answer is:C
∵Card numbered 1 is always placed in envelope numbered 1, we can consider two cases.
Case I Card numbered 2 is placed I envelope numbered 1, then it is derangement of 4 objects, which can be done in
4!(1−11!+12!−13!+14!)=9 ways
Case II card numbered 2 is not placed in envelope numbered 1, then it is derangement of 5 objects, which can be done in
5!(1−11!+12!−13!+14!−15!)=44 ways
∴Total ways=9+44=53 ways.
Related Playlists
- BOOK - ARIHANT MATHSCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Subjective Type Questions)17videos
PERMUTATIONS AND COMBINATIONS
- BOOK - ARIHANT MATHSCHAPTER - PARABOLAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)36videos
PARABOLA
- BOOK - ARIHANT MATHSCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)55videos
PROBABILITY
Similar Questions
There are n letters and n corresponding envelopes. In how many ways the letters can be placed in the enveloped (one letters in each envelope) so that no letter is put in the right envelop.
View SolutionThe number of ways in which 5 letters can be placed in 5 marked envelopes, so that no letter is in the right encelope, is
View SolutionThere are 4 envelops and 4 letters are to be put in these envelopes randomly, then number of ways such that at least 2 letters are placed in wrong envelope.
View SolutionThere are 3 letters and 3 envelopes. Find the number of ways in which all letters are put in the wrong envelopes
View SolutionThere are 3 letters and 3 directed envelopes. Write the number of ways in which no letter is put in the correct envelope.
View SolutionThere sre three letters asnd three envelopes. Find the total number of wys in which letters can be put into the envelopes so that each envelope has only one letter.
View Solution52 cards are to be distributed among 4 players such that 2 players get 12 cards each and other 2 players get 14 cards each, then the number of ways in which this can be done is
View SolutionThere are 5 letters and 5 directed envelopes. The number of ways in which all the letters can be put in wrong envelope is
View SolutionRead the following information carefully and answer the questions given below:
(i) There are five types of cards viz. A,B,C,D and E. There are three cards of each type. These are to be inserted in envelopes of three colours -Red, Yellow and Brown. There are five envelopes of each colour.
(ii) B, D and E type cards are inserted in red envelopes A, B and C type cards are to be inserted in yellow envelopes and C, D and E type cards are to be inserted in brown envelopes.
(iii) Two cards each of B and D type are inserted in red envelopes.
Which of the following combinations of types of cards and the number of cards and colour of envelope is definitely correct?View SolutionRead the following information carefully and answer the questions given below:
(i) There are five types of cards viz. A,B,C,D and E. There are three cards of each type. These are to be inserted in envelopes of three colours -Red, Yellow and Brown. There are five envelopes of each colour.
(ii) B, D and E type cards are inserted in red envelopes A, B and C type cards are to be inserted in yellow envelopes and C, D and E type cards are to be inserted in brown envelopes.
(iii) Two cards each of B and D type are inserted in red envelopes.
Which of the following combinations of colour of the envelope and the number of cards is definitely correct in respect of E-type cards?View Solution