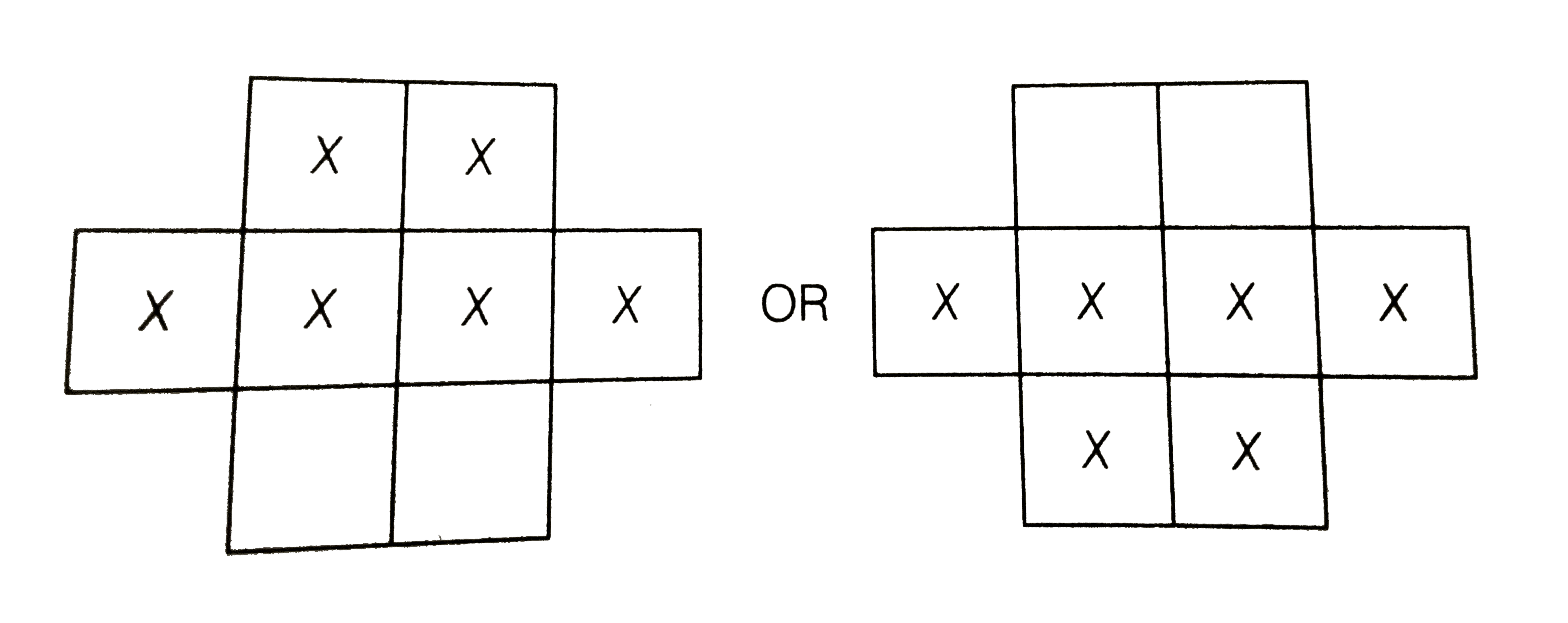
Six X 's have to be placed in the squares of the figure below, such that each row contains atleast one X. in how many different ways can this be done?

In the given figure there are 8 squares and we have to place 6X's this can be donne in
.8C6=.8C2=8⋅71⋅2=28 ways
But these include the possibility that either headed row or lowest row may not have any X. these two possibilities are to be excluded.
∴ Required number of ways=28-2=26
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHSCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - JEE Type Solved Examples: Single Matching Type Questions
1 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHSCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise For Session 1
11 Videos
- PARABOLABOOK - ARIHANT MATHSCHAPTER - PARABOLAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
36 Videos
- PROBABILITYBOOK - ARIHANT MATHSCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
55 Videos
Similar Questions
Six X ' s have to be placed in thesquares of the figure below, such that each rowcontains atleast one X. In how many different wayscan this be done?
View SolutionSix Ps have to be placed in the squares of the diagram given below such that each column contains at least one P. In how many ways this can be done?

View Solution
Knowledge Check
Six X ' s have to be placed in thesquares of the figure below, such that each rowcontains atleast one X. In how many different wayscan this be done?
A27B28C26D35
Six X's are to be placed in boxes of the figure such that each row contains at least one X, In how many different ways can this be done?A28B27C26D29Six X have to be placed in the squares of Fig. 6.6 such that each row contain at least one X. The number of ways in which this can be done is
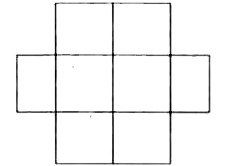 A25B26C27D30
A25B26C27D30
Six X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:
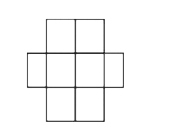
View SolutionSix X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:

View SolutionIn how many different ways 5 girls can be seated in a row?
View SolutionThe number of ways in which 5 X's can be placed in the squares of the figure so that no row remains empty is:
View Solution4 boys and three girls are to be seated in a row in such way that no two boys sit adjacent to each other in how many different ways can it be done?
View Solution
