सिद्ध कीजिए कि (i) 1−sinθ1+sinθ=(secθ−tanθ)2(ii)1−cosθ1+cosθ=(cosecθ−cotθ)2
L.H.S. =1−sinθ1+sinθ=1−sinθ1+sinθ×1−sinθ1−sinθ=(1−sinθ)21−sin∘θ=(1−sinθ)21−sin2θ=(1−sinθ)2cos2θ
=(1−sinθcosθ)2=(1cosθ−sinθcosθ)2=(secθ−tanθ)2
R.H.S. से आरम्भ कर भी हम आसानी से L.H.S. प्राप्त कर सकते है ।
(ii) L.H.S. =1−cosθ1+cosθ=1−cosθ1+cosθ×1−cosθ1−cosθ
=(1−cosθ)21−cos2θ=(1−cosθ)2sin2θ
=(1−cosθsinθ)2=(1sinθ−cosθsinθ)2
=(cosecθ−cosθ)2=R.H.S.
Topper's Solved these Questions
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ Book:KC SINHAChapter:त्रिकोणमितीय अनुपात और सर्वसमिकाएँ Exercise:EXERCISE 8.1
Explore 65 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ Book:KC SINHAChapter:त्रिकोणमितीय अनुपात और सर्वसमिकाएँ Exercise:लघु उत्तरीय प्रश्न
Explore 87 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग Book:KC SINHAChapter:त्रिकोणमिति के कुछ अनुप्रयोग Exercise:वस्तुनिष्ठ प्रश्न
Explore 14 Videos
- त्रिभुज Book:KC SINHAChapter:त्रिभुज Exercise:वस्तुनिष्ठ प्रश्न
Explore 28 Videos
Similar Questions
दिए गये चित्र से निम्नलिखित के मान ज्ञात कीजिए :
(i) sinC (ii)sinA
(iii) cosC (iv)cosA
(v) tanC (vi)tanA
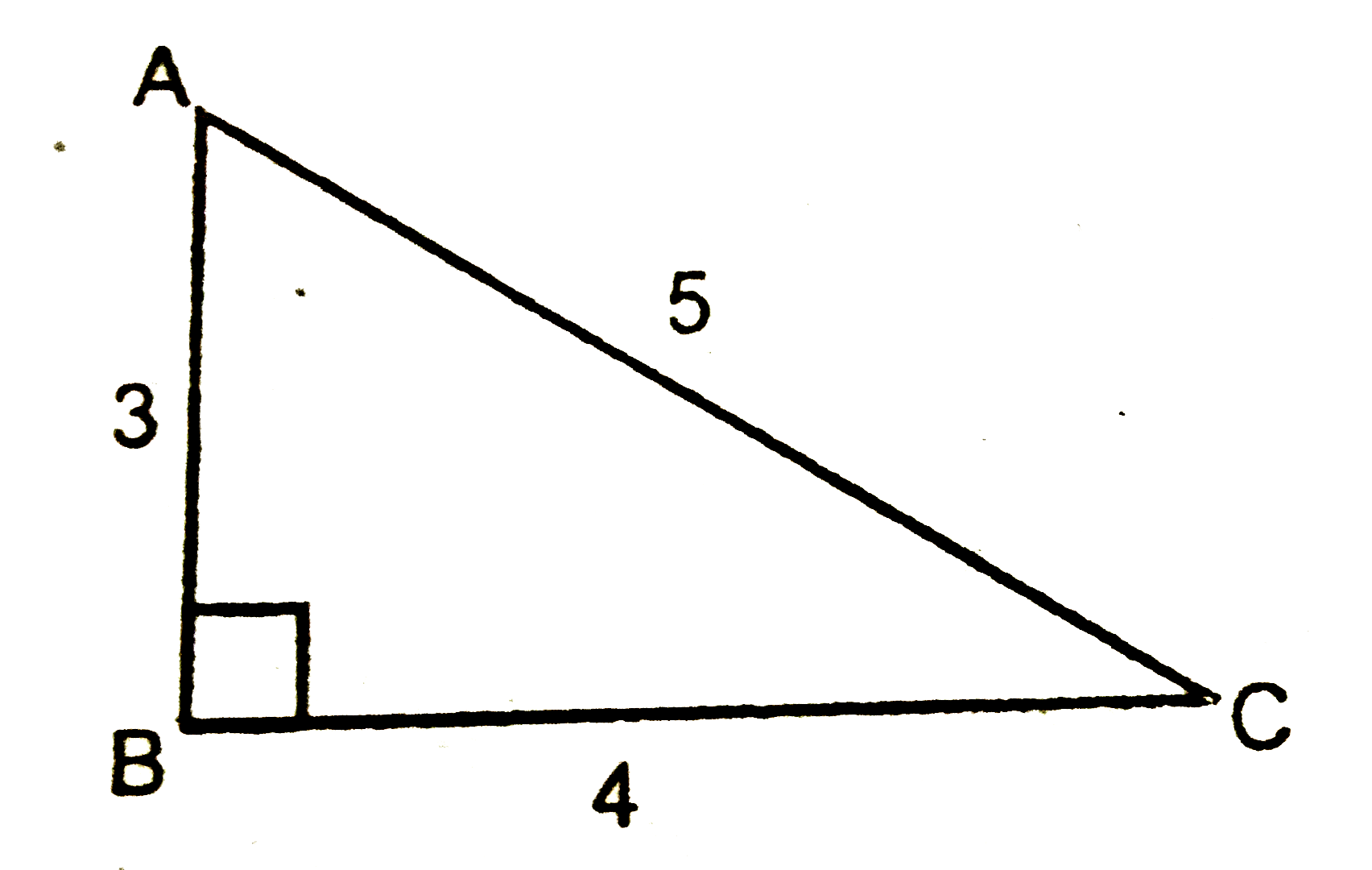
View Solutionयदि tanA=ba,जहाँ a और b वास्तविक संख्याएँ है , तो sin2A का मान ज्ञात करें ।
View Solutionयदि एक मीनार के पाद से 100 m दूर स्थित बिंदु पर मीनार का उन्नयन कोण60∘ है , तो मीनार कि ऊँचाई है :
View SolutionΔABC में DE∣∣BC और ADDB=53 तब AEAC=
View SolutionProve that (sin theta)/(sec theta+tan theta-1)+cos theta/(cosec theta+cot theta-1)=1
View SolutionProve that: ((1)/(cos theta)-(1)/(sin theta))(1+(sin theta)/(cos theta)+(cos theta)/(sin theta))=sec theta tan theta-cosec theta cot theta
View SolutionProve that
(sinθ−cosecθ)(cosθ−secθ)=1tanθ+cotθ.
View SolutionProve that
(i)1−sinθ1+sinθ=(secθ−tanθ)2
(ii)(1+cosθ)(1−cosθ)=(cosecθ+cotθ)2
View Solutionसर्वसमिकाओ को सिद्ध करो :
sinθ1−cosθ+tanθ1+cosθ=secθcosecθ+cotθ
View Solutionसिद्ध कीजिए कि sinθ(1+tanθ)+cosθ(1+cotθ)=secθ+cosecθ
View Solutionसिद्ध कीजिए : sinθsecθ+tanθ−1+cosθ cosec θ+cotθ−1=1
View SolutionProve that tanθ+sinθtanθ−sinθ=secθ+1secθ−1
OR
Prove that (cosecθ−cotθ)2=1−cosθ1+cosθ
View Solutiontan2θtan2θ−1+cos2θsin2θ−cos2θ=1sin2θ−cos2θ=tan2θtam2θ−1+cosec2θsec2θ−cosec2θ
View SolutionProve that
(1+cotθ+tanθ)(sinθ−cosθ)=secθcosec2θ−cosecθsec2θ.
View SolutionProve that: sinθ(1+tanθ)+cosθ(1+cotθ)=secθ+cosecθ.
View Solution

