समबाहु ΔABC में, D बिन्दु, भुजा BC पर इस प्रकार है कि BD=13BC सिद्ध करें कि 9AD2
एक त्रिभुज ABC है जिसमे AB=BC=CA और D एक बिन्दु BC पर इस प्रकार है कि BD=13BC
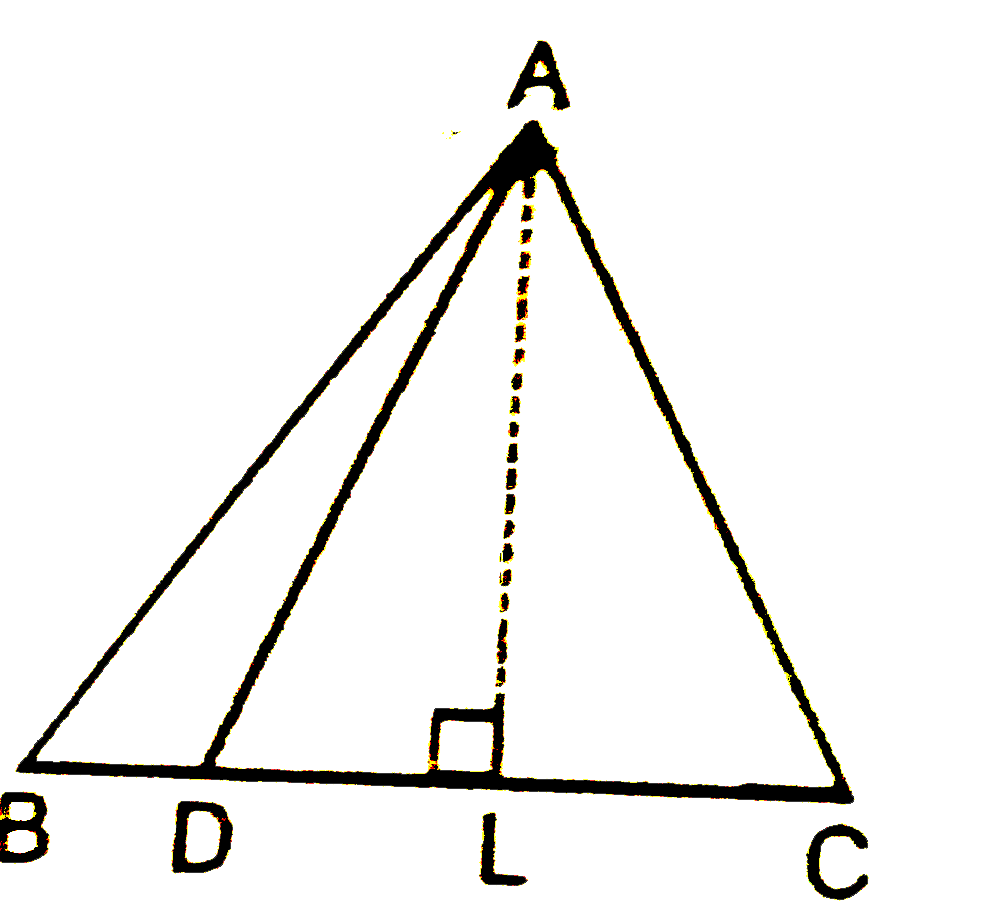
सिद्ध करना है : 9AD2=7AB2
रचना :AL⊥BC खींचा ।
उपपत्ति : समकोण त्रिभुजों ALB और ALC में, AB=AC (दिया है)
और AL=AL ( उभयनिष्ट)
∴ΔALB=ΔALC(RHS अभिगृहित से)
अतः BL=CL
इस प्रकार BD=13BC और BL=12BC अब ΔALB में, ∠ALB=90∘
∴AB2=AL2+BL2 (पाइथागोरस प्रमेय से) ....(i)
पुनः ΔALD में , ∠ALD=90∘
∴AD2=AL+DL2 (पाइथागोरस प्रमेय से)
=AL2+(BL−BD)2=AL2+(BL2+BD2−2BL.BD)
=AL2+BL2)+BD2−2BL.BD
=AB2+BD2−BL.BD [(i) से]
=BC2+(13BC)2−2(12BC).13BC[∵AB=BC,BD=13BCऔरBL=12BC]
Topper's Solved these Questions
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.1
22 Videos
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )
8 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.4
85 Videos
- दो चर वाले रैखिक समीकरण युग्मBOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न
44 Videos
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)
View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
View SolutionIn an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionΔABC is an equilateral triangle . D is a point on the side BC such that BD=13BC. Prove that 7AB2=9AD2
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
View Solutionकिसी ΔOAB में ∠AOB=90∘ तथा बिन्दु P, Q भुजा AB को समत्रिभाजित करते हैं | सिद्ध कीजिए कि, OP2+OQ2=59AB2.
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View SolutionBD = 1/3 BC ಆಗುವಂತೆ ಸಮಬಾಹು ತ್ರಿಭುಜ ABC ಯಲ್ಲಿ D ಯು BCಯ ಮೇಲಿನ ಒಂದು ಬಿಂದುವಾಗಿದೆ. 9AD2=7AB2ಎಂದು ಸಾಧಿಸಿ.
View SolutionIn an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionIn equilateral DeltaABC, D is a point on BC such that BD=13BC. Prove that 9AD2=7AB2.
View Solutionਕਿਸੇ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ BC 'ਤੇ ਇਕ ਬਿੰਦੂ D ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ BD=1/3 BC ਹੈ,ਸਿੱਧ ਕਰੋ ਕਿ 9AD2=7AB2 ਹੈ।
View SolutionIn an equilateral triangle ABC. D is a point on side BC such that BD=1/3 BC. Prove that 9AD2=7AB2.
View Solution
