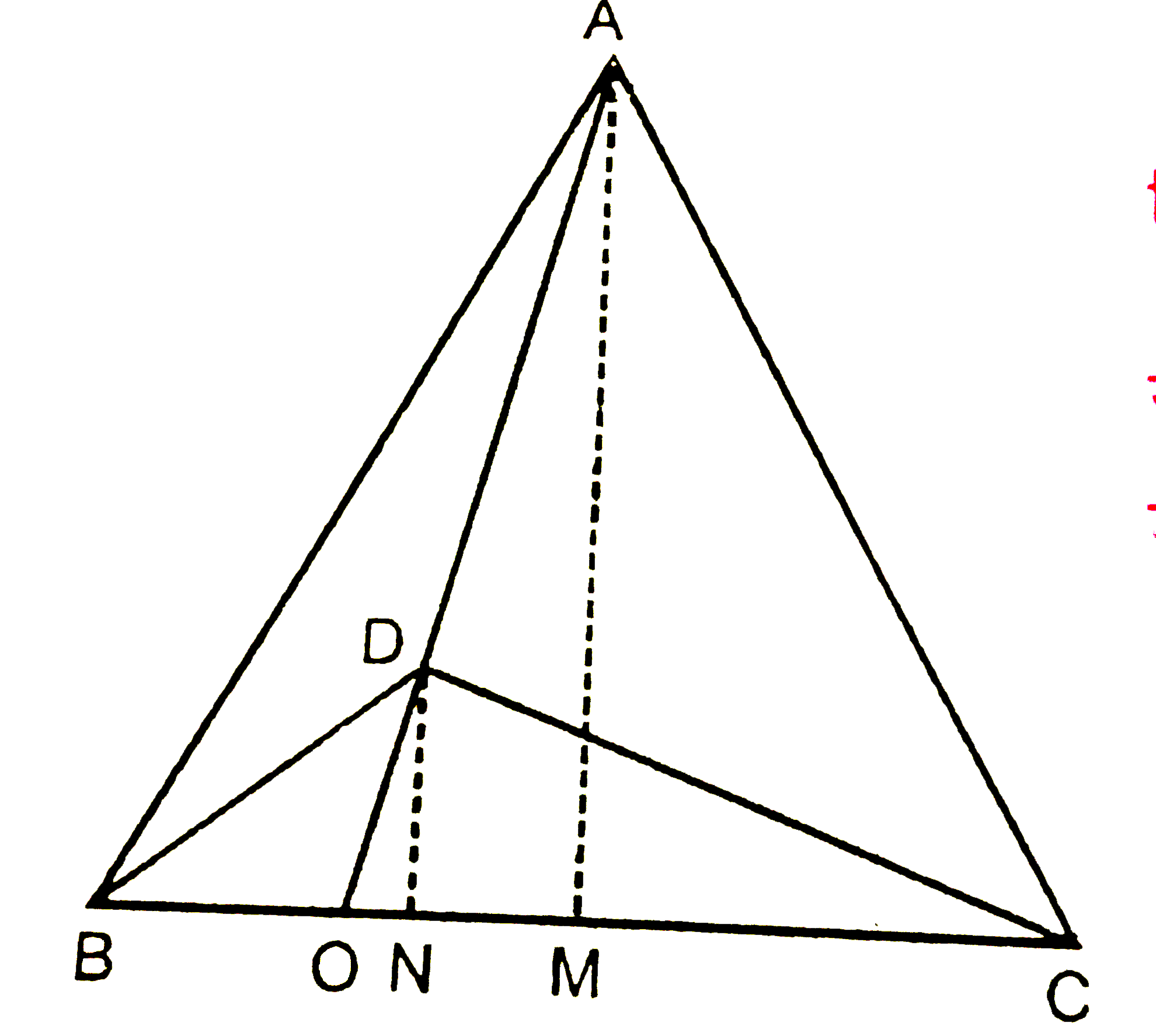
दिए गए चित्र में ABC और DBC दो त्रिभुज एक ही आधार BC पर स्थित है । यदि AD,BC को O पर प्रतिच्छेद करती है , तो दिखाएँ कि ar(ΔABC)ar(ΔBCD)=AODO
ΔABC और ΔBCD एक ही आधार BC पर स्थित है और AD,BC को O पर प्रतिच्छेद हारती है ।
सिद्ध करना है कि क्षे०(ΔABC)क्षे०(ΔBCD)=AODO
रचना AM⊥BC और DN⊥BC खींचा ।
उपपत्ति : ΔAMOऔर ΔDNO में
∠M=∠N(प्रत्येक=90∘)
anag≤AOM=∠DON (उभयनिष्ट कोण)
∴ΔAMO~ΔDNO (A Aउप -प्रयेय से)
∴AODO=AMDN
=12×BC×AM12×BC×DN
क्षे०(ΔABC)क्षे०(ΔBCD) (प्रमाणित)
Topper's Solved these Questions
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.1
22 Videos
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )
8 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.4
85 Videos
- दो चर वाले रैखिक समीकरण युग्मBOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न
44 Videos
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)
View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
View SolutionIn Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that (ar (ABC))/( ar (DBC))= (AO )/( DO )
View SolutionIn the same figure, ΔABCandΔDBC are on the same base BC . If AD is intersects BC at O, prove that
ar(ΔABC)ar(ΔDBC)=AODO
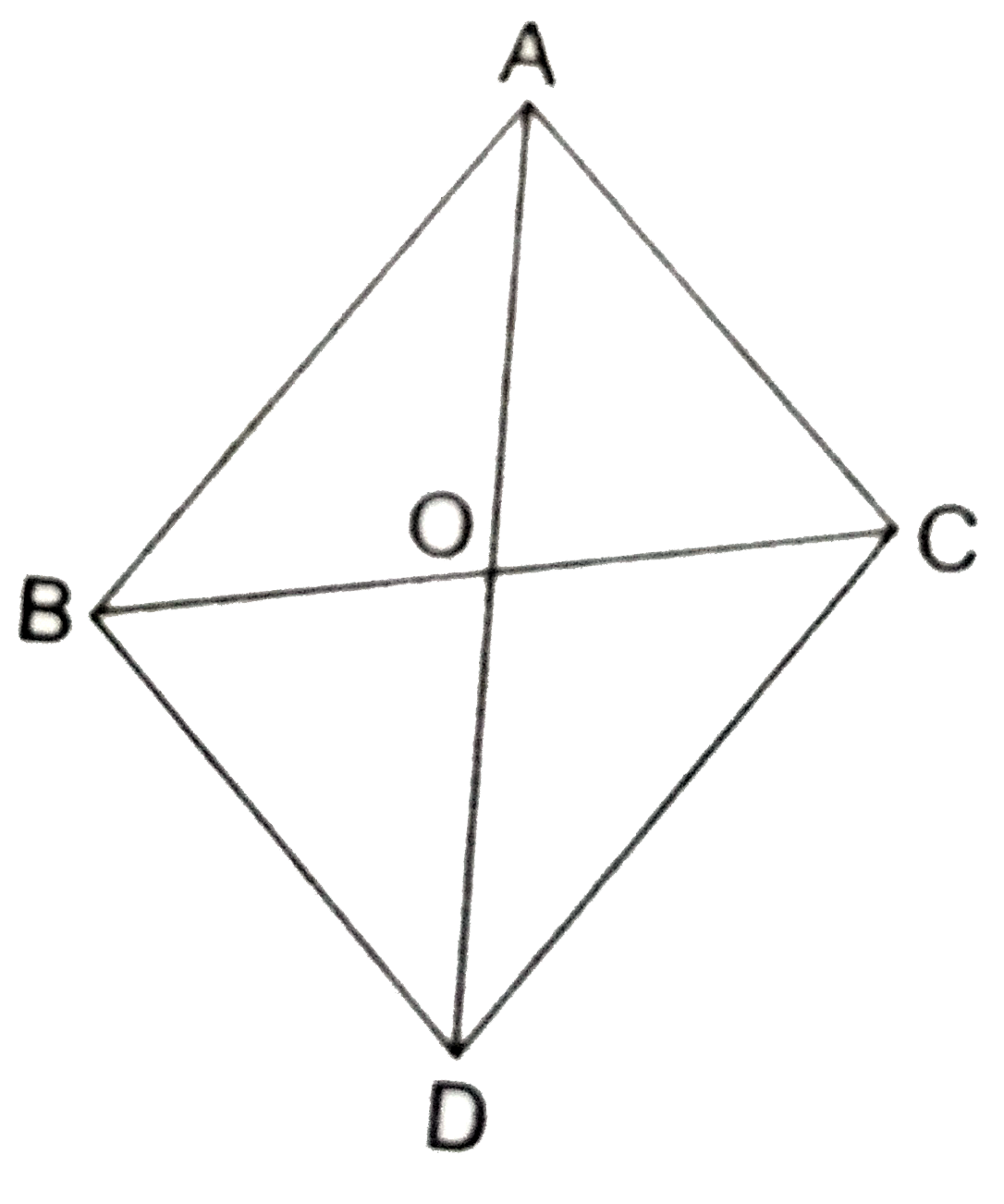
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
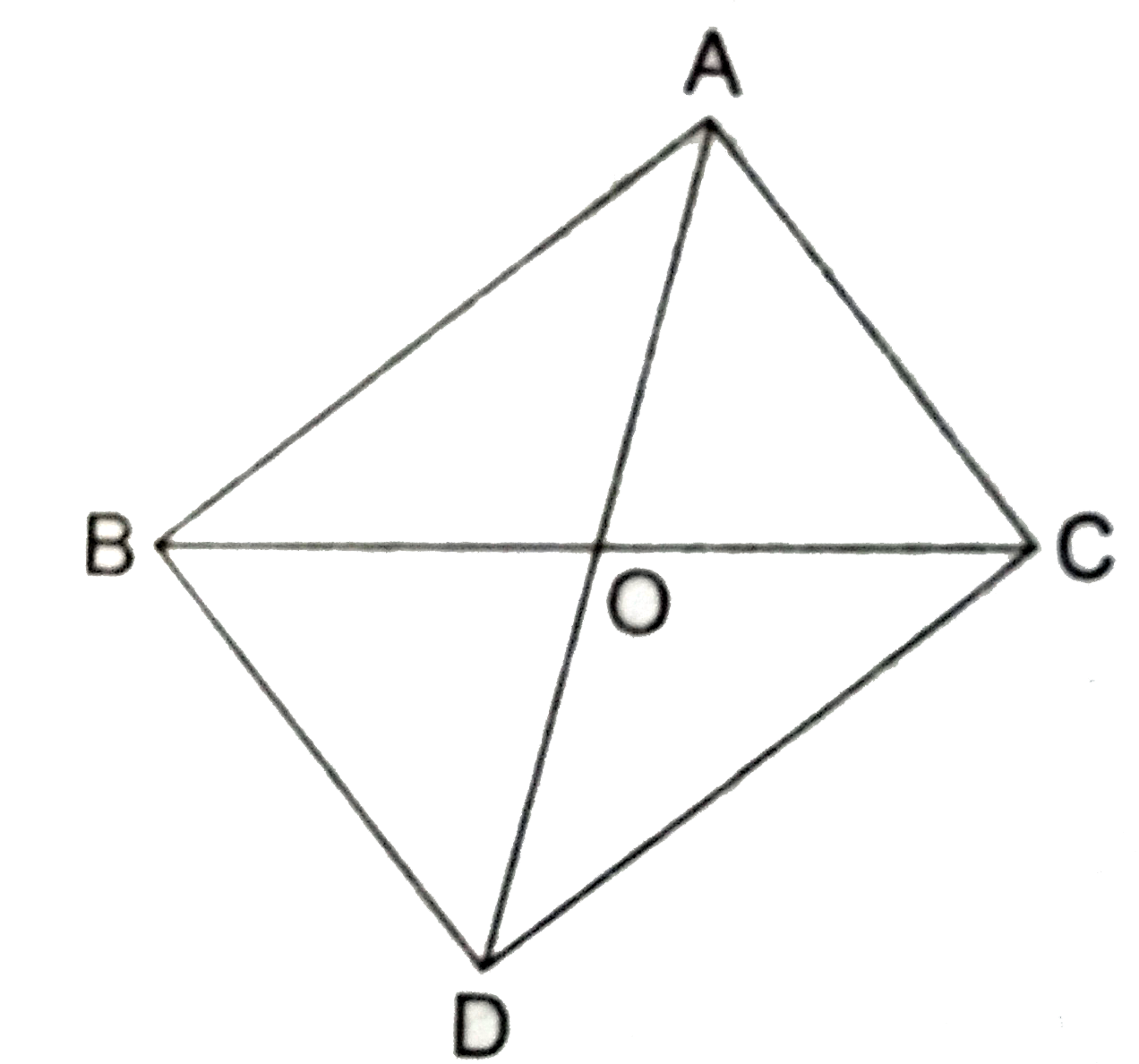
View Solutionआकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए है। यदि AD,BD को O पर प्रतिच्छेद पर तो दर्शाइए कि ar(ΔABC)ar(ΔDBC)=AODO है।
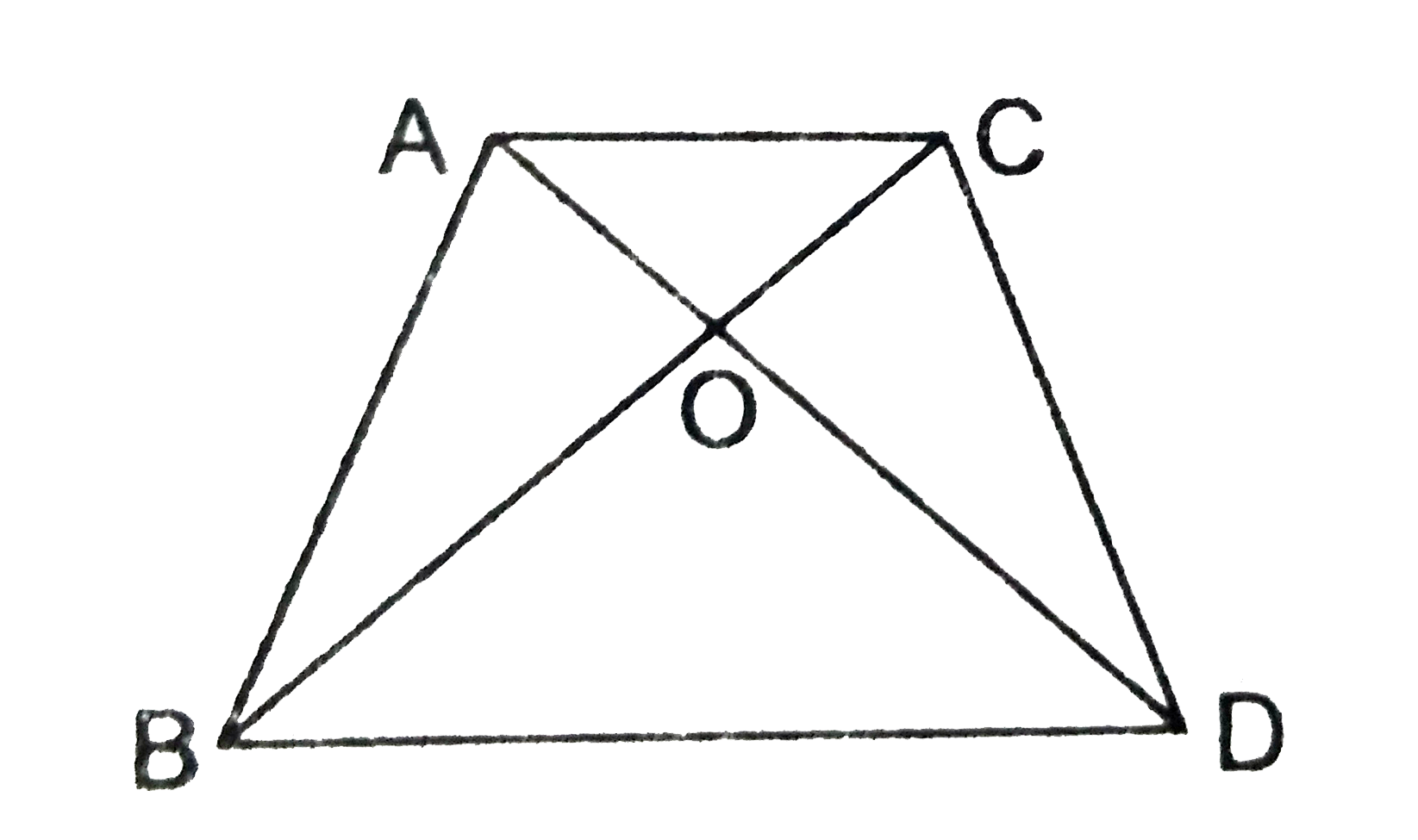
View SolutionIn Fig , ABC and DBC are two triangles on the same base BC. If AD intersects BC,at O , show that ar(ABC)ar(DBC)=AODO
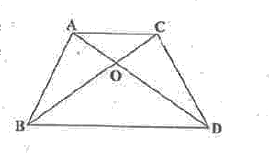
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View SolutionIn the figure given below, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ΔABC)ar(ΔDBC)=AODO.
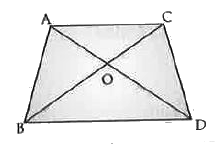
View SolutionIn the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.
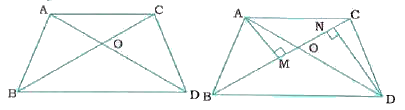
View SolutionIn the given figure, ABC and DBC are two triangles on the same base BC. Prove that ar(ABC)ar(DBC)=AODO.
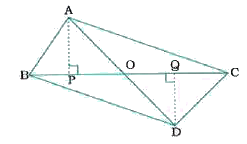
View Solutionਚਿੱਤਰ 6.44 ਵਿੱਚ ਇਕੋ ਆਧਾਰ BC ਉੱਤੇ ਦੋ ਤ੍ਰਿਭੁਜ ABC ਅਤੇ DBC ਬਣੇ ਹੋਏ ਹਨ। ਜੇਕਰ AD,BC ਨੂੰ O 'ਤੇ ਕੱਟੇ ਤਾਂ ਦਰਸਾਉ ਕਿ ar(ABC)ar(DBC)=AODO ਹੈ।
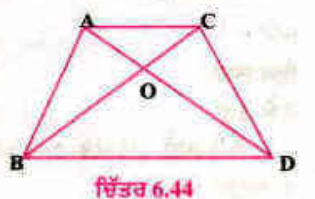
View SolutionIn Fig, ABCand DBC are lwo triangles on the same base BC. If AD intersects BC at O,show that ar(ABC)ar(DBC)=AODO.
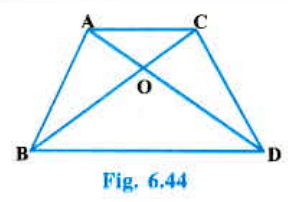
View SolutionIn triangle ABC , F and E are the points on sides AB and AC respectively, such that FE || BC and FE divides the triangle in two parts of equal area. If AD bot BC and AD intersect FE at G, then GD: AG = ? triangle ABC में F और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि FE || BC है तथा FE त्रिभुज को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है | यदि AD bot BC है और AD, FE को G पर काटती है, तो GD: AG = ?
View Solution
