Question

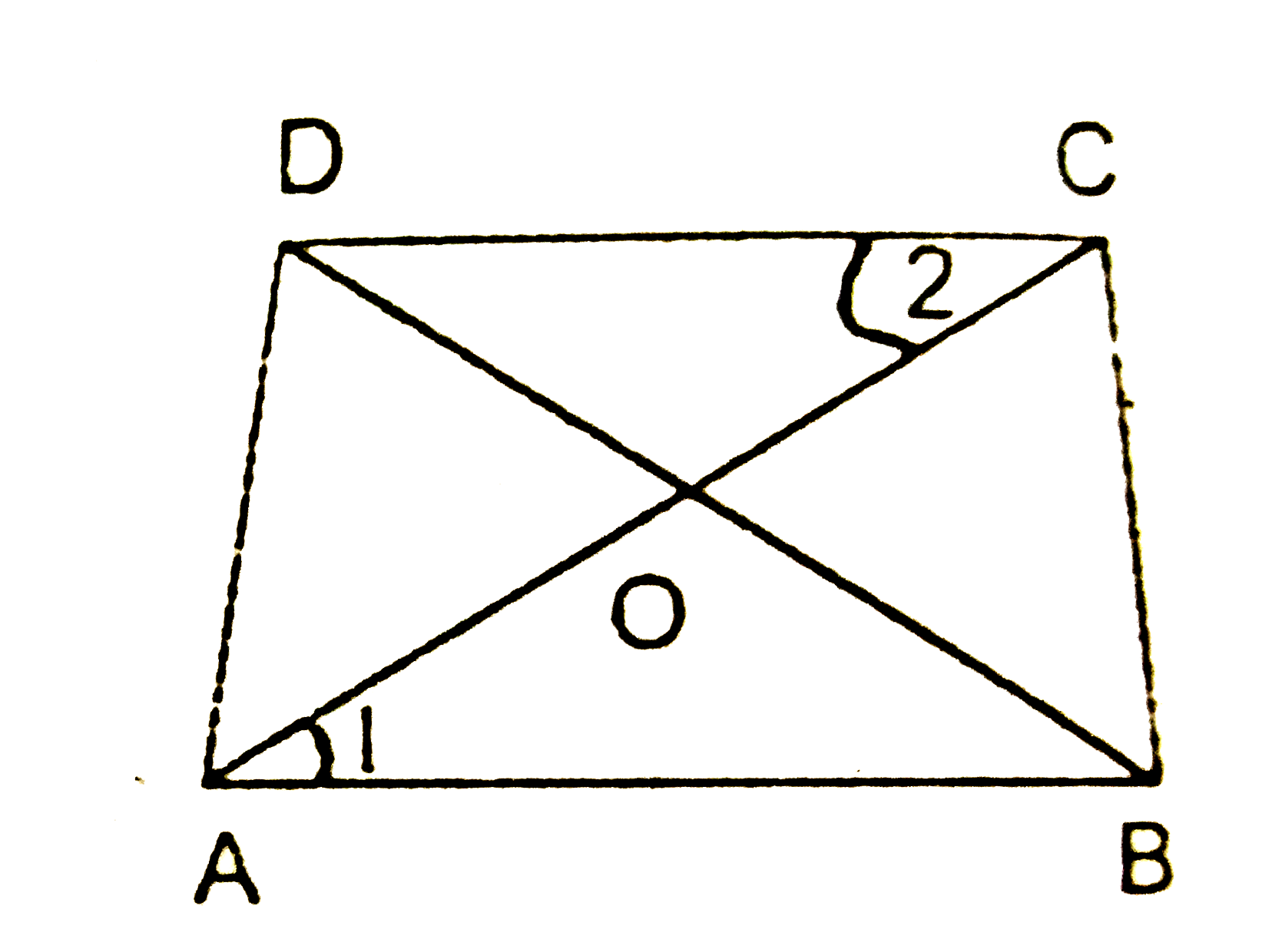
यदि किसी चतुर्भुज के विकर्ण एक -दूसरे को समानुपाती खण्डों में प्रतिच्छेद करते है , तो सिद्ध करें कि वह चतुर्भुज एक समलम्ब चतुर्भुज है ।

Explanation

ABCD एक समलम्ब चतुर्भुज है। जिसके विकर्ण एक -दूसरे को O पर इस प्रकार प्रतिच्छेद करते है कि `(AO)/(OC)=(BO)/(OD)`
सिद्ध करना है : ABCD एक समलम्ब चतुर्भुज है ।
उपपत्ति `(AO)/(OC)=(BO)/(OD)` ( दिया हुआ है)
`therefore (AO)/(OB)=(OC)/(OD)`
अब `Delta AOB` और `DeltaCOD` में ,
`angle AOB=angleCOD` (शीर्षभिमुख कोण से)
और `(AO)/(OB)=(OC)/(OD)`
`therefore DeltaAOB~DeltaCOD` [SAS समरूपता से]
`therefore angle2=angle1`
किन्तु यह एकान्तर अतः कोणों का एक युग्म है ।
`therefore AB||DC`
अतः ABCD एक समलम्ब चतुर्भुज है ।