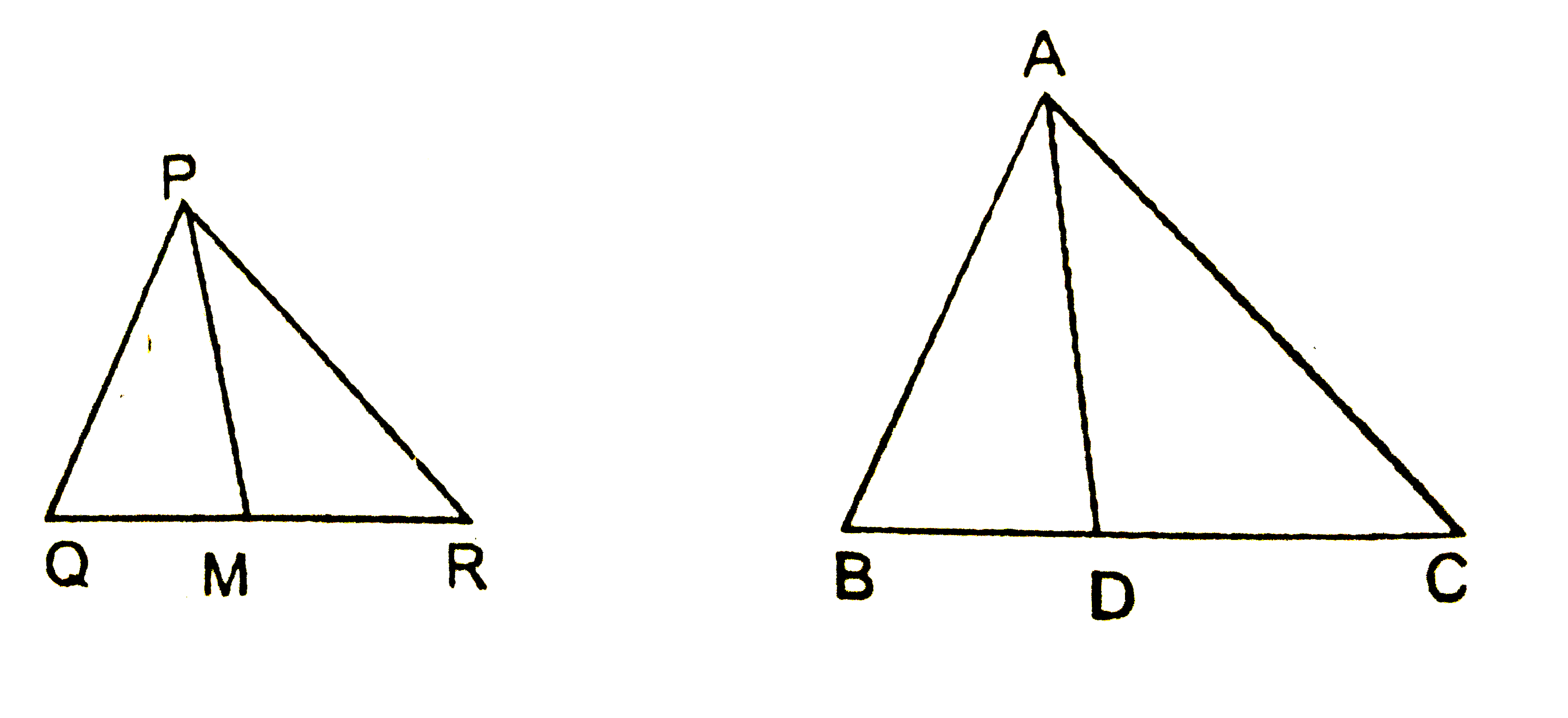
यदि AD और PM की क्रमशः मध्यिकाएँ है , और जहाँ सिद्ध करें कि
(i)
(ii)
दिया है : और इस प्रकार है कि उनकी मध्यिकाएँ AD,PM है और
सिद्ध करना है : (i)
(ii)
उपपत्ति :
और
किन्तु
(i) अब और में ,
और
(SAS समरूपता से)
अतः
(ii)
(प्रमाणित)
Topper's Solved these Questions
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.1
22 Videos
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )
8 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.4
85 Videos
- दो चर वाले रैखिक समीकरण युग्मBOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न
44 Videos
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)
View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
View SolutionAD और PM त्रिभुजों ABC और PQR कि क्रमशः मध्यिकाएँ है जबकि ΔABC~ΔPQR है सिद्ध कीजिए कि ABPQ=ADPM है
View Solutionएक त्रिभुज ABC की भुजाएं AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती है। दर्शाइए कि ΔABC~ΔPQR है।
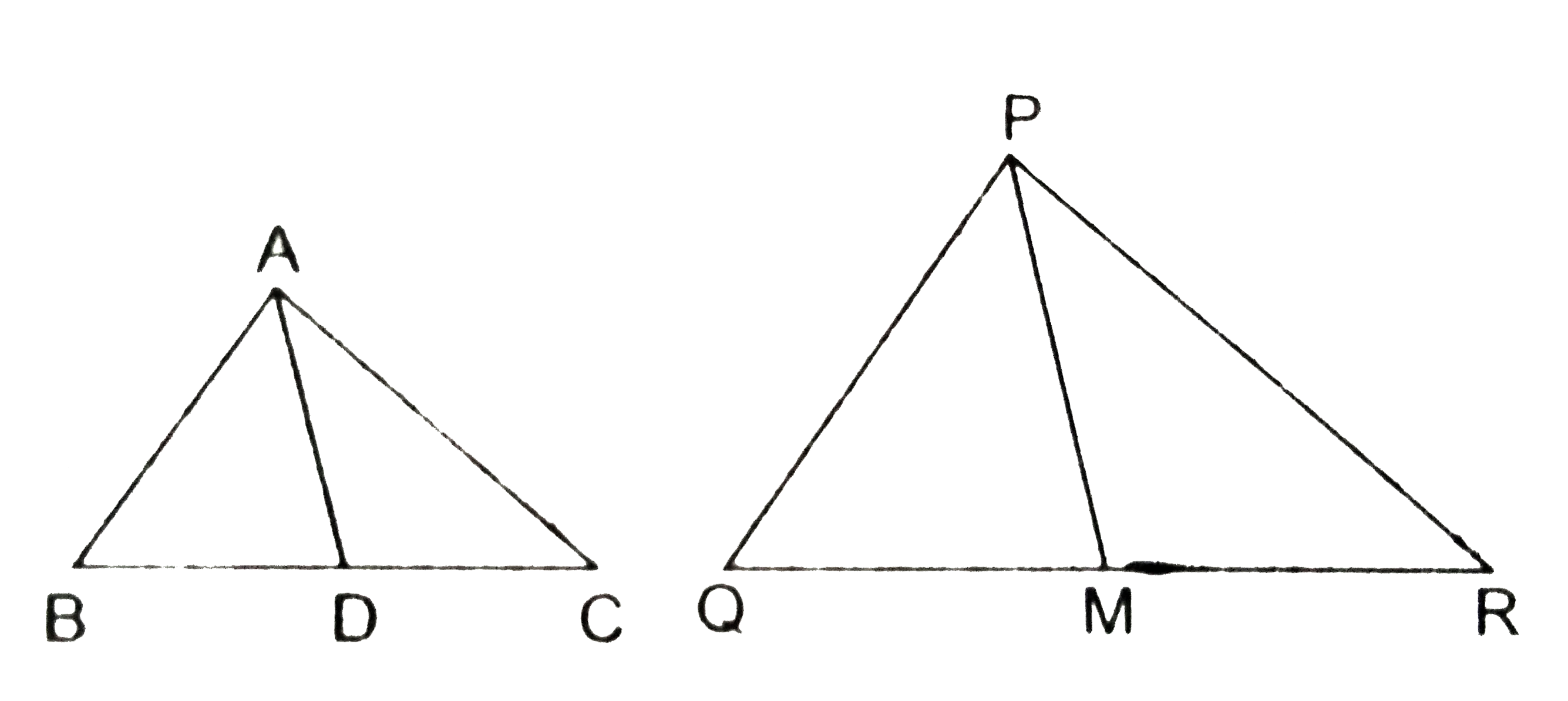
View SolutionAD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं , जबकि ΔABC~ΔPQR है । सिद्ध कीजिए कि ABPQ=ADPM है ।
View SolutionAD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं , जबकि ΔABC~ΔPQR है । सिद्ध कीजिए कि ABPQ=ADPM है ।
View Solutionयदि AD तथा PM क्रमशः △ABC तथा △PQR के समद्विभाजक है जहाँ △ABC~△PQR है तो सिद्ध कीजिए कि :
(i) ABPQ=ADPM
(ii) ∠ADC=∠PMR
View SolutionIf AD and PM be two medians of ΔABC and ΔPQR respectively, where ΔABC~ΔPQR, then prove that ABPQ=ADPM.
View SolutionΔABC की भुजाएँ AB और BC और माध्यिका AD क्रमशः ΔPQR की भुजाओं PQ और QR माध्यिका PM के बराबर है। सिद्ध कीजिए कि त्रिभुज ABC और PQR सर्वांगसम है।
View SolutionIf Adand PM are medians of triangles ABC and PQR, respectively where ΔABC~ΔPQR , prove that ABPQ=ADPM
View SolutionIf AD and PM are median of triangles ABC and PQR respectively where ΔABC−ΔPQR, prove that ABPQ=ADPM.
View SolutionIf AD and PM are medians of triangles ABC and PQR respectively , where ΔABC~ΔPQR, prove that ABPQ=ADPM.
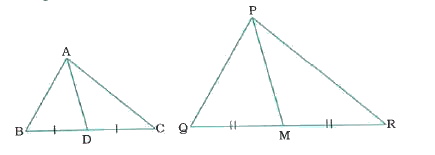
View SolutionIf AD and PM are medians of triangles ABC and PQR, respectively where △ABC~△PQR , Prove that ABPQ=ADPM .
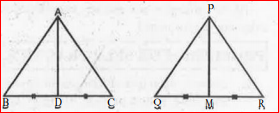 .
.
View Solution
