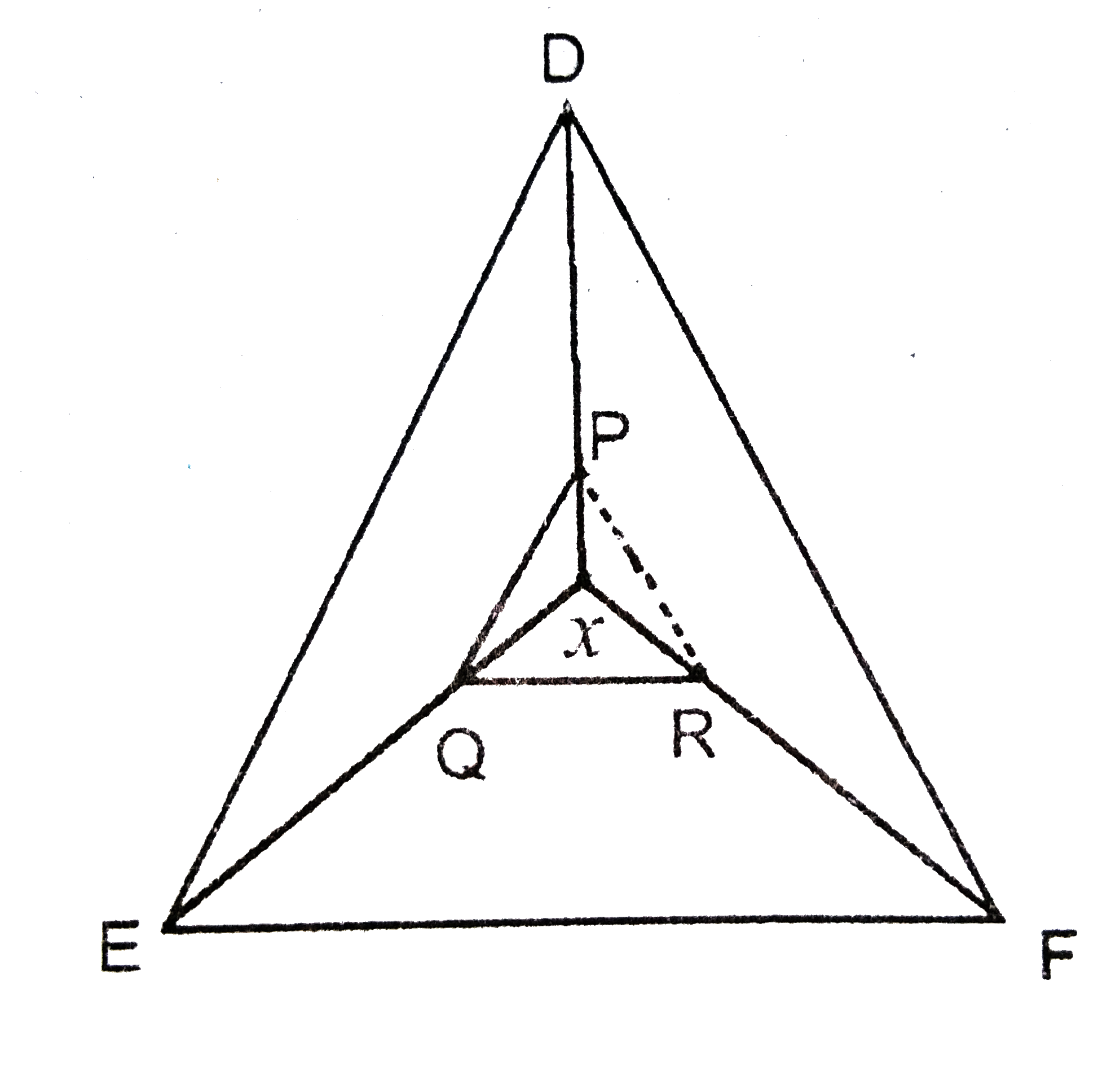
ΔDEF में कोई बिन्दु X है जिसे शीर्ष D,E तथा F से मिलाया गया है । DX पर कोई बिन्दु P लेकर , PQ∣∣DE खींचा गया है , जो XE से Q पर मिलती है तथा Q से QR∣∣EF जो XF से R पर मिलती है । सिद्ध करें कि PR∣∣DF.
दिया है : कोई बिन्दु X,ΔDEF में स्थित है ।
DX पर कोई बिन्दु P है । PQ∣∣DE जो XE को Q पर करती है तथा QR∣∣EF, जो XF को R काटती है ।
सिद्ध करना है कि PR∣∣DF
रचना : PR को मिला दिया
उपपत्ति : ΔXED में , PQ∣∣DE
∴XPPD=XQQE थेल्स के प्रमेय से ) ....(i)
पुनः ΔXEF में RQ∣∣EF
∴XQPD=XRRF (थेल्स के प्रमेय से) ....(ii)
(i) और (ii) से हम पाते है , XPPD=XRRF
ΔXFD में , बिन्दु R और P भुजाएँ XF और XD को समान अनुपात में बाँटती है ।
अतः थेल्स के आधारभूत समानुपातकता प्रमेय के विलोम से PR∣∣DF
Topper's Solved these Questions
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.1
22 Videos
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )
8 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.4
85 Videos
- दो चर वाले रैखिक समीकरण युग्मBOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न
44 Videos
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)
View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
View Solutionबिन्दु (1,0,0) से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो XZ-समतल पर लम्ब है।
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है और y -अक्ष से ऐसा अन्तः खण्ड काटती है जो कि x -अक्ष पर काटे अन्तः खण्ड को दो गुना है।
View Solutionकोई फलन किसी बिन्दु x = a पर अवकलनीय कहलता है, जब -
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solutionएक काले तथा लाल पासे को कर्म में उछाला गया है। तब
पासो पर प्राप्त अंको का योग 9 से अधिक होने कि सप्रतिबन्ध प्रायिकता ज्ञात करो यदि ज्ञात है कि काले पासे पर अंक 5 प्रकट हुआ है।
View Solutionयदि वृत्त x2+y+6x+6y=2 के बिन्दु P पर खींची गई स्पर्शी सरल रेखा 5x−2y+6=0 से y-अक्ष के बिन्दु Q पर मिलती है, तो PQ की लम्बाई है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionवक्र y(x−2)(x−3)=x+6 के उस बिन्दु पर जहाँ वक्र Y -अक्ष को काटता है, खींचा गया अभिलम्ब निम्न में से किस बिन्दु से होकर जाता है?
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि बिन्दु (2,α,β) उस समतल पर स्थित है, जो बिन्दुओ (3,4,2) तथा (7,0,6) से होकर जाता है तथा समतल 2x−5y=15 के लंबवत है, तो 2α−3β बराबर है
View Solution
