ABCD एक समलम्ब चतुर्भुज है जिसमे AB∣∣DC. E और F क्रमशः असमान्तर भुजाओं AD और BC पर दो बिन्दु है । इस प्रकार EF∣∣AB. दिखाये AEED=BFFC.
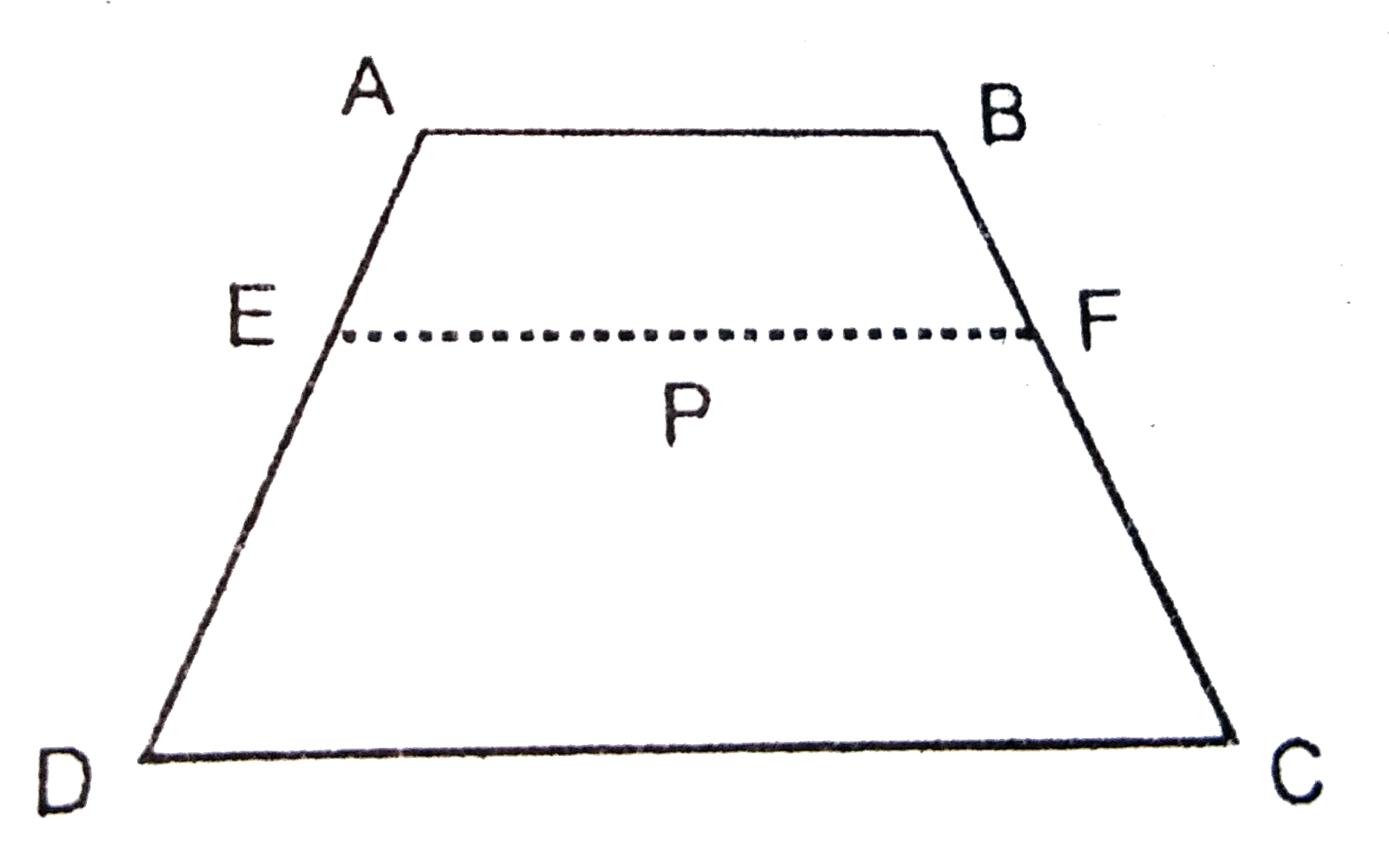
दिया है : ABCD एक समलम्ब चतुर्भुज है जिसमे AB∣∣DC तथा E और F क्रमशः भुजाएँ AD और BC पर दो बिन्दु इस प्रकार है कि EF∣∣AB
सिद्ध करना है कि : AEED=BFFC
रचना : AC को मिला दें जो EF को P पर प्रतिच्छेद करती है , अब (AB∣∣DC और (EF∣∣AB (दिया है )
∴EF∣∣DC [एक ही रेखा के समान्तर रेखाएँ आपस में समान्तर होती है।]
अब ΔADC में ,
EP∣∣DC
∴AEED=APPC (थेल्स के प्रमेय से)....(i)
इसी तरह ΔCAB से , CPAP=CFBF अर्थात, APPC=BFFC...(ii)
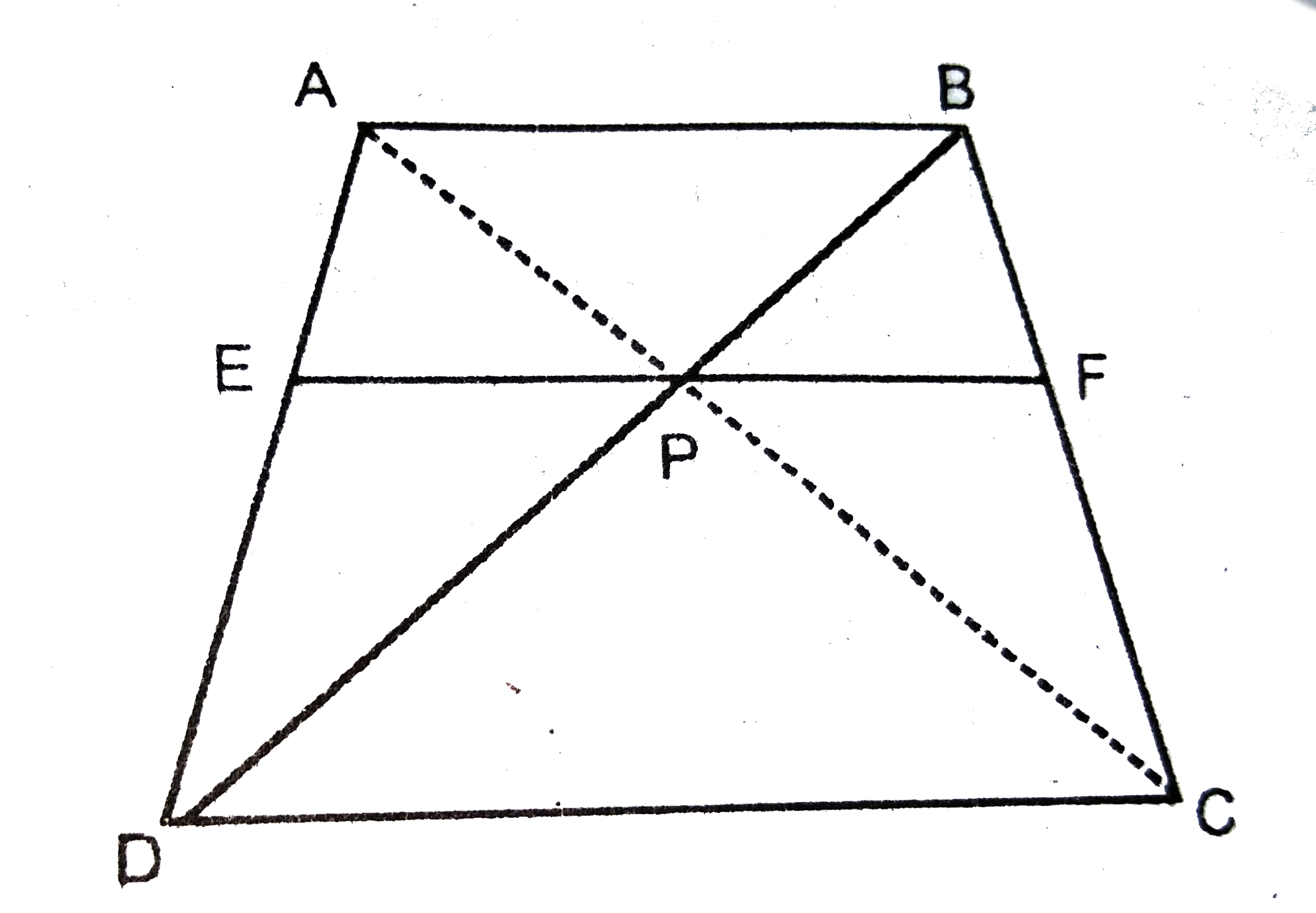
अतः (i) और (ii) से ,AEED=BFFC.
Topper's Solved these Questions
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.1
22 Videos
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )
8 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.4
85 Videos
- दो चर वाले रैखिक समीकरण युग्मBOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न
44 Videos
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)
View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
View SolutionABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
View SolutionABCD एक समलम्ब हैं जिसमे AB ||DC हैं । असमान्तर भुजाओं AD और BC पर क्रमशः बिन्दु E और F इस प्रकार स्थित हैं कि EF भुजा AB के समान्तर हैं दर्शाइए कि AEED=EFFC हैं ।
View SolutionABCD एक समलम्ब चतुर्भुज है । जहा AB।।DC बिन्दु E तथा F, क्रमशः असमान्तर भुजाओं AD तथा BC पर है तथा EF, AB के समान्तर है । तो सिद्ध कीजिए कि
AEED=BFFC
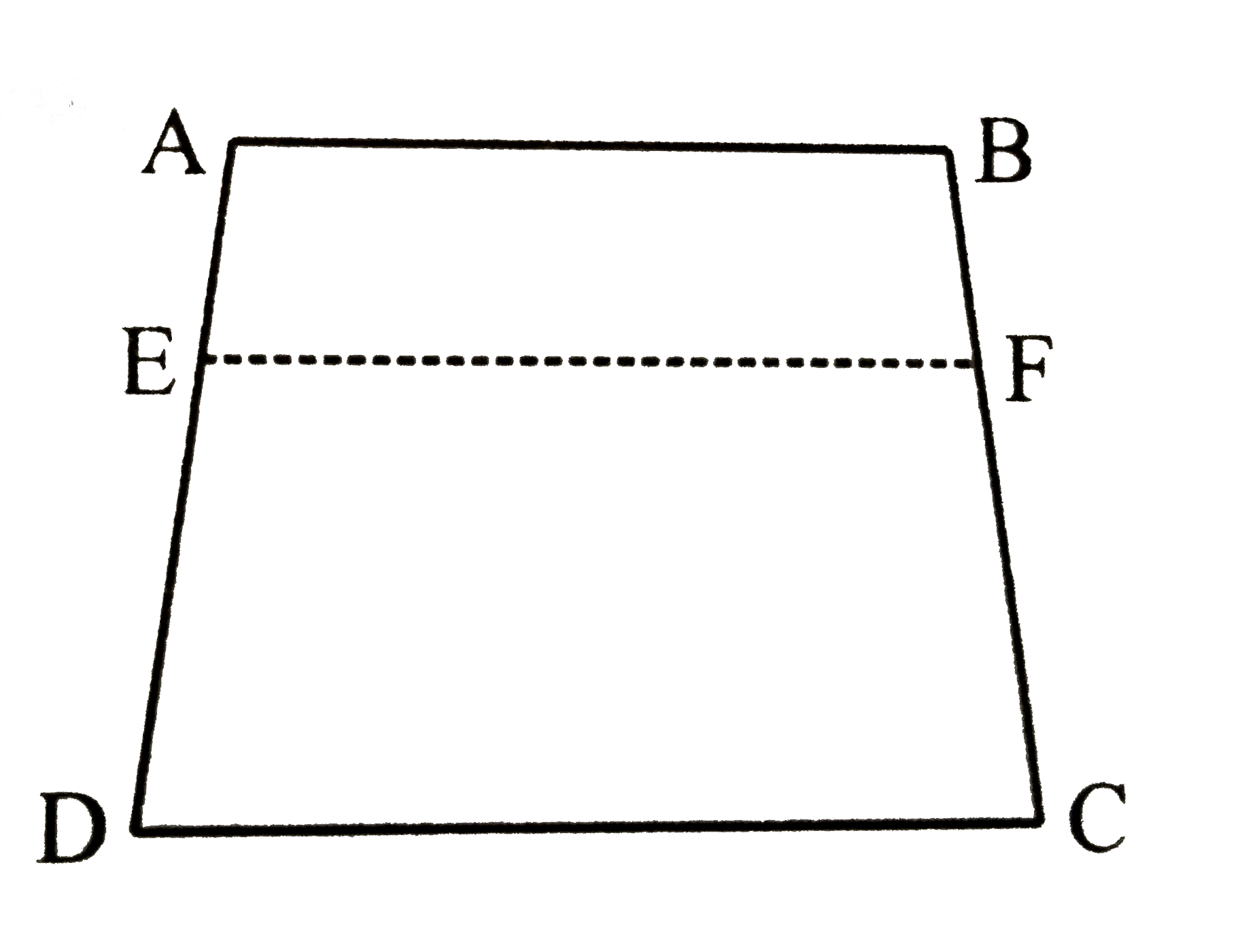
View Solutionचित्र में यदि EF||DC||AB हो, तो सिद्ध कीजिए की: AEED=BFFC
View SolutionIn trapezlum ABCD, AB || DC, E and F are points on non-parallel sides AD and BC respectively, such that EF || AB. Show that AEED=BFFC.
View SolutionIn trapezium ABCD, AB∣∣DC. E and F are points on non-parallel sides AD and BC respectively such that EF∣∣AB.
Show that AEED=BFFC.
View Solutionसमलम्ब चतुर्भुज ABCD में AB||DC है। AD व BC पर कर्मश: E और F इस प्रकार स्थित है की EF∣∣AB है। सिद्ध कीजिए| AEED=BFFC.
View Solutionசரிவகம் ABCD -யில் ,AB ||DC ,E மற்றும் F என்பன முறையே இணையற்ற பக்கங்கள் AD மற்றும் BC -யின் மீது அமைந்துள்ள புள்ளிகள் ,மேலும் EF ||AB என அமைந்தால் ,AEED =BFFC என நிறுவுக ?
View SolutionIn trapezium ABCD, AB∣∣DC. E and F are points on non-parallel sides AD and BC respectively such that EF∣∣AB.
Show that AEED=BFFC.
View SolutionIn trapezium ABCD, AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF || AB. Show that AEED=BFFC
View SolutionIn trapezium ABCD, AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF || AB. Show that AEED=BFFC
View SolutionIn trapezium ABCD, AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF || AB. Show that AEED=BFFC
View Solution
