ज्ञात कीजिए
बेलनाकार पेट्रोल की बंद टंकी की पार्श्व या वक्र पृष्ठीय क्षेत्रफल,जिसका व्यास है और ऊंचाई है|
(ii )इस टंकी को बनाने में कुल कितना इस्पात (steel ) लगा होगा, यदि कुल इस्पात भाग बनाने में नष्ट हो गया है?
प्रश्न में टंकी त्रिज्या
तथा टंकी की ऊंचाई
(i) टंकी का वक्रपृष्ठीय क्षेत्रफल
(iii) बंद टंकी का कुल पृष्ठीय क्षेत्रफल
माना की बेलनाकार टंकी बनवाने में प्रयोग की गई इस्पात का क्षेत्रफल
तो नष्ट हुए इस्पात का क्षेत्रफल
अतः प्रयोग में लाये गए इस्पात का क्षेत्रफल
समीकरण (i ) तथा (ii ) से,
Topper's Solved these Questions
- लम्ब वृतीय बेलन Book:KC SINHAChapter:लम्ब वृतीय बेलन Exercise:प्रश्नावली 16.2
Explore 36 Videos
- लम्ब वृतीय बेलन Book:KC SINHAChapter:लम्ब वृतीय बेलन Exercise:वस्तुनिष्ट प्रश्न
Explore 10 Videos
- रेखाएं और कोणBook:KC SINHAChapter:रेखाएं और कोणExercise:वस्तुनिष्ठ प्रश्न
Explore 9 Videos
- लम्ब वृत्तीय शंकु Book:KC SINHAChapter:लम्ब वृत्तीय शंकु Exercise:वस्तुनिष्ठ प्रश्न
Explore 7 Videos
Similar Questions
रिक्त स्थानों को भरें
(i) एक लम्ब वृतिये बेलन की त्रिज्या 7 cm और ऊंचाई 5 cm हो तो उसके पृष्ट का क्षेत्रफल ...........होगा|
(ii) एक लम्ब वृतीय बेलन की ऊंचाई 7 cm तथा आधार का व्यास 10m है तो बेलन का आयतन .........cm3 होगा|
(iii) एक लम्ब वृतीय बेलन का व्यास 7 cm तथा ऊंचाई 5 cm है तो बेलन का वक्र पृष्ट का क्षेत्रफल .............होगा|
View Solutionएक बेलन के आधार का व्यास 14 सेमी है और उसका वक्रपृष्ठ 1540 सेमी 2 है तो उसकी ऊंचाई है
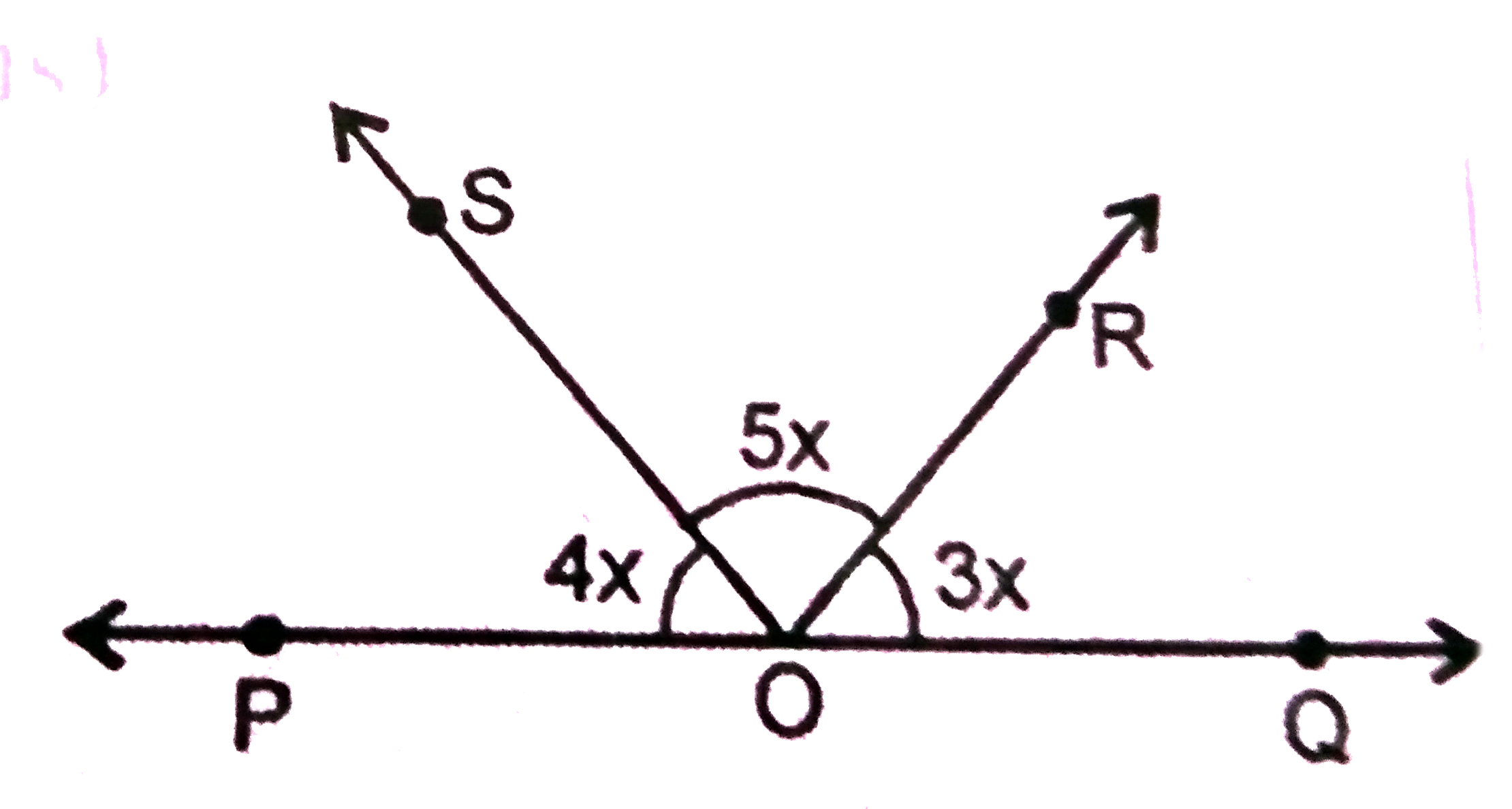
View Solutionबगल के चित्र में x बराबर है
View Solution24 मीटर ऊँचे शंकुकार तम्बू के आधार की परिधि 44 मीटर है। इस तम्बू को बनाने में प्रयुक्त कैनवास का क्षेत्रफल है :-
View Solution22 मी. × 20 मी. आयताकार छत से एक बेलनाकार पात्र जिसका व्यास 2 मी. तथा ऊंचाई 3.5 मी. है में पानी गिरता है। यदि पात्र पूरा भरा हुआ हो तब होई हुई वर्षा (सेमी. में) में ज्ञात करें?
View Solutionएक छोटी फर्म सोने के अंगूठियां और चेनों का निर्माण करती है| प्रतिदिन अंगूठियों और चेनों के निर्माण की कुल संख्या अधिकतम 24 है| एक अंगूठी बनाने में एक घंटा तथा के चेन के बनाने में 30 मिनट लगते है| प्रतिदिन उपलब्ध घंटों की अधिकतम संख्या 16 है|यदि अंगूठी पर लाभ रु 300 तथा एक चेन पर लाभ रु 190 हो, तो ज्ञात कीजिए| की प्रतिदिन कितनी अंगूठियों और चेनों का निर्माण किया जाय ताकि अधिकतम लाभ कमाया जा सकें|
View Solutionएक मोबाइल बनाने की कम्पनी में A और B ब्रांच में बनाये जाते है | कुल उत्पादन का 60 % ब्रांच A और ब्रांच B 40 % में बनाये जाते है | ब्रांच A में बने मोबाइल 2 % खराब पाए जाते है और ब्रांच B में बने मोबाइल 1 % खराब पाए जाते है।
यदि कुल बनाये गए मोबाइलों में किसी एक मोबाइल की जाँच की जाती है और मोबाइल को यादृच्छया निकलने पर खराब पाया जाता है तो उस मोबाइल का ब्रांच A में बनने में प्रायिकता ज्ञात कीजिए ।
View Solutionयह ज्ञात है की महाविद्यालय के छात्रों में से 60 % छात्रावास में रहते है और 40 % छात्रावास में नहीं रहते है । पूर्ववर्ती वर्ष से परिणाम सूचित करते है की छात्रावास में रहने वाले छात्रों में से30 % छात्रों में से 20 % छात्रों ने A ग्रेड लिए। वर्ष के अंत में महाविद्यालय के एक छात्र को यादृच्छया चुना गया और पाया गया की उसे A ग्रेड मिला है । इस बात की क्या प्रायिकता है की वह छात्रावास में रहने वाला है ?
View Solutionएक वृत्त का केंद्र (2x−1,3x+1) है। x ज्ञात कीजिए यदि वृत्त (-3,-1) में से गुजरे और व्यास की लम्बाई 20 मात्रक हो।
View SolutionA hemisphere is kept on top of a cube. Its front view is shown in the given figure the total height of the figure is 21cm. The ratio of curved surface area of hemisphere and total surface area of cube is 11 : 42. What is the total volume (in cm2) of figure?
एक अर्धगोला एक घन पर रखा गया है। इसके सामने का दृश्य आकृति में दर्शाया गया है। आकृति की कुल ऊँचाई 21 से.मी. हैं अर्धगोले के वक्र पृष्ठीय क्षेत्रफल तथा घन के कुल पृष्ठीय क्षेत्रफल का अनुपात 11 : 42 है। आकृति का कुल आयतन (से.मी.2 में) क्या है?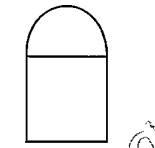
View SolutionA metallic hemispherical bowl is made up of steel. The total steel used in making the bowl is 342 pi cm^3, The bowl can hold 144 pi cm^3 water. What is the thickness (in cm) of bowl and the curved surface area (in cm^2 ) of outer side? इस्पात से धातु का एक अर्धगोलाकार कटोरा बनाया गया है। कटोरे को बनाने में कुल 342 pi से.मी.^3 इस्पात का प्रयोग किया गया है। कटोरा में 144 pi से.मी.^3 जल आ सकता है। कटोरे की मोटाई (से,मी. में) तथा बाहरी सतह का वक्र पृष्ठिय क्षेत्रफल ( से.मी.^2 में) क्या हें?
View SolutionBase of a right pyramid is a square of side 10 cm. If the height of the pyramid is 12 cm,then its total surface area is- एक लंब पिरामिड का आधार 10 सेमी भुजा का वर्ग है। यदि पिरामिड की ऊंचाई 12 सेमी है, तो कुल पृष्ठीय क्षेत्रफल कितना होगा?
View SolutionA pipe can fill a tank in 4 hours and a leak at the bottom can empty that full tank in 6 hours. If after the tank is 1/3 full, the leak is completely closed, how much time from beginning will it take for tank to get filled completely?
एक पाइप किसी टंकी को 4 घंटे में भर सकता है तथा तल पर मौजूद एक छिद्र इस भरी हुई टंकी को 6 घंटे में खाली कर सकता है | यदि टंकी के 1/3 भाग भर जाने के बाद इस छेद को पूरी तरह से बंद कर दिया जाता है, तो टंकी को पूर्णतः भरने में शुरू से कुल कितना समय लगेगा ?
View SolutionThe internal diameter of a hollow hemispherical vessel is 24 cm. It is made of a steel sheet which is 0.5 cm thick. What is the total surface area (in cm2) of the vessel ?
एक खोखले अर्धगोलीय बर्तन का आतंरिक व्यास 24 सेमी है | यह इस्पात की चादर से बना हुआ है जिसकी मोटाई 0.5 सेमी है | इस बर्तन का कुल पृष्ठ क्षेत्रफल ( वर्ग सेमी में) ज्ञात करें |
View SolutionThe length, breadth and height of a cuboid are 5 cm, 2 cm and 4 cm respectively. What is the total surface area of the cuboid?
किसी घनाभ की लंबाई, चौड़ाई और ऊंचाई क्रमशः 5 सेमी, 2 सेमी और 4 सेमी है | इस घनाभ का कुल पृष्ठीय क्षेत्रफल ज्ञात करें |
View Solutionगद्यांश में प्रयुक्त निम्नलिखित वाक्य को चार भागो में बाँटा गया है, जिनमे से किसी एक भाग में अशुद्धि है। अशुद्ध भाग को पहचानकर चिन्हित कीजिए।
View Solution