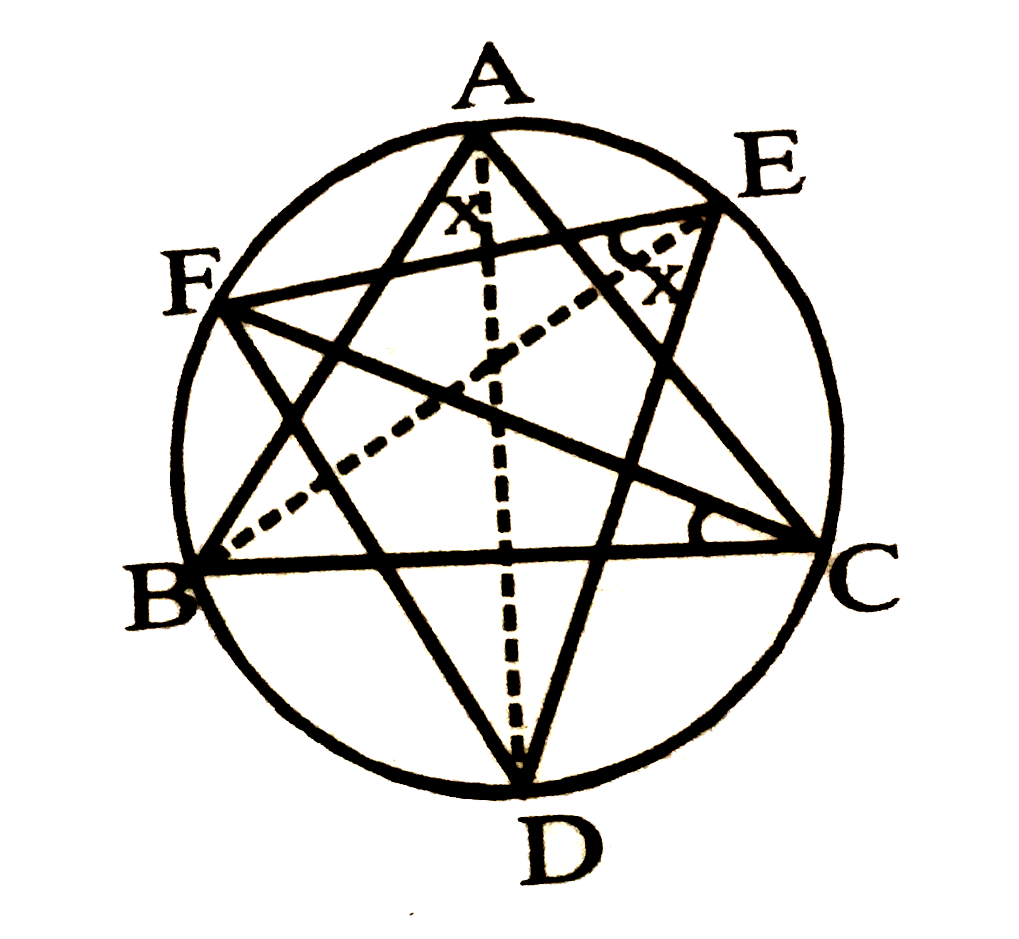
एक त्रिभुज ABC के कोणों A,B तथा C के समद्विभाजक उस त्रिभुज के परिवृत को क्रमशः बिन्दुओं D,E तथा F पर काटते है।
सिद्ध करे की ΔDEF के कोण 90∘−A2,90∘−B2−C2 है।
∠BED=∠BAD
(एक ही चाप पर स्थित है)
∠FEB=∠FCB
(एक ही चाप पर स्थित है)
∴∠BED+∠FEB=∠BAD+∠FCB
∴∠FED=12∠BAC+12∠ACB=12(∠BAC+∠ACB)
=12(180∘−∠ABC)=90∘−12∠ABC(−90B2)
इसी प्रकार ∠DEF=90∘−C2,∠FDE=90∘−A2
Topper's Solved these Questions
- वृत्त BOOK - KC SINHACHAPTER - वृत्त EXERCISE - EXERCISE 12.1 (अतिलघु उत्तरीय प्रश्न )
29 Videos
- वृत्त BOOK - KC SINHACHAPTER - वृत्त EXERCISE - EXERCISE 12.1 (लघु उत्तरीय प्रश्न )
5 Videos
- वास्तविक संख्याओं पर संक्रियाएँ एवं वास्तविक संख्याओं के घातांक BOOK - KC SINHACHAPTER - वास्तविक संख्याओं पर संक्रियाएँ एवं वास्तविक संख्याओं के घातांक EXERCISE - Objective Questions
30 Videos
- समांतर चतुर्भुजBOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - वस्तुनिष्ठ प्रश्न
9 Videos
Similar Questions
तीन अरैखिक बिन्दुओं से कितने वृत्त खींचे जा सकते है ।
View Solutionबगल के चित्र में O वृत्त के केन्द्र है ∠OBA=25∘ एवं ∠OCA=35∘ है, तो, ∠BAC ज्ञात करे।
View Solutionपरिमेय संख्या का दशमलव प्रसार कैसा होता है?
View Solutionचतुर्भुज के चारों कोणों का योग कितना समकोण होता है?
View Solutionयदि मूलबिंदु O के सापेक्ष त्रिभुज ABC के शीर्षों के स्थिति सदिश क्रमशः (1,−1,2),(2,1,3) और (−1,2,−1) है| तथा इसके केन्द्रक का स्थिति सदिश ज्ञात कीजिए|
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज के शीर्षो के निर्देशांक (2,5),(6−2) तथा (−3,−4) है , तो उसकी मध्यिकाओ के समीकरण ज्ञात कीजिए
View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionत्रिभुज ABC में कोण C समकोण है । यदि बिंदु A और B निर्देशांक क्रमशः (−3,4) और (3,−4)हो , तो सिद्ध कीजिये की ΔABC के परिवृत्त का समीकरण x2+y2=25 होगा ।
View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionसमाकलन के द्वारा त्रिभुज ABC का क्षेत्रफल ज्ञात कीजिए जिसके शीर्षो A, B तथा C के निर्देशांक क्रमश : (2,3), (4,7) तथा (6,2) है।
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View SolutionList - I List - II (A) बिन्दु (2, - 2), (- 2, 1) तथा (5, 2) (P) एक समकोणीय त्रिभुज के शीर्ष है (B) बिन्दु (1, - 2), (-3, 0) तथा (5, 6)(Q) एक समकोणीय समद्विबाहु त्रिभुज के शीर्ष है (C) बिन्दु (3,7), (6,5) तथा (15,-1)(R) एक समबाहु त्रिभुज के शीर्ष है (D) बिन्दु (2,2), (-2, -2) तथा (−2√3,2√3)(S) कोई त्रिभुज नहीं बनाते है
View Solutionदो रेखाओ के बीच कोण तथा त्रिभुज का अन्तःकोण
View Solution
