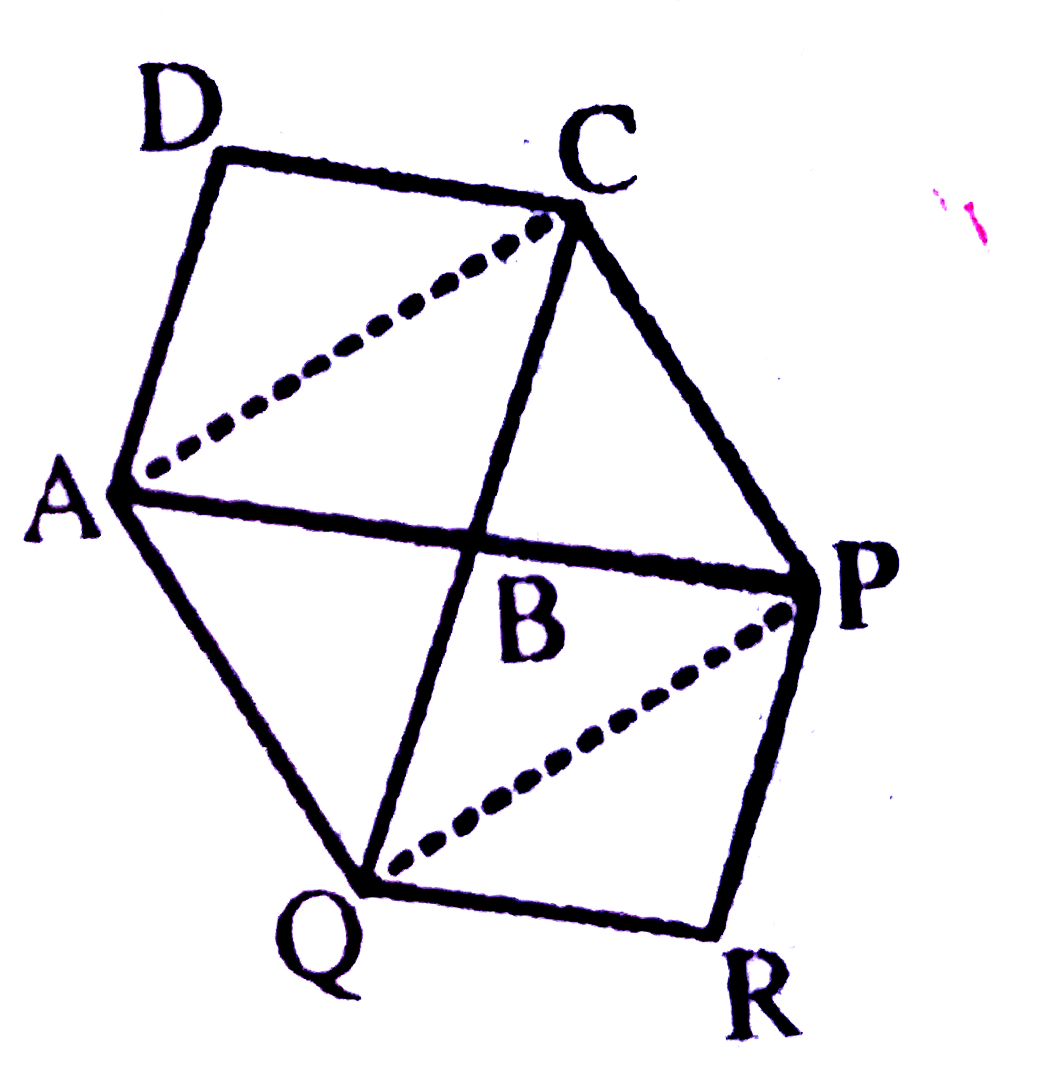
समांतर चतुर्भुज ABCD की एक भुजा AB को एक बिंदु P तक बढ़ाया गया है| A से होकर CP के समांतर खींची गई रेखा बढ़ाई गई CB से Q पर मिलती है और फिर समांतर चतुर्भुज PBQR को पूरा किया गया है (देखिये चित्र ) दर्शाइय की ar(ABCD)=ar(PBQR) है|
(##KCS_HIN_MAT_IX_C11_SLV_015_Q01.png" width="80%">
AC और QP को मिलाया
प्रमाण : ΔAQC और ΔAQP, दोनों त्रिभुज एक ही आधार AQ पर तथा एक ही समांतर रेखाओं AQ और CP (AQ∣∣CP दिया हुआ है) के बिच स्थित है
∴ ar(ΔAQC)=ar(ΔAQP) ...(i)
समीकरण (i ) में से दोनों तरफ ΔABQका क्षेत्रफल घटा देने से हमें मिलता है|
ar(ΔAQC)−ar(ΔAQB)=ar(ΔAQP)−ar(ΔAQB)
या ar(ΔABC)=ar(ΔQBP) या 2ar(ΔABC)=2ar(ΔQBP)
∴ ar(ABC)=ar(BQRP)
[∵ समांतर चतुर्भुज के कर्ण इसे दो बराबर त्रिभुजों में विभाजित करते है |]
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 11.1
24 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - वस्तुनिष्ट प्रश्न
7 Videos
- समांतर चतुर्भुजBOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - वस्तुनिष्ठ प्रश्न
9 Videos
- हीरोन का सूत्र BOOK - KC SINHACHAPTER - हीरोन का सूत्र EXERCISE - वस्तुनिष्ठ प्रश्न
13 Videos
Similar Questions
रिक्त स्थान को भरें :
(i) सर्वांगसम आयतों के क्षेत्रफल ...........होते है|
(ii) किसी समचतुर्भुज का क्षेत्रफल उसके विकर्णों की लम्बाइयों के गुणनफल का .....होता है
(iii) समलम्ब का क्षेत्रफल उसके समांतर भुजाओं के बीच की दुरी तथा समांतर भुजाओं के योग के गुणनफल का ......होता है|
(iv) सर्वांगसम त्रिभुजों के क्षेत्रफल ........होते है|
(v) एक ही आधार तथा एक ही समांतर रेखाओं के मध्य बने त्रिभुज क्षेत्रफल में ...........होते है|
View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
View Solutionचतुर्भुज के चारों कोणों का योग कितना समकोण होता है?
View Solutionयदि किसी ΔABC में BC=a,CA=b AB=c हो तो ΔABC की अर्धपरिमिति है
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionवृत्त के बाहर स्थित बिंदु से खींची गई स्पर्श रेखाओं की संख्या हो सकती है:
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionयदि बिंदु (4,6) से होकर जाने वाले मानक अतिपरवलय की उत्केंद्रता 2 है, तो (4,6) पर अतिपरवलय पर खींची गई स्पर्श रेखा का समीकरण है
View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionवक्र y=x2−5x+5 की स्पर्श रेखा, जो रेखा 2y=4x+1 के समांतर है, निम्न में से किस बिन्दु से होकर जाती है
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed . Show that ar (ABCD) = ar (PBQR)
View SolutionRevision|समांतर चतुर्भुज के गुण#!#Quiz की सहायता से Revision#!#परीक्षा की द्रष्टी से महत्वपूर्ण प्रश्न
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(∣∣gmABCD)=ar(∣∣gmPBQR)
View SolutionThe length of two sides of a parallelogram are 3cm and 10 cm. What is the sum of the squares of diagonals of the parallelogram ? एक समांतर चतुर्भुज के दो भुजाओं की लंबाई 3 सेमी और 10 सेमी है। समांतर चतुर्भुज के विकर्णों के वर्गों का योग क्या होगा ?
View Solution