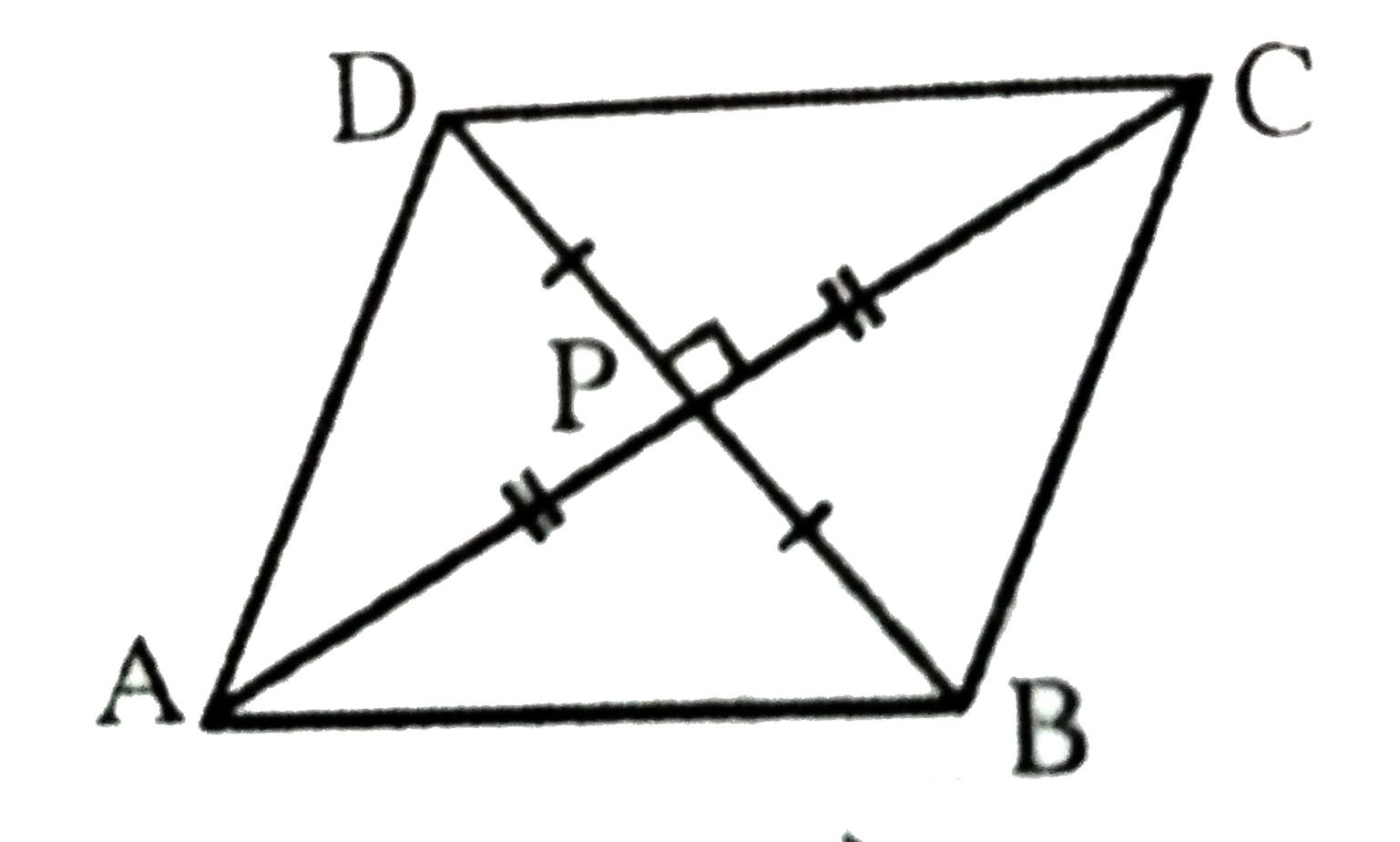
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें तो वह सक समचतुर्भुज होता है।
दिया है: एक चतुर्भुज ABCD जिसके विकर्ण एक –दूसरे को समकोण पर P बिंदु पर काटते हैं जिससे कि AP=PC,BP=PD तथा ∠DPC=∠DPA=∠APB=∠BPC=90∘
सिद्ध करना है: ABCD एक समचतुभुज है।
अर्थात AB=BC=CD=DA
प्रमाणः ΔAPD और ΔDPC में
दिया हुआ है AP=PC [हरेक =90∘]
DP=DP [उभ्यनिष्ठ]
∠APD=∠CPD [प्रत्येक =90∘]
∴ΔAPD≅ΔCPD[SAS सर्वांगसमता नियम से]
अतः AD=DC
इसी प्रकार यह दिखाया जा सकता है कि ΔAPD≅ΔAPB,ΔAPB≅ΔCPB
तथा ΔBPC≅ΔDPC
इस प्रकार यह भी दिखाया जा सकता है कि
AD=AB,AB=BC
तथा BC=CD
अतः AB=BC=CD=DA
अतः ABCD एक समचतुर्भुज है।
Topper's Solved these Questions
- समांतर चतुर्भुजBook:KC SINHAChapter:समांतर चतुर्भुजExercise:अतिलघु उत्तरीय प्रश्न (समांतर चमुर्भुज, आयत, वर्ग तथा समचतुर्भुज से संबंधित परिभाषाओं, प्रमेयों तथा उपप्रमेयों के सीधे प्रयोग पर आधारित प्रश्नः)
Explore 16 Videos
- समांतर चतुर्भुजBook:KC SINHAChapter:समांतर चतुर्भुजExercise:लघु उत्तरीय प्रश्न
Explore 4 Videos
- वृत्त Book:KC SINHAChapter:वृत्त Exercise:वस्तुनिष्ठ प्रश्न
Explore 17 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:KC SINHAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:वस्तुनिष्ट प्रश्न
Explore 7 Videos
Similar Questions
रिक्त स्थानों को भरें:
कोई समांतर चतुर्भुज एक समचतुर्भुज होगा यदि और केवल यदि उसके...................... एक-दूसरे पर लम्ब हो।
View Solutionकिसी समांतर चतुर्भुज ABCD में ∠D=110∘ तो ∠A एवं ∠B की माप अंशों में लिखें।
View Solutionवृत्त पर किन्ही दो बिन्दुओं को मिलाने वाली रेखाखंड को क्या कहते है ?
View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionदर्शाइए कि सदिश 2ˆi−ˆj+ˆk,ˆi−3ˆj−5ˆk और (3ˆi−4ˆj−5ˆk) एक समकोण त्रिभुज के शीर्षों कि रच्ना करते है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solutionयदि समान्तर चतुर्भुज कि दो आसान भुजाएँ →a तथा →b हो , तो इसका विकर्ण ज्ञात कीजिए।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionयदि दीर्घवृत्त 4x2+y2=8 के बिन्दुओ (1,2) तथा (a,b) पर खींची गई स्पर्श रेखाएं परस्पर लंबवत है, तो a2 बराबर है
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionमाना एक दीर्घवृत्त कि नाभियां S तथा S' है तथा इसके लघु अक्ष का कोई एक शीर्ष B है। यदि ΔS'BS एक समकोण त्रिभुज है जिसका समकोण B पर है तथा ΔS'BS का क्षेत्रफल 8 वर्ग इकाई है, तो दीर्घवृत्त की एक नाभिलम्ब जीवा की लम्बाई है
View Solutionदर्शाइए कि धनात्मक सम पूर्णांक 4q या 4q+2 के रूप का होता है, जहाँ एक पूर्णाक है।
View Solutionयदि दो समकोण त्रिभुजों में से एक त्रिभुज की एक भुजा और एक न्यूनकोण दूसरे त्रिभुज की एक भुजा और तदनुरूपी कोण के बराबर हो, तो दोनों त्रिभुज परस्पर क्या होंगे ?
View SolutionOne side of a rhombus is 6.5 cm and one of it’s diagonal is 12 cm. What is the area of the rhombus?
किसी समचतुर्भुज की एक भुजा 6.5 सेमी की है तथा इसका एक विकर्ण 12 सेमी का है | इस समचतुर्भुज का क्षेत्रफल ज्ञात करें |
View Solution