ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है | AP⊥BC खींच कर दर्शाइए कि ∠B=∠C है |
दिया है : ABC एक समद्विबाहु त्रिभुज है जिसमें तथा AB = AC
सिद्ध करना है कि : ∠B=∠C.
बनावट : AP⊥BC खींचा |
अब ΔAPB और ΔAPC में,
AB=AC [दिया है]
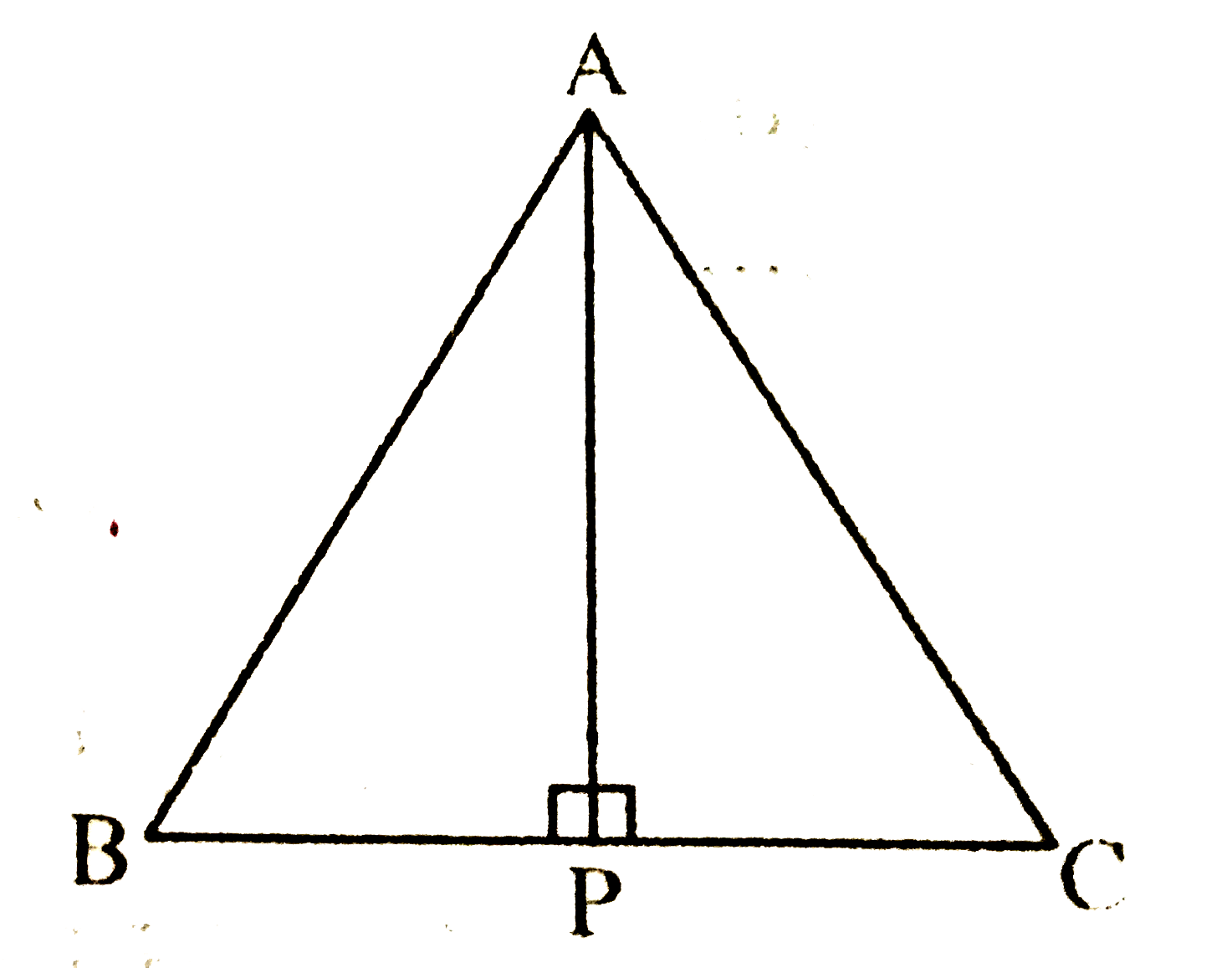
∠APB=∠APC=90∘
AP=AP [उभयनिष्ठ]
अत: ΔAPB≅ΔAPC [RHS नियम से]
∴ ∠ABP=∠ACP
अर्थात ∠B=∠C.
Topper's Solved these Questions
- त्रिभुजों की सर्वांगसमता BOOK - KC SINHACHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास 9.1 (अतिलघु उत्तरीय प्रश्न )
36 Videos
- त्रिभुजों की सर्वांगसमता BOOK - KC SINHACHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास 9.1 लघु उत्तरीय प्रश्न
11 Videos
- ज्यामितीय बनावट ( रचनाएँ ) BOOK - KC SINHACHAPTER - ज्यामितीय बनावट ( रचनाएँ ) EXERCISE - उदाहरण
11 Videos
- दो चरों वाले रैखिक समीकरण BOOK - KC SINHACHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - वस्तुनिष्ट प्रश्न
15 Videos
Similar Questions
यदि किसी त्रिभुज की दो भुजाएँ और उनके .............. कोण, दूसरे त्रिभुज की तदनुरूपी दोनों भुजाओं तथा उनके अंतर्गत कोण के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं |
View Solutionदो त्रिभुजों के सर्वांगसम होने के लिए भुजा-भुजा-भुजा प्रतिबंध को लिखें |
View Solutionएक △ABC बनाये जिसमे BC या (a) =6.6सेमि, CA+AB या (b+c) =10.2 सेमि तथा ∠B=60∘
View Solutionएकघातीय समीकरण ax+by+c=0 के वास्तविक हलो की संख्या है
View SolutionThe inverse of "if in a triangle ABC, AB = AC then ∠B=∠C" is
View SolutionThe contrapositive of "if in a triangle ABC, AB = AC then ∠B=∠C" is
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
View Solutionदर्शाइए कि सदिश 2ˆi−ˆj+ˆk,ˆi−3ˆj−5ˆk और (3ˆi−4ˆj−5ˆk) एक समकोण त्रिभुज के शीर्षों कि रच्ना करते है।
View Solutionएक ΔABC में, AB = ri + j, AC =si-j, यदि त्रिभुज का क्षेत्रफल इकाई परिमाण का है। तब,
View Solutionदर्शाइए कि धनात्मक सम पूर्णांक 4q या 4q+2 के रूप का होता है, जहाँ एक पूर्णाक है।
View SolutionIn triangle ABC, DE||BC where D is a point on AB and E is a point on AC. DE divides the area of triangle ABC into two equal parts.Then DB : AB is equal to एक त्रिभुज ABC DE||BC है जिसमें D,AB पर एक बिंदू है और E, AC पर एक बिंदू है। DE, triangle ABC के क्षेत्रफल को दो समान भागों में विभाजित करता है, DB : AB किसके बराबर हे?
View SolutionIn an isosceles triangle ABC, AB=AC and AD is perpendicular to BC at D. If AD = 8 cm and perimeter of triangle ABC is 64cm, then the area of triangle ABC एक समद्विबाहु त्रिभुज ABC में, AB= AC और AD, BC पर लंबवत है। यदि AD =8 सेमी और ABC की परिधि 64 cm है, तो ABC का क्षेत्रफल है:
View SolutionIn triangle ABC , D is a point on AC such that AB = BD = DC. If angle BAD=70^@ , then the measure of angle B is: त्रिभुज ABC में, D एक ऐसा बिंदु है कि AB = BD = DC है । यदि angle BAD=70^@ है, तो कोण B का मान ज्ञात करें |
View SolutionIn a triangle ABC , right angled at B, AB = 7 cm and (AC - BC) = 1 cm. The value of (secC + cotA) is : त्रिभुज ABC में, जिसमें B समकोण है, AB = 7 सेमी और (AC - BC) = 1 सेमी है| (secC + cotA) का मान ज्ञात करें|
View SolutionIn triangle ABC , D is a point on side AB, such that, BD = 2cm and DA = 3cm. E is a point on BC such that DE || AC and AC = 4 cm. Then (Area of triangle BDE ): (Area of trapezium ACED) is: त्रिभुज ABC में, D, भुजा AB पर स्थित ऐसा बिंदु है कि BD = 2 सेमी और DA =3 सेमी है | E, BC पर स्थित ऐसा बिंदु है कि DE || AC है और AC =4 सेमी है | तो त्रिभुज (BDE का क्षेत्रफल ) : (समलम्ब ACED का क्षेत्रफल) ज्ञात करें |
View Solution
