नीचे के चित्र में ΔPQR की भुजा QR को S बिंदु तक बढ़ाया गया है । यदि ∠PQR और ∠PRS के समद्विभाजक बिंदु T पर मिलते हैं तो सिद्ध कीजिए कि ∠QTR=12∠QPR है।
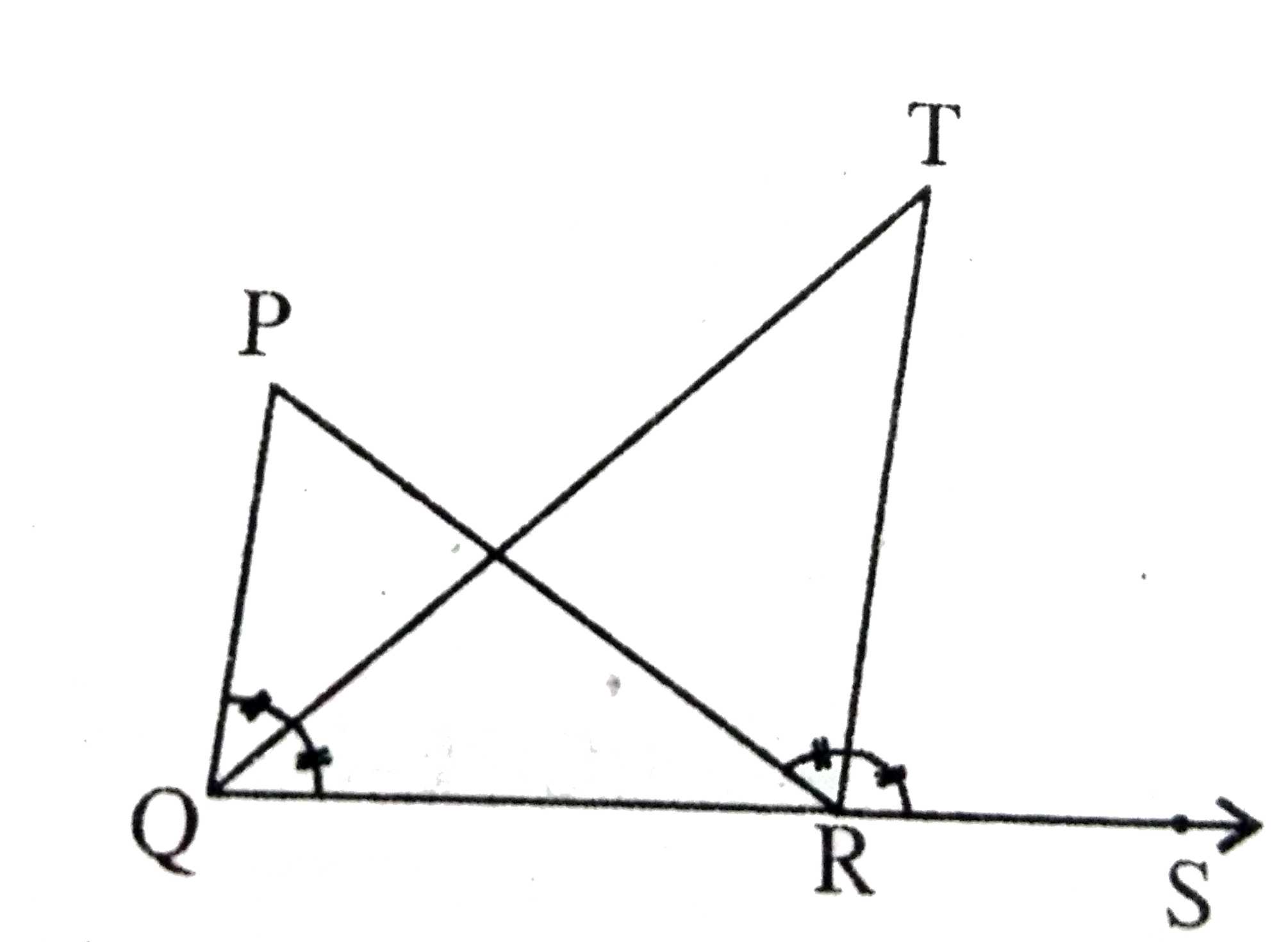
माना कि ∠QPR=x,∠PQR=y तथा ∠PRQ=z
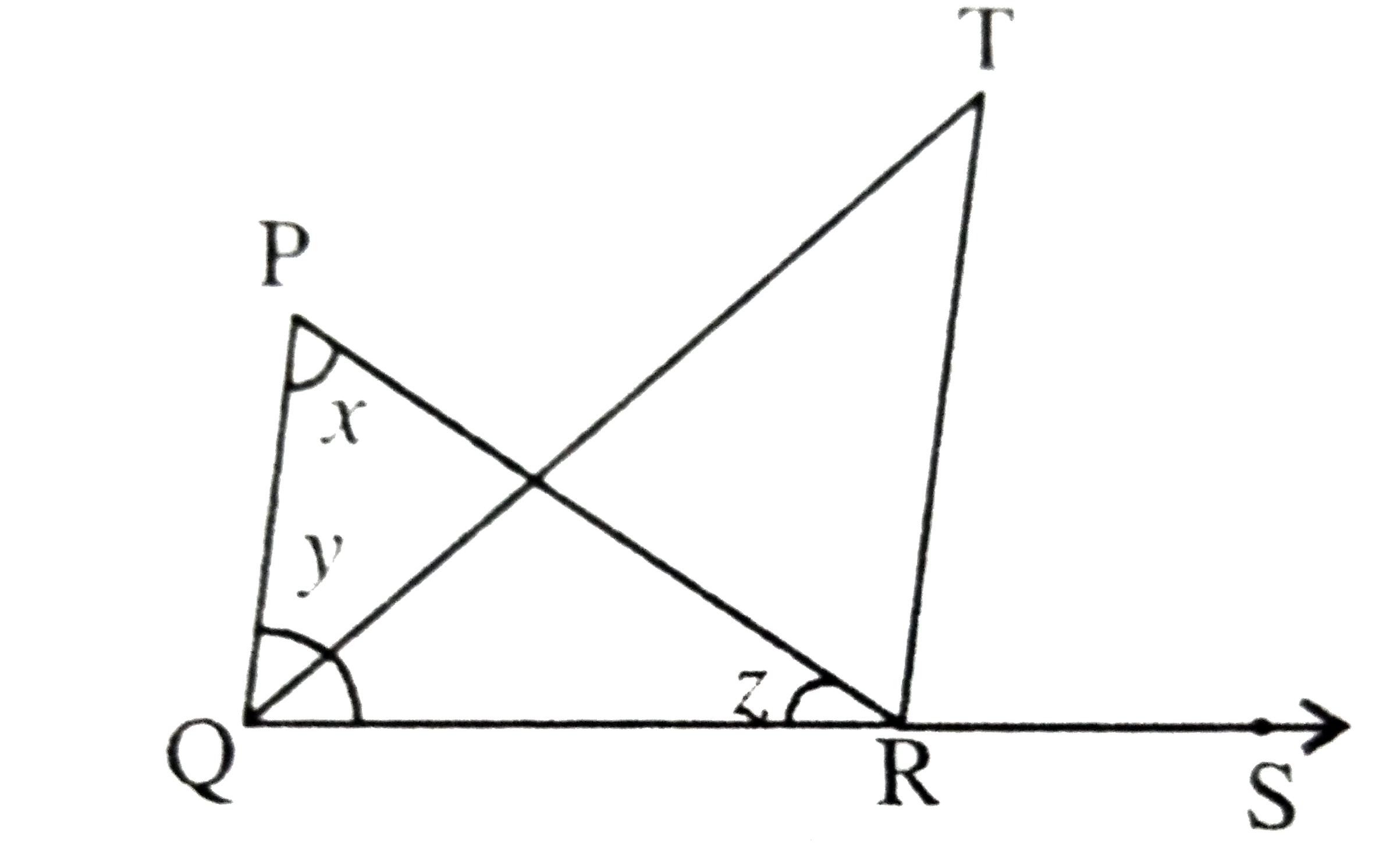
∵QT,∠PQR को समद्विभाजित करता है। ∴∠TQR=12(y)=y2
चूंकि बहिष्कोण सामने के दोनों अंतः कोणों के योग के बराबर होता है
∴∠PRS=x+y,
∴∠PRT=12∠PRS [ ∵RT,∠PRS को समद्विभाजित करता है।]
=12(x+y)=12(180∘−z)∵x+y+z=180∘ [त्रिभुज के तीनों कोणों का योग]
=90∘−12z
अब ΔTQR में ∠TQR+∠QRT+∠QTR=180∘ [त्रिभुज के तीनों कोणों का योग]
या 12y+(z+∠PRT)+∠QTR=180∘
या 12y+{z+(90∘−12z)}+∠QTR=180∘
या 12y+(90∘+12z)+∠QTR=180∘
या (12y+12z)+90∘+∠QTR=180∘
या 12(y+z)+∠QTR=180∘−90∘−90∘
या 12(180∘−x)+∠QTR=90∘
या (90∘−x2)+∠QTR=90∘
अतः ∠QTR=x2=12∠QPR
Topper's Solved these Questions
- रेखाएं और कोणBOOK - KC SINHACHAPTER - रेखाएं और कोणEXERCISE - अति लघु उत्तरीय प्रश्न ( रिक्त स्थानों को भरें ताकि दिया गया कथन सत्य हो।)
5 Videos
- रेखाएं और कोणBOOK - KC SINHACHAPTER - रेखाएं और कोणEXERCISE - अति लघु उत्तरीय प्रश्न (निम्नलिखित कथनों में कौन सत्य है तथा कौन असत्य है लिखें।)
5 Videos
- यूक्लिड की ज्यामितीय का परिचय BOOK - KC SINHACHAPTER - यूक्लिड की ज्यामितीय का परिचय EXERCISE - वस्तुनिष्ठ प्रश्न
15 Videos
- लम्ब वृतीय बेलन BOOK - KC SINHACHAPTER - लम्ब वृतीय बेलन EXERCISE - वस्तुनिष्ट प्रश्न
10 Videos
Similar Questions
तल में दो भिन्न बिंदुएं एक ................................ रेखा को निर्धारित करते हैं।
View Solutionरैखिक युग्म को बनाने वाले दोनों कोण न्यूनकोण होते हैं।
View Solutionएक बिंदु से होकर कितनी रेखाएँ खींची जा सकती हैं ?
View Solutionएक बेलन के आधार का व्यास 14 सेमी है और उसका वक्रपृष्ठ 1540 सेमी 2 है तो उसकी ऊंचाई है
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
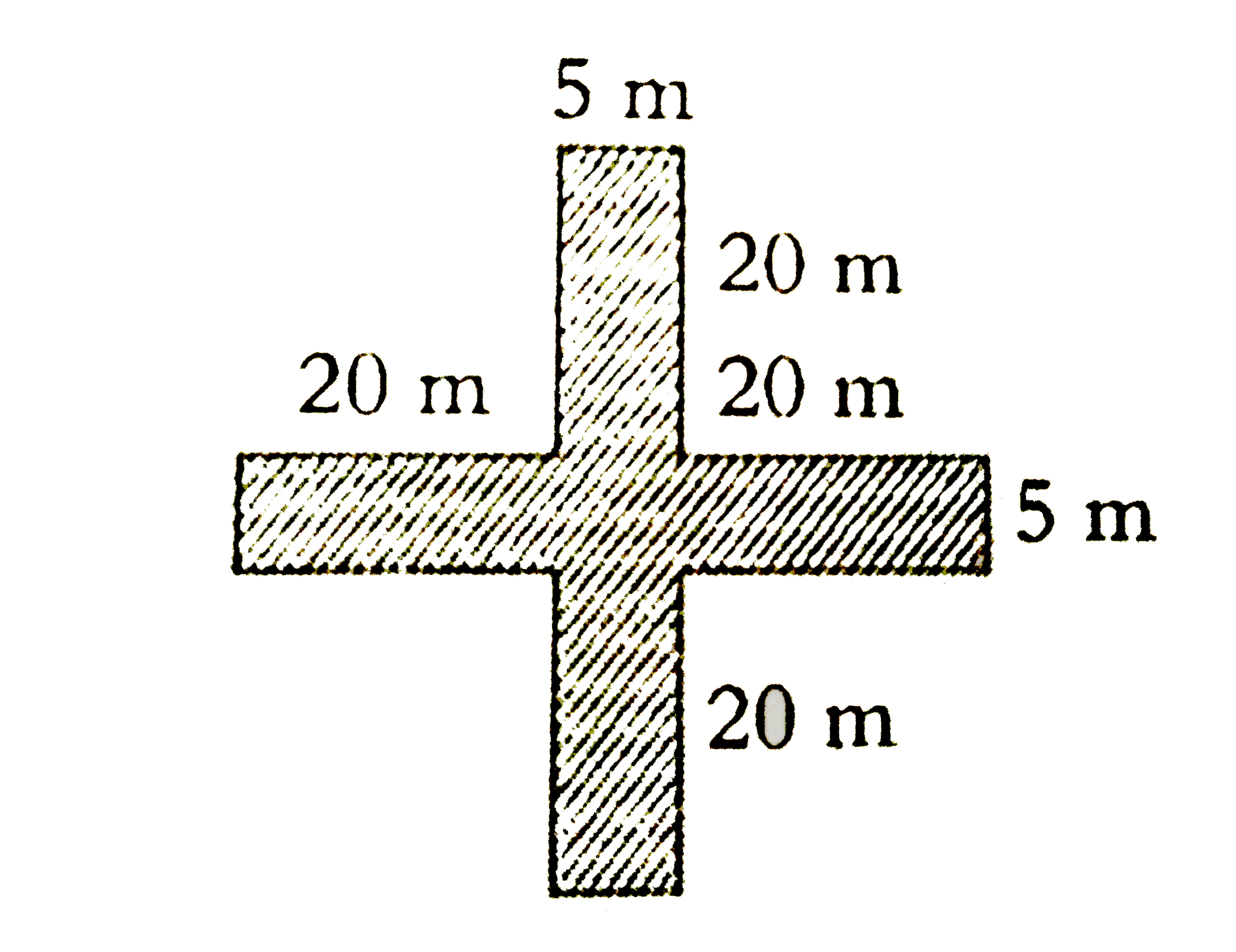
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View Solution
