निम्नलिखित में से प्रत्येक का गुणनखंड कीजिए :
27p3−1216−92p2+14p
दिया गया व्यंजक
27p3−1216−92p2+14p
=(3p)3+(−16)3+3x3(3p)(−16){3p+(−16)}
={3p+(−16)}3=(3p−16)3
=(3p−16)(3p−16)(3p−16)
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - बीजीय सर्वसमिकाएँEXERCISE - साधित उदाहरण19videos
बीजीय सर्वसमिकाएँ
- BOOK - KC SINHACHAPTER - बीजीय सर्वसमिकाएँEXERCISE - अभ्यास -4.123videos
बीजीय सर्वसमिकाएँ
- BOOK - KC SINHACHAPTER - प्रायिकता या सम्भावितEXERCISE - दीर्घ उत्तरीय प्रश्न3videos
प्रायिकता या सम्भावित
- BOOK - KC SINHACHAPTER - यूक्लिड की ज्यामितीय का परिचय EXERCISE - वस्तुनिष्ठ प्रश्न15videos
यूक्लिड की ज्यामितीय का परिचय
Similar Questions
निम्नलिखित में से प्रत्येक का गुणनखंड कीजिए
27y3+125z301:34View Solutionउपयुक्त सर्वसमिकाओ का उपयोग कर निम्नलिखित गुणनफल ज्ञात कीजिए:
(x+3)(x+3)04:51View Solution70 विद्यार्थी के प्राप्ताकों का विवरण नीचे तालिका में दिया गया है।
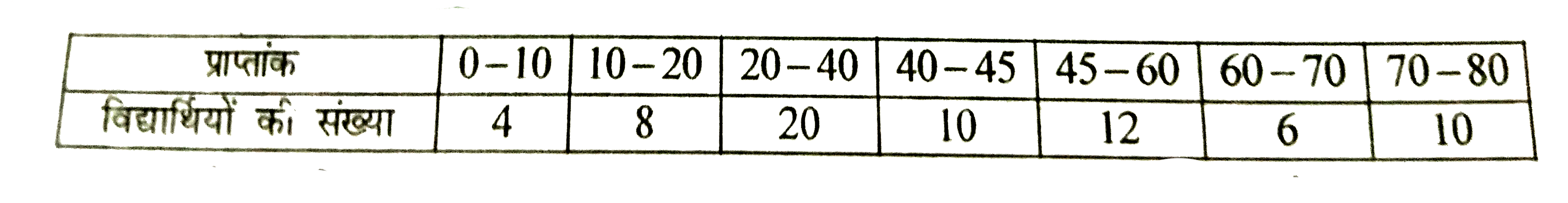
एक विद्यार्थी द्वारा निम्नलिखित वर्ग-अन्तराओं के बीच प्राप्तांकों की प्रायिकता ज्ञात करें।
(i) 0-20 (ii) 0-6002:32View Solutionएक बिंदु से होकर कितनी रेखाएँ खींची जा सकती हैं ?
02:35View SolutionFactorize: 27 p3−1216−92p2+14p
02:25View SolutionFactorise
(i)8p3+125p2+625p+1125
(ii)27p3−92p2+14p−121602:17View Solutionनिम्न व्यंजको के गुणनखण्ड करो:
27p3−1216−92p2+14p03:14View Solutionनिम्नलिखित में से प्रत्येक का मान xp के q वें मूल के रूप में अर्थात सूत्र xpq=(xp)1q का प्रयोग करते हुए ज्ञात कीजिए :
(6254096)3402:08View Solutionनिम्नलिखित में से प्रत्येक का मान xp के q वें मूल के रूप में अर्थात सूत्र xpq=(xp)1q का प्रयोग करते हुए ज्ञात कीजिए :
(121289)3203:21View Solutionनिम्नलिखित में से प्रत्येक का मान xp के q वें मूल के रूप में अर्थात सूत्र xpq=(xp)1q का प्रयोग करते हुए ज्ञात कीजिए :
(5904916807)2503:38View Solutionनिम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए :
(0.008)4303:36View Solutionनिम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए :
6412×(6412+1)03:24View Solutionनिम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए :
27−13×(2713−2723)02:44View Solutionनिम्नलिखित प्रत्येक समीकरण को हल कीजिए :
3+2x=6412+271301:28View SolutionFactorize the following. (i) 27P^3 - (1/216) - (9/2)P^2 + (1/4)P
03:11View SolutionFactorize: 27 p3−1216−92p2+14p
01:21View Solution