If two protons are moving with speed $v = 4.5 \times 10^{5} m / s$ parallel to each other then find the ratio of electrostatic and magnetic force between them : -

A

$4.4 \times 10^{5}$

B

$2.2 \times 10^{5}$

C

$3.3 \times 10^{5}$

D

$1.1 \times 10^{5}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

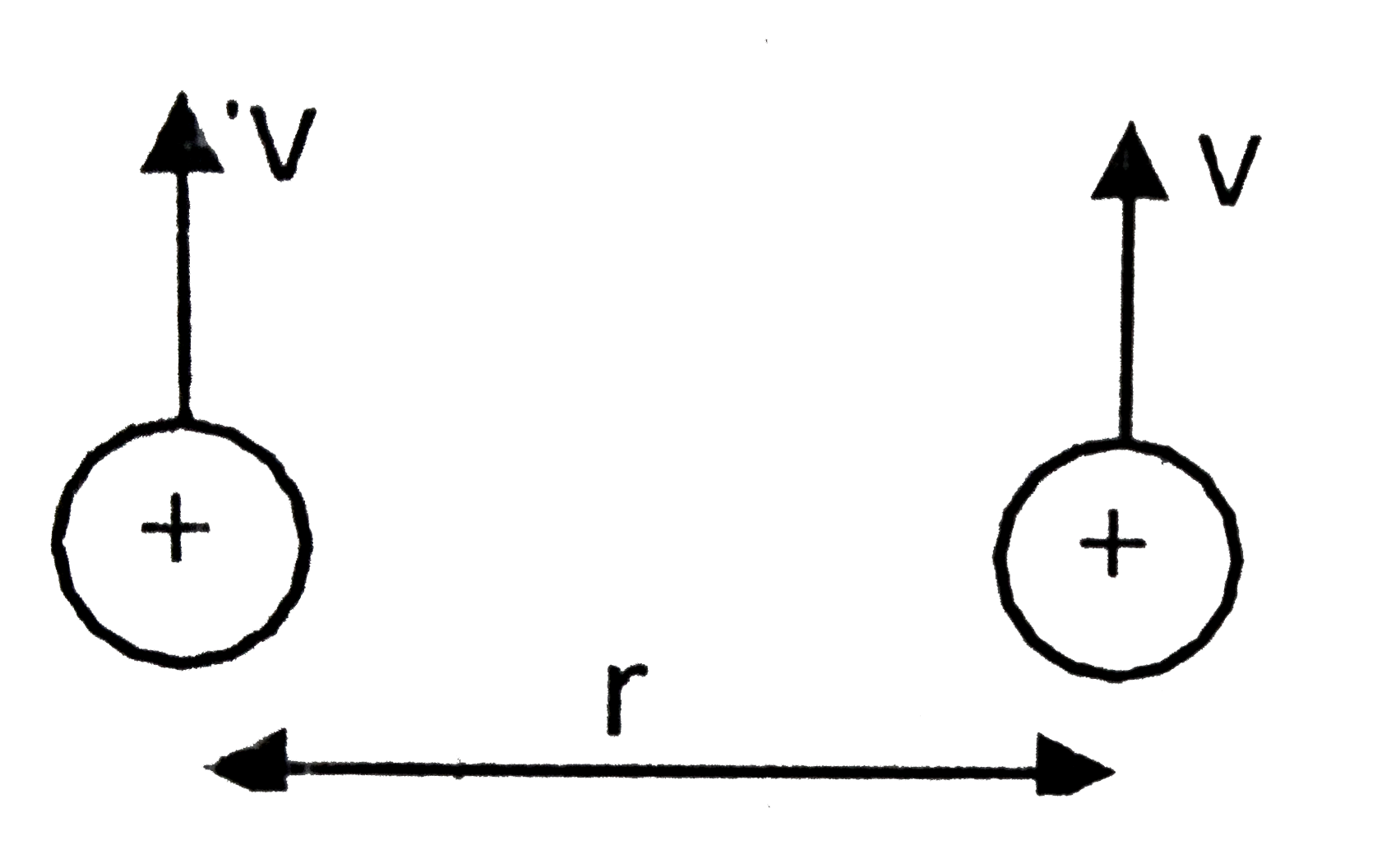
$F_{E} = \frac{k e^{2}}{r^{2}}$
$F_{M} = e V B = e . V . \frac{μ_{0}}{4 π} . \frac{e V}{r^{2}}$
$\frac{F_{E}}{F_{M}} = \frac{\frac{k e^{2}}{r^{2}}}{\frac{e^{2} V^{2} . μ_{0}}{4 π r^{2}}} = \frac{k .4 π}{V^{2} . μ_{0}}$
$= \frac{9 \times 10^{9} \times 4 π}{4.5 \times 4.5 \times 10^{10} \times 4 π \times 10^{- 7}} = \frac{9 \times 10^{6}}{4.5 \times 4.5} = 4.4 \times 10^{5}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two electrons are moving with speed of $5 \times 10^{5}$ m/s parallel to each other, then the electrostatic and magnetic force between them is
A $5 \times 10^{5}$
B $2.5 \times 10^{4}$
C $3.6 \times 10^{5}$
D $4.4 \times 10^{3}$
Question 2 - Select One
Two electrons move parallel to each other with equal speed $' V'$ the ratio of magnetic $&$ electric force between them is
A $V / C$
B $C / V$
C $V^{2} / C^{2}$
D $C^{2} / V^{2}$
Question 3 - Select One
Two electrons move parallel to each other with equal speed $' V'$ the ratio of magnetic $&$ electric force between them is
A $\sqrt{\frac{v}{c}}$
B ${(\frac{c}{v})}^{2}$
C ${(\frac{v}{c})}^{2}$
D $\sqrt{\frac{c}{v}}$

AIIMS PREVIOUS YEAR PAPERS-AIIMS 2019 25 MAY EVENING SHIFT-PHYSICS

Home
Ask Doubt
Profile