The molar specific heat of a gas as given from the kinetic theory is 52R. If it is not specified whether it is CporCυ one could conclude that the molecules of the gas
are definitely monoatomic
are definitely regid diatomic
are definited non - rigid diatmic
can be monoatomic or rigid diatomic
The correct Answer is:D
Step by step video, text & image solution for The molar specific heat of a gas as given from the kinetic theory is (5)/(2) R. If it is not specified whether it is C_(p) or C_(upsilon) one could conclude that the molecules of the gas by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
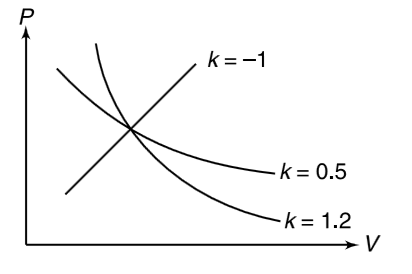
Figure shows P versus V graph for various processes performed by an ideal gas. All the processes are polytropic following the process equation PVk= constant.
(i) Find the value of k for which the molar specific heat of the gas for the process is CP+CV2. Does any of the graph given in figure represent this process?
(ii) Find the value of k for which the molar specific heat of the gas is CV+CP. Assume that gas is mono atomic. Draw approximately the P versus V graph for this process in the graph given above.
View SolutionIf γ be the ratio of specific heats (Cp&Cv) for a perfect gas. Find the number of degrees of freedom of a molecules of the gas?
View Solution
Knowledge Check
Molar specific heat at constant volume Cv for a monatomic gas is
A32RB52RC3RD2RIf the molar specific heat of a gas at constant pressure is 72R, then the atomicity of gas is
AoneBtwoCthreeDfourThe molar specific heat at constant volume of gas mixture is 13R6. The gas mixture consists of
A2 moles of O2 and 4 moles of H2B2 moles of O2 and 4 moles of argonC2 moles of argon and 4 moles of O2D2 moles of CO2 and 4 moles of argon
The molar specific heat at constant pressure of an ideal gas is 72R. The gas is made up of molecules which are
View SolutionThe ratio of the specific heats of a gas is CpCv=1.66 then the gas may be
View SolutionThe ratio of specific heats of a gas is 1.4. if the value of CV is 20.8 J/mol K, then the CP is
View SolutionThe molar specific heats of an ideal gas at constant pressure and volume are denotes by CP and Cυ respectively. If γ=CPCυ and R is the universal gas constant, then Cυ is equal to
View SolutionThe ratio of the specific heats CPCυ=γ in terms of degrees of freedom is given by
View Solution

