Black holes in orbit around a normal star are detected from the earth due to the fricitional heating of infalling gas into the black hole, which can reach temperature greater than 106K. Assuming that the infalling gas can be modelled as a blackbody radiator, then the wavelenght of maximum power lies
in the visible region
in the X-ray region
in the microwave region
in the gamma-ray region of electromagnetic spectruem
The correct Answer is:B
λmT=2.9×10−3106=2.9×10−9m=2.9nm. It lies in the
X-ray region of the electromagnetic spectrum.
Topper's Solved these Questions
Similar Questions
Answer the following: (a) You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means? (b) An astronaut inside a small spaceship orbiting around the Earth cannot detect gravity. If the space station orbiting around the Earth has a large size, can he hope to detect gravity? (c) If you compare the gravitational force on the Earth due to the Sun to that due to the Moon, you would find that the Sun’s pull is greater than the Moon’s pull. (You can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the Moon’s pull is greater than the tidal effect of Sun. Why?
View SolutionAnswer the following: (a) You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means? (b) An astronaut inside a small spaceship orbiting around the Earth cannot detect gravity. If the space station orbiting around the Earth has a large size, can he hope to detect gravity? (c) If you compare the gravitational force on the Earth due to the Sun to that due to the Moon, you would find that the Sun’s pull is greater than the Moon’s pull. (You can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the Moon’s pull is greater than the tidal effect of Sun. Why?
View Solution
Knowledge Check
Two stars bound together by gravity orbit othe because of their mutual attraction. Such a pair of stars is referred to as a binary star system. One type of binary system is that of a black hole and a companion star. The black hole is a star that has cullapsed on itself and is so missive that not even light rays can escape its gravitational pull therefore when describing the relative motion of a black hole and companion star, the motion of the black hole can be assumed negligible compared to that of the companion.
The orbit of the companion star is either elliptical with the black hole at one of the foci or circular with the black hole at the centre. The gravitational potential energy is given by U=−GmM/r where G is the universal gravitational constant, m is the mass of the companion star, M is the mass of the black hole, and r is the distance between the centre of the companion star and the centre of the black hole. Since the gravitational force is conservative. The companion star and the centre of the black hole, since the gravitational force is conservative the companion star's total mechanical energy is a constant. Because of the periodic nature of of orbit there is a simple relation between the average kinetic energy <K> of the companion star Two special points along the orbit are single out by astronomers. Parigee isthe point at which the companion star is closest to the black hole, and apogee is the point at which is the farthest from the black hole.
Q. Which of the following prevents the companion star from leaving its orbit and falling the black hole?AThe centripetal forceBthe gravitational forceCThe companion star's potential energyDThe companion star's kinetc energyTwo stars bound together by gravity orbit othe because of their mutual attraction. Such a pair of stars is referred to as a binary star system. One type of binary system is that of a black hole and a companion star. The black hole is a star that has cullapsed on itself and is so missive that not even light rays can escape its gravitational pull therefore when describing the relative motion of a black hole and companion star, the motion of the black hole can be assumed negligible compared to that of the companion.
The orbit of the companion star is either elliptical with the black hole at one of the foci or circular with the black hole at the centre. The gravitational potential energy is given by U=−GmM/r where G is the universal gravitational constant, m is the mass of the companion star, M is the mass of the black hole, and r is the distance between the centre of the companion star and the centre of the black hole. Since the gravitational force is conservative. The companion star and the centre of the black hole, since the gravitational force is conservative the companion star's total mechanical energy is a constant. Because of the periodic nature of of orbit there is a simple relation between the average kinetic energy <K> of the companion star Two special points along the orbit are single out by astronomers. Parigee isthe point at which the companion star is closest to the black hole, and apogee is the point at which is the farthest from the black hole.
Q. For circular orbits the potential energy of the companion star is constant throughout the orbit. if the radius of the orbit doubles, what is the new value of the velocity of the companion star?Ait is 1/2 of the old valueBit is 1/√2 of the old valueCit is the same as old valueDit is double the old valueA particular star (assuming it as a black body) has a surface temperature of about 5×104K The wave length in nano-meters at which its radiation becomes maximum is (b=0.0029mk) .
A48B58C60D70
A steel plate is 0.3m long, 0.1m wide and 0.012m thick. The plate is placed on a heating plate of identical size maintained at 100∘C. The heating plate is receiving energy through a 50 W heater. The heating plate losses heat only to the steel plate which is well insulated from all sides except at the top. The top surface of the steel plate is exposed to an airstream of temperature 20∘C. The top surface of the steel plate radiates like a black body. Calculate the rate at which the top surface looses heat due to convection. The surface of steel plate in contact with heating plate is at 100∘C. Thermal conductivity of steel k=16Wm−1K−1 Stefan’s constant =5.67×10−8Wm−2K−4
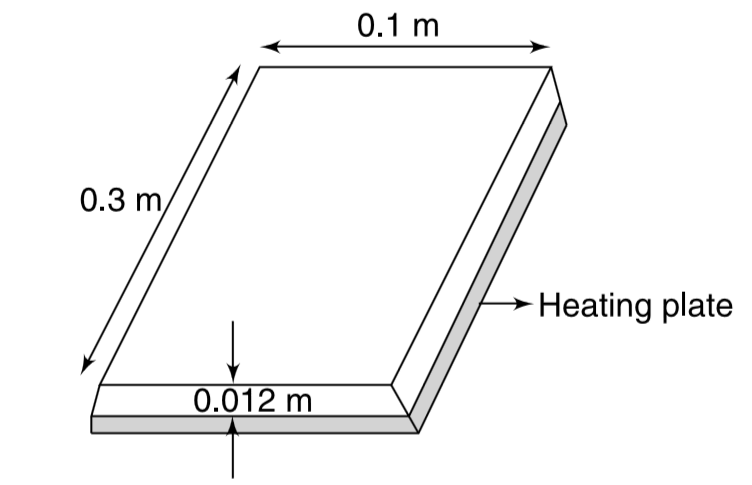
View SolutionAccording to stefan's law of radiation a black body radiates energy σT4 from is unit surface area every second where T is the surface temperature of the black body and σ=5.67×10−8W/m2K4 is known as Stefan's of as a ball of radius 0.5m When detonated it reaches temperature of 106K and can be treated as a black body Estimate the power it radiates .
View SolutionA silver ball painted black is kept inside a box which is maintained at a temprature of 27∘C the ball is maintained initially at a constant temperature of 127∘C by making the radiation to fall on it through a small hole in the box latter on due to some chemical reaction between silver and paint the paint uniformly evaporates from the surface of ball exposing the silver if same amount of radiation continues to fall on ball then temperature of ball as a function of time is hown as :(Assume emissivity of silver is zero and paint to be black body also assume radiation to be the only mode of heat transfer)

View SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK. Standard vapour pressures of A and B are P0A and P0B, respectively, at TK. We collect the vapour of A and B in two containers of volume V, first container is maintained at 2TK and second container is maintained at 3T/2. At the temperature greater than TK, both A and B exist in only gaseous form.
We assume than collected gases behave ideally at 2TK and there may take place an isomerisation reaction in which A gets converted into B by first-order kinetics reaction given as:
Ak−−→B, where k is a rate constant.
In container (II) at the given temperature 3T/2, A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

r=K.P√M0
where P= pressure differences between system and surrounding
K= positive constant
M0= molecular weight of the gas
If vapours are collected in a container of volume 8.21L maintained at 3T/2K, where T=50K, then the ratio of initial rate of effusion of gases A and B is given as
View SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK. Standard vapour pressures of A and B are P0A and P0B, respectively, at TK. We collect the vapour of A and B in two containers of volume V, first container is maintained at 2TK and second container is maintained at 3T/2. At the temperature greater than TK, both A and B exist in only gaseous form.
We assume than collected gases behave ideally at 2TK and there may take place an isomerisation reaction in which A gets converted into B by first-order kinetics reaction given as:
Ak−−→B, where k is a rate constant.
In container (II) at the given temperature 3T/2, A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

r=K.P√M0
where P= pressure differences between system and surrounding
K= positive constant
M0= molecular weight of the gas
If partial vapour pressure of A is twice that of partial vapour pressure of B and total vapour pressure 2 atm at TK, where T=50K and V=8.21L, then the number of moles of A and B in vapour phase is:
View Solution

