A strone thrown into still water, creates a circular wave pattern moving radially outwards. If r is the distance measured from the centre of the pattern. The amplitudeof the aves varies as
r−1/2
r−1
r−2
r3/2
The correct Answer is:A
For circular wave, intensity I∝1r.
Amplitude A∝√I,a∝√1ror,A∝r−1/2
Topper's Solved these Questions
Similar Questions
A star like the sun has serveral bodies moving around it at different distance. Consider that all of them are moving in circular orbits. Let r be the distance of the body from the centre of the star and let its linear velocity be υ, angular velocity ω, kinetic energy K, gravitational potential energy U, total energy E and angular momentum L. As the radius r of the orbit increase, determine which of the above quantities increase and which ones decrease.
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium distance is given by
View Solution
Knowledge Check
In Young's double slit experiment, the 10th maximum of wavelength λ1 is at a distance y1 from its central maximum and the 5th maximum of wavelength λ2 is at a distance y2 from its central maximum. The ratio y1/y2 will be
A2λ1λ2B2λ2λ1Cλ12λ2Dλ12λ1In a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The work required to move the particle from equilibrium distance to infinity isAB4AB4BACB24AD4B2AIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
If the total energy of the particle is E=−3B216A, and it is known that the motion is radial only then the velocity is zero atAr03B2r03Cr0D2r05
In a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium is
View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View SolutionA uniform but time-varying magnetic field B (t) exists in a circular region of radius a and is directed into the plane of the paper as shown . The magnitude of the induced electric field at point P at a distance r from the centre of the circular region is
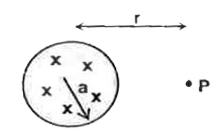
View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View Solution

