Two spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is

12π√km
12π√2km
12π√3km
12π√mk
The correct Answer is:C
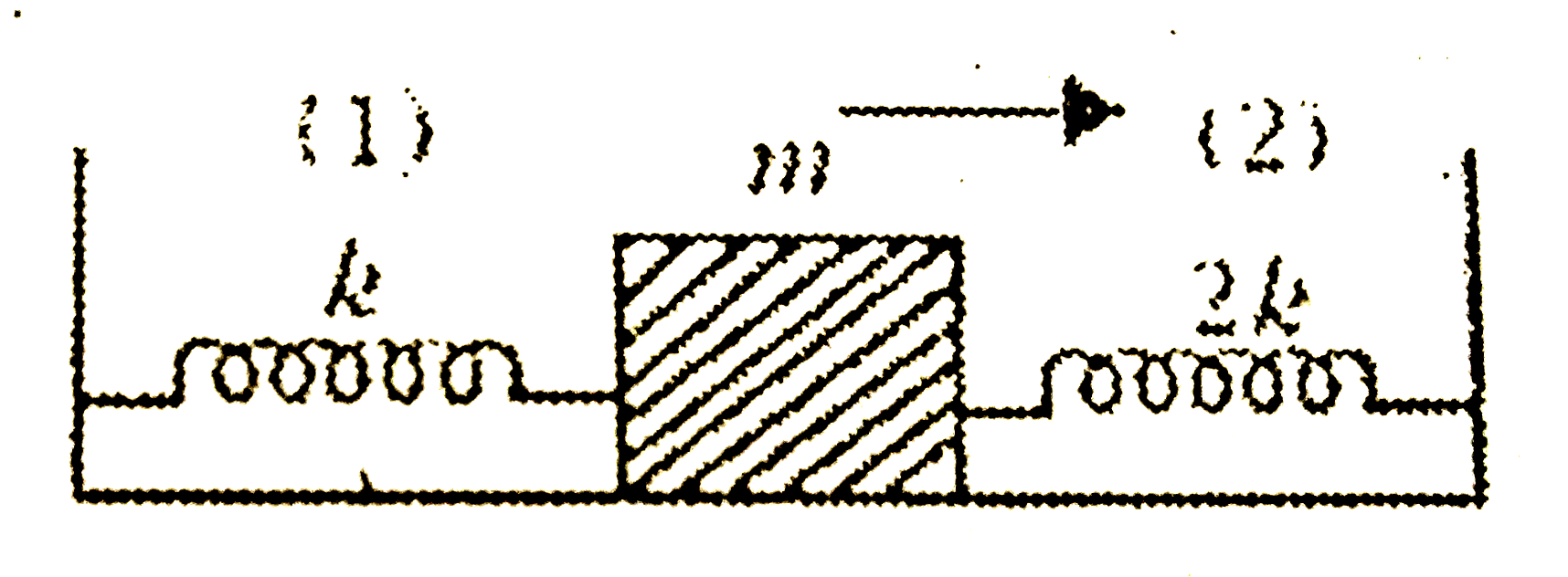
Let the mass m be displaced towards right by a distance x. Then the spring 1 will be extended and the spring 2 will be compressed by an amount of x each. The restoring force on mass m due to spring 1 is F1=−kx
And the restoring force due to spring 2 is
F2=−(2k)x
∴ Total force on the mass m is
F=F1+F2=−kx−2kx=−3kx
⇒md2xdt2=−3kx⇒d2xdt2+3kmx=0
⇒d2xdt2+ω2x=0 where ω2=3km⇒ω=√(3km)
⇒=ω2π=12π√3km
Topper's Solved these Questions
Similar Questions
Two springs of force constants K1 and K2 are connected to a mass m as shown I the figure.

If both K1 and K2 are made four times their original values, the frequency of oscillation becomes,
View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View Solution
Knowledge Check
Two springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mkTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mkTwo springs of force constants k1 and k2, are connected to a mass m as shown. The frequency of oscillation of the mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
_E01_383_Q01.png) Af/2Bf/4C4fD2f
Af/2Bf/4C4fD2f
Two springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are k1andk2, shown that frequency of oscillation of mass m is

View SolutionA block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-

View SolutionTwo springs, of force constants k1 and k2, are connected to a mass maas shown. The frequency of oscillation of mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes

View SolutionIn the figure all spring are identical having spring constant k and mass m each .The block hav also mass m .The frequency of oscillation of the block is
View SolutionTwo springs are joined and connected to mass m as shown. If the springs separately have force constants K1 and K2 , then frequency of oscillation of mass m is

View Solution

