A radioactive substance has a half-life of 64.8 h. A sample containing this isotope has an initial activity $(t = 0)$ of $40 μ C i$ . Calculate the number of nuclei that decay in the time interval between $t_{1} = 10.0 h$ and $t_{2} = 12.0 h$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C, D

$R_{0} = λ N_{0} \Rightarrow N_{0} = \frac{R_{0}}{λ}$
where, $λ = \frac{I n 2}{t_{1 / 2}}$
$N = N_{0^{e - λ t}}^{e - λ t}$
Find $N_{1} = N_{0 e^{- λ t 1}}^{- λ t 1}$
and $N_{2} = N_{0 e^{- λ t 2}}^{- λ t 2}$
$∴$ Number of nuclei decayed in given
time $= N_{1} - N_{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS DUAL NATURE OF RADIATION AND MATTER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Half-life period of a radioactive substance is $6 h$ . After $24 h$ activity is $0.01 μ C$ , what was the initial activity ?
A $0.04 μ C$
B $0.08 μ C$
C $0.24 μ C$
D $0.16 μ C$
Question 2 - Select One
A radioactive sample undergoes decay as per the following gragp. At time $t = 0$ , the number of undecayed nuclei is $N_{0}$ . Calculate the number of nuclei left after $1 h$ .
.
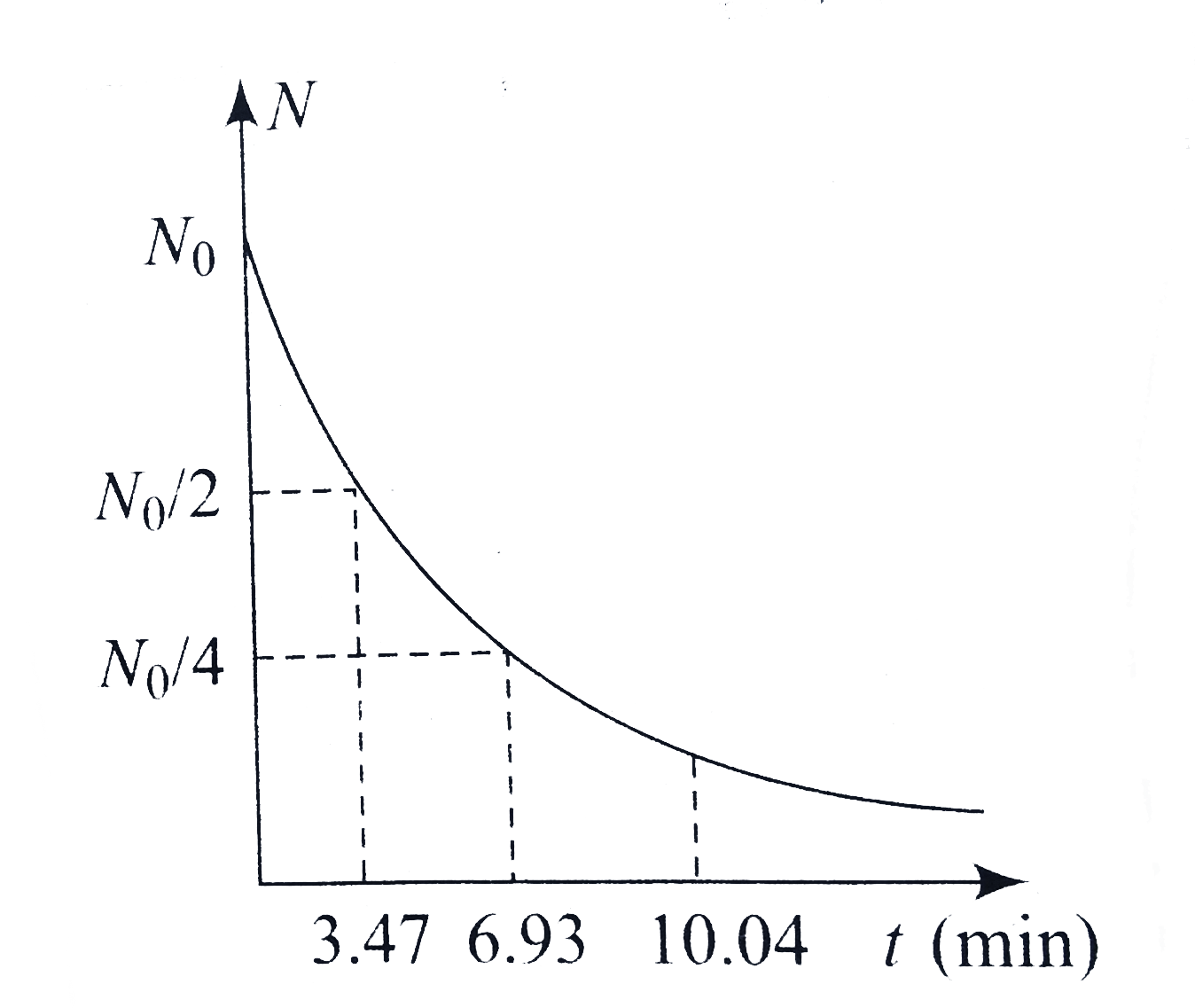A $N_{0} / e^{8}$
B $N_{0} / e^{10}$
C $N_{0} / e^{12}$
D $N_{0} / e^{14}$
Question 3 - Select One or More
Two radioactive substances have half-lives T and 2T. Initially, they have equal number of nuclei. After time $t = 4 T$ , the ratio of their number of nuclei is x and the ratio of their activity is y. Then,
A(a) $x = 1 / 8$
B(b) $x = 1 / 4$
C(c) $y = 1 / 2$
D(d) $y = 1 / 4$

DC PANDEY-MODERN PHYSICS - 2-Exercise 34.1

Home
Ask Doubt
Profile