The energy levels of a hypothetical one electron atom are given by En=−18.0n2eV
where n = 1,2,3,…. (a) Compute the four lowest energy levels and construct the energy levels diagram. (b) What is the first excitation potential (c ) What wavelength (Å) can be emitted when these atoms in the ground state are bombarged by electrons that have been accelerated through a potential difference of 16.2 V? (e) what is the photoelectric threshold wavelength of this atom?
The correct Answer is:A, C, D
(a) E1=−18.0((1))2=18.0eV
E2=18.0((2))2=−4.5eV
E3=−18.0((3))2=−2.0eV
E4=−18.0((4))2=−1.125eV
The energy level diagram is shown in figure
______E4=−1.125eV
______E3=−2.0eV
______E2=−4.5eV
_____E_1=−18.−0eV
(b) E2=13.5eV
∴Firstexcitationpotentialis13.5V<br>(c)E≠rgyofthee≤ctronae≤ratedbyapotentiald⇔erenceof16.2Vis16.2eV.Withthise≠rgythee≤ctroncanexcitethea→momn=1→n=3as.<br>E_4 - E_1 = -1.125 - (-18.0) = 16.875 eVgt 16.2 eV<br>andE_3 - E_1 = - 2.0 - (-18.0)=16.0 eV lt16.2 0 eVlt 16.2 eV<br>Now,lambda_32 = (12375)/(E_3 - E_2 = (12375)/(-2.0 - ((-4.5))<br>=4950 Å<br>λ31=12375E3−E2=1237516=773Å
and λ21=12375E2−E1=12375(−4.5−(−18.0)
=917Å
(d) No, the energy correspondingt to λ=2000Åis
E = (12375)/(2000) = 6.1875 eV<br>Theminiμmexcitatione≠rgyis13.5eV(n=1→n=2)<br>.(e)Thresholdwave≤n>hforpho→emission→takeplaceomsuchana→mislambda_(min) = (12375)/(18)<br>=687.5 Å
Topper's Solved these Questions
- MODERN PHYSICS - 1BOOK - DC PANDEYCHAPTER - MODERN PHYSICS - 1EXERCISE - Exercise 33.1
6 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEYCHAPTER - MODERN PHYSICS - 1EXERCISE - Exercise 33.2
12 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEYCHAPTER - MODERN PHYSICS - 1EXERCISE - Example Type 4
3 Videos
- MODERN PHYSICSBOOK - DC PANDEYCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEYCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
Similar Questions
The energy levels of a hypothetical one electron atom are given
En=−18.0n2eV, where n=1,2,3 …
a Cumpete the four lowest energy levels and construct the energy level diagram .
b What is the excitation potential of the state n=2?
c What wavelengths (Å) can be emitted when these atoms in the ground stste are bombarded by electron that have been accelerate through a potential difference of 16.2V
d If these atoms are in the ground state , can they absorb radiation having a wavelength of 2000Å ?
e what is the photoclectric threshold wavelength of this atom ?
View SolutionWhat is the wavelength of light emitted when the electron of a hydrogen atom undergoes a transition from an energy level with n=4 to an energy level with n=2? .What is the colour corresponding to this wavelength ?
View Solution
Knowledge Check
The energy levels of a hypothetical one - electron atom system are given by En=16n2eV, where n=1,2,3,……. . The wavelength of emitted photom corresponding to the transitition from first excited level to ground level is about
A1035 ÅB1220 ÅC3650 ÅD690 ÅThe energy levels of a hypotherical one electron atom are shown in figure
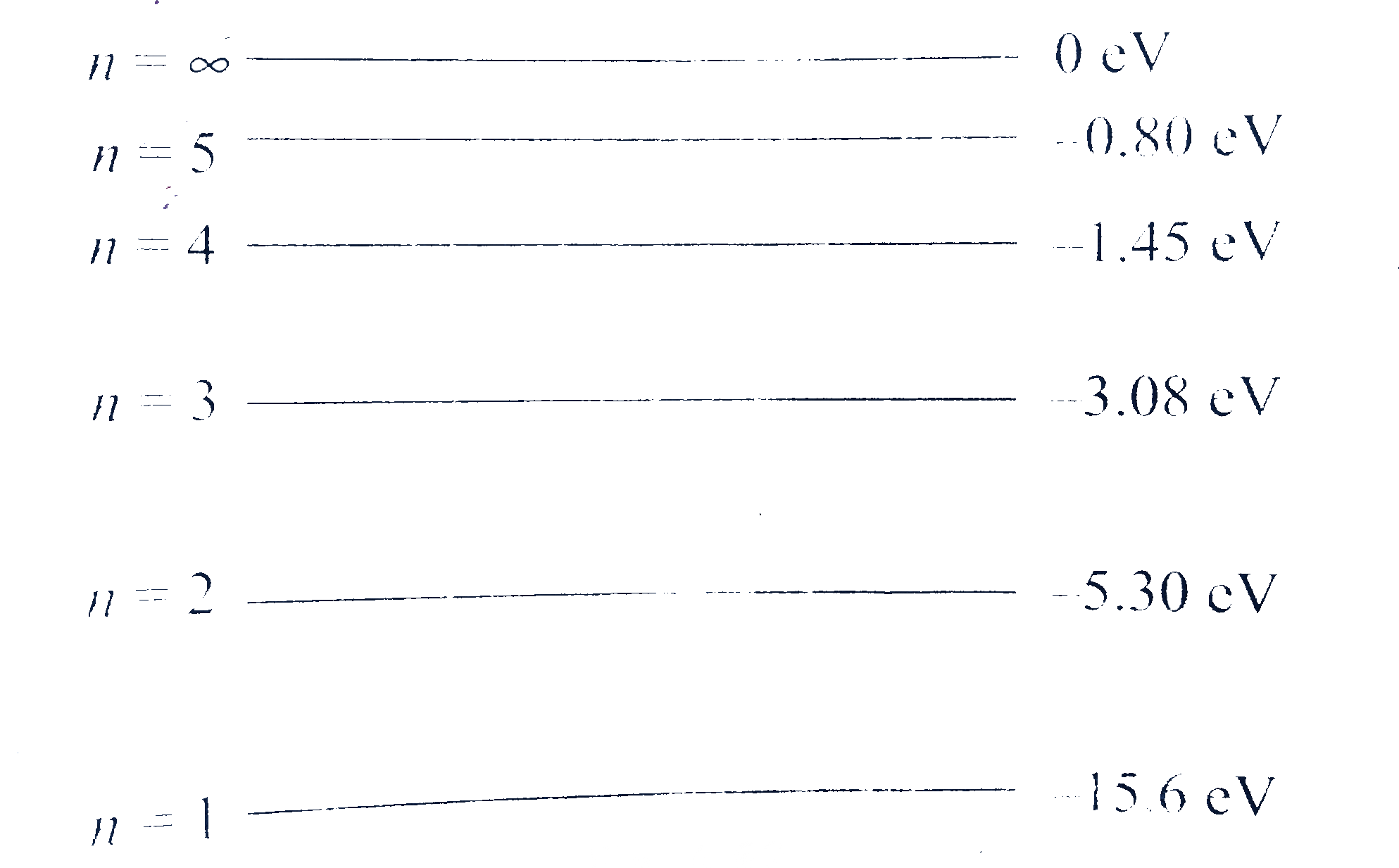
Find the excitation potential for the state n=3.A14.64eVB9.93eVC12.52eVD10.04eVThe energy levels of a hypotherical one electron atom are shown in figure

Find the short wavelength limit of the series terminating at n=2.A3256ÅB2339ÅC2509ÅD3494Å
An electron is in the ground state of a hydrogen atom. A photon is absorbed by the atom and the electron is excited to the n= 2 state. What is the energy in eV of the photon?
View SolutionCalculate wavelength of photon emitted when an electron goes from n=3 to n=2 level of hydrogen atom.
View SolutionAn electron is excited to fourth energy level in an atom. It will
View SolutionTwo energy levels of an electron in an atom are separated by 2.3 eV. The frequency of radiation emitted when the electrons go from higher to lower level is
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
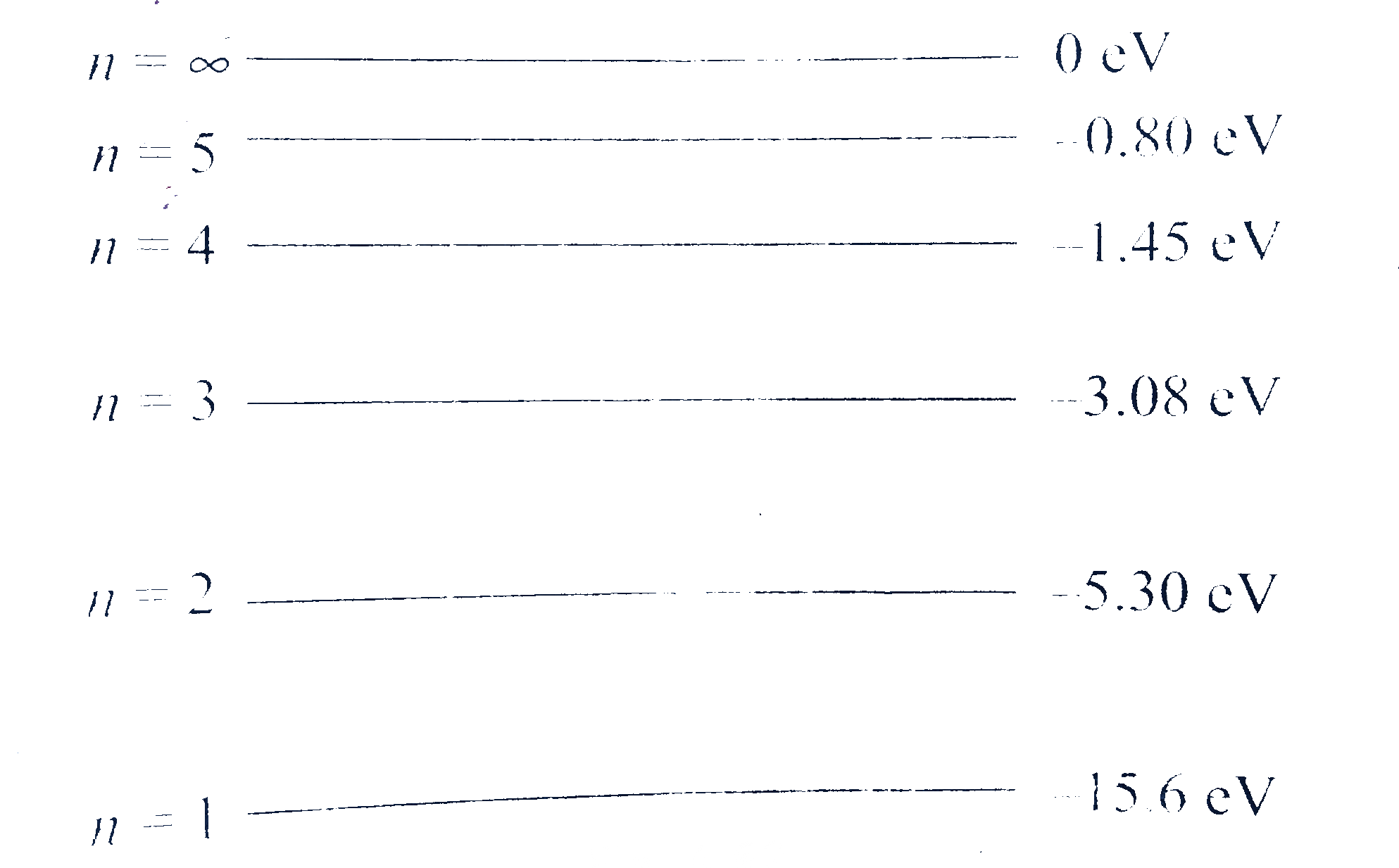
If an electron with initial kinetic energy 6eV is to interact with this hypothetical atom , what minimum energy will this electron carry after interaction?
View Solution
