An interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
To find the x-coordinates on the x-axis where maximum intensity is observed due to the interference of two coherent sources S1 (at the origin) and S2 (at (0,3λ,0)), we will follow these steps:
Step 1: Understand the setup
- The sources S1 and S2 are coherent and separated by a distance of 3λ.
- A detector D is moved along the positive x-axis.
Step 2: Determine the path difference
The path difference Δx between the waves arriving at the detector from S1 and S2 is given by:
Δx=S2D−S1D
Where S1D is the distance from S1 to the detector at point D(x,0) and S2D is the distance from S2 to the detector.
Step 3: Calculate distances
- The distance from S1 to D is:
S1D=√x2+02=x
- The distance from S2 to D is:
S2D=√x2+(3λ)2=√x2+9λ2
Step 4: Set up the path difference equation
The path difference is:
Δx=S2D−S1D=√x2+9λ2−x
Step 5: Condition for maximum intensity
For constructive interference (maximum intensity), the path difference must be an integer multiple of the wavelength:
Δx=nλ(n=0,1,2,…)
Thus, we have:
√x2+9λ2−x=nλ
Step 6: Rearranging the equation
Rearranging gives:
√x2+9λ2=nλ+x
Now, squaring both sides:
x2+9λ2=(nλ+x)2
Expanding the right side:
x2+9λ2=n2λ2+2nλx+x2
Cancelling x2 from both sides:
9λ2=n2λ2+2nλx
Step 7: Solve for x
Rearranging gives:
9λ2−n2λ2=2nλx
Factoring out λ2:
λ2(9−n2)=2nλx
Thus:
x=(9−n2)λ2n
Step 8: Determine valid values of n
To find valid values of n:
- 9−n2>0 implies n2<9, hence n=1,2,3.
Step 9: Calculate x for each n
1. For n=1:
x=(9−12)λ2⋅1=8λ2=4λ
2. For n=2:
x=(9−22)λ2⋅2=5λ4
3. For n=3:
x=(9−32)λ2⋅3=0(excluded)
Final Result
The x-coordinates on the x-axis where maximum intensity is observed (excluding x=0 and x=∞) are:
- x=4λ
- x=5λ4
- The sources S1 and S2 are coherent and separated by a distance of 3λ.
- A detector D is moved along the positive x-axis.
The path difference Δx between the waves arriving at the detector from S1 and S2 is given by:
Δx=S2D−S1D
Where S1D is the distance from S1 to the detector at point D(x,0) and S2D is the distance from S2 to the detector.
- The distance from S1 to D is:
S1D=√x2+02=x
- The distance from S2 to D is:
S2D=√x2+(3λ)2=√x2+9λ2
The path difference is:
Δx=S2D−S1D=√x2+9λ2−x
For constructive interference (maximum intensity), the path difference must be an integer multiple of the wavelength:
Δx=nλ(n=0,1,2,…)
Thus, we have:
√x2+9λ2−x=nλ
Rearranging gives:
√x2+9λ2=nλ+x
Now, squaring both sides:
x2+9λ2=(nλ+x)2
Expanding the right side:
x2+9λ2=n2λ2+2nλx+x2
Cancelling x2 from both sides:
9λ2=n2λ2+2nλx
Rearranging gives:
9λ2−n2λ2=2nλx
Factoring out λ2:
λ2(9−n2)=2nλx
Thus:
x=(9−n2)λ2n
To find valid values of n:
- 9−n2>0 implies n2<9, hence n=1,2,3.
1. For n=1:
x=(9−12)λ2⋅1=8λ2=4λ
2. For n=2:
x=(9−22)λ2⋅2=5λ4
3. For n=3:
x=(9−32)λ2⋅3=0(excluded)
The x-coordinates on the x-axis where maximum intensity is observed (excluding x=0 and x=∞) are:
- x=4λ
- x=5λ4
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEYChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Exercise 32.1
Explore 3 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEYChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Exercise 32.2
Explore 6 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEYChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Example Type 6
Explore 3 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:All Questions
Explore 120 Videos
- MAGNETIC FIELD AND FORCESBook:DC PANDEYChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
Similar Questions
An inteference is observed due to two coherent sources A and B separated by a distance 4λ along Y-axis, where λ is the wavelength of light. A detector 'D' is moved alog the positive X-axis. Find the totla number of maxima observe on the X-axis excluding the points x=0 and x=∞ ?

View SolutionAn inteference is observed due to two coherent sources A and B separated by a distance 4λ along Y-axis, where λ is the wavelength of light. A detector 'D' is moved alog the positive X-axis. Find the total number of maxima observe on the X-axis excluding the points x=0 and x=∞ ?

View Solution
Knowledge Check
An interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0, 3l, 0). Here, λ is the wavelength of the sources. Both sources are having equal intensity I0. A detector D is moved along the positive x-axix.

Find x-coordinates on the x-axis (exchange x=0 and x=OO).Ax=4λBx=7λ/4Cx=5λ/4Dx=3λAn interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0, 3l, 0). Here, λ is the wavelength of the sources. Both sources are having equal intensity I0. A detector D is moved along the positive x-axix.

Total number of black points observed by the observer on positive x-axis isAtwoBfourCthreeDfiveAn interference is observed due to two coherent sources separated by a distance 5λ along Y-axis, where λ is the wavelength of light A detector D is moved along the positive X -axis The number of point on the X-axis excluding the points x=0 and x=∞ at which resultant intensity will be maximum are
A4B5C∞Dzero
Two coherent sources Sf and S2 (in phase with ech other) are placed at a distance of 2λ as shown where λ is wavelength of sound. A detector moves on line AB parrallel to S1S2. If detector detects maximum intensity at finite distance from O at θ=±(πn). Find n

View SolutionThere are two coherent sources S1 and S2 which produce waves in same phase placed on Y axis at points (0, 2d) and (0, d) as shown in figure-6.23. A detector D is placed at origin which moves along X direction, find the number of maxima recorded by detector excluding points x = 0 and x=∞. Given that wavelength of light produced is 6200Å and separation between sources is 0.34 mm.

View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionTwo coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
View SolutionTwo coherent sources emit light of wavelength λ. Separation between them, d=4λ.
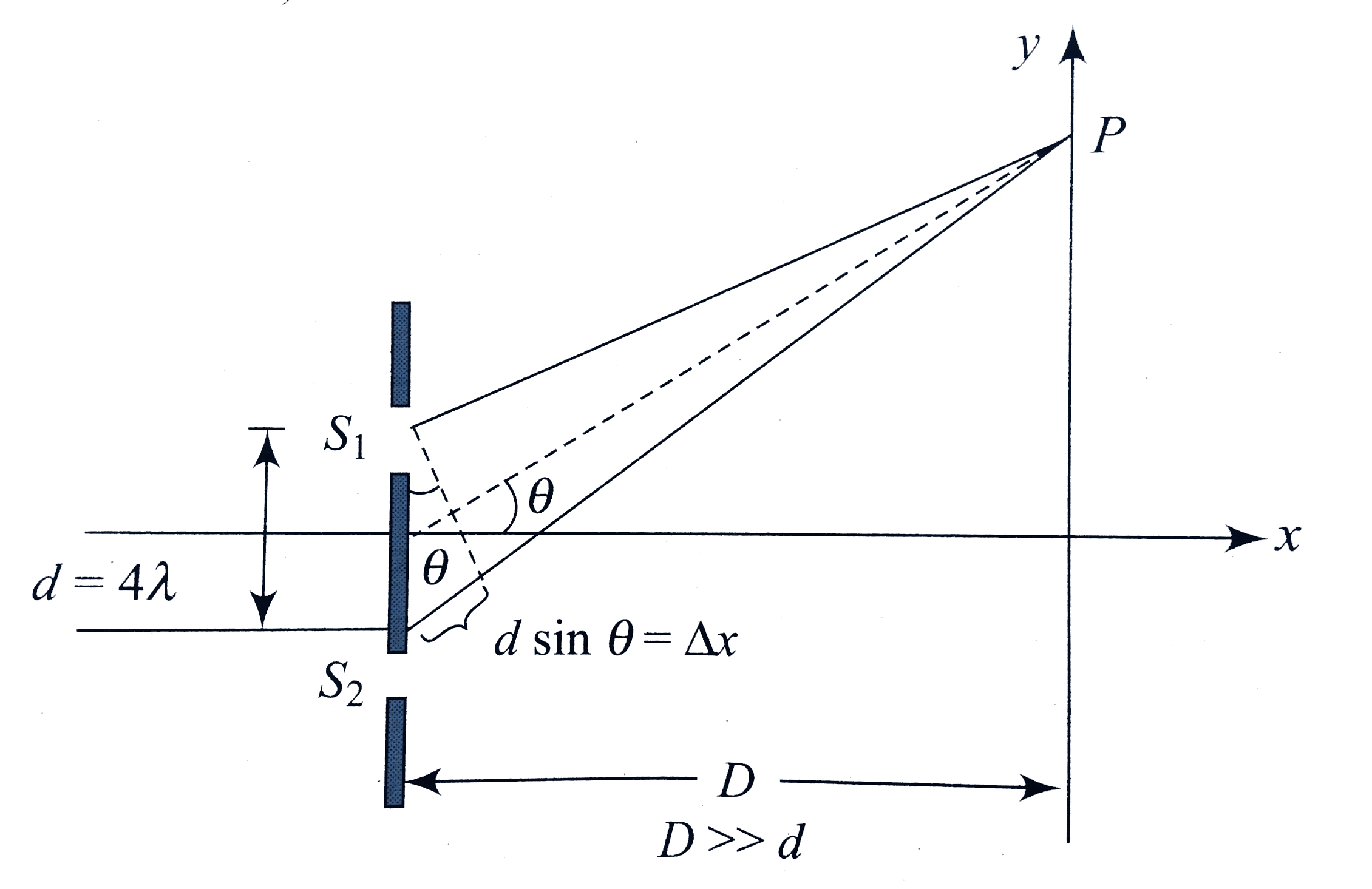
If a detector moves along the y-axis, what is the maximum number of minima observed?
If the detector moves along 'x-axis beginning from S2, the maximum number of minima observed is
View Solution
