Given that .1μ2=4/3,.2μ3=3/2. Find .1_μ3.
The correct Answer is:B
.1μ2×.2μ3×.3μ1=1
∴43×32=1.3μ1=.1μ3 or .1μ3
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:DC PANDEYChapter:REFRACTION OF LIGHTExercise:Exercise 31.2
Explore 2 Videos
- REFRACTION OF LIGHTBook:DC PANDEYChapter:REFRACTION OF LIGHTExercise:Introductory exercise
Explore 4 Videos
- REFRACTION OF LIGHTBook:DC PANDEYChapter:REFRACTION OF LIGHTExercise:Solved Example
Explore 15 Videos
- REFLECTION OF LIGHTBook:DC PANDEYChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
- SEMICONDUCTORSBook:DC PANDEYChapter:SEMICONDUCTORSExercise:Subjective
Explore 12 Videos
Similar Questions
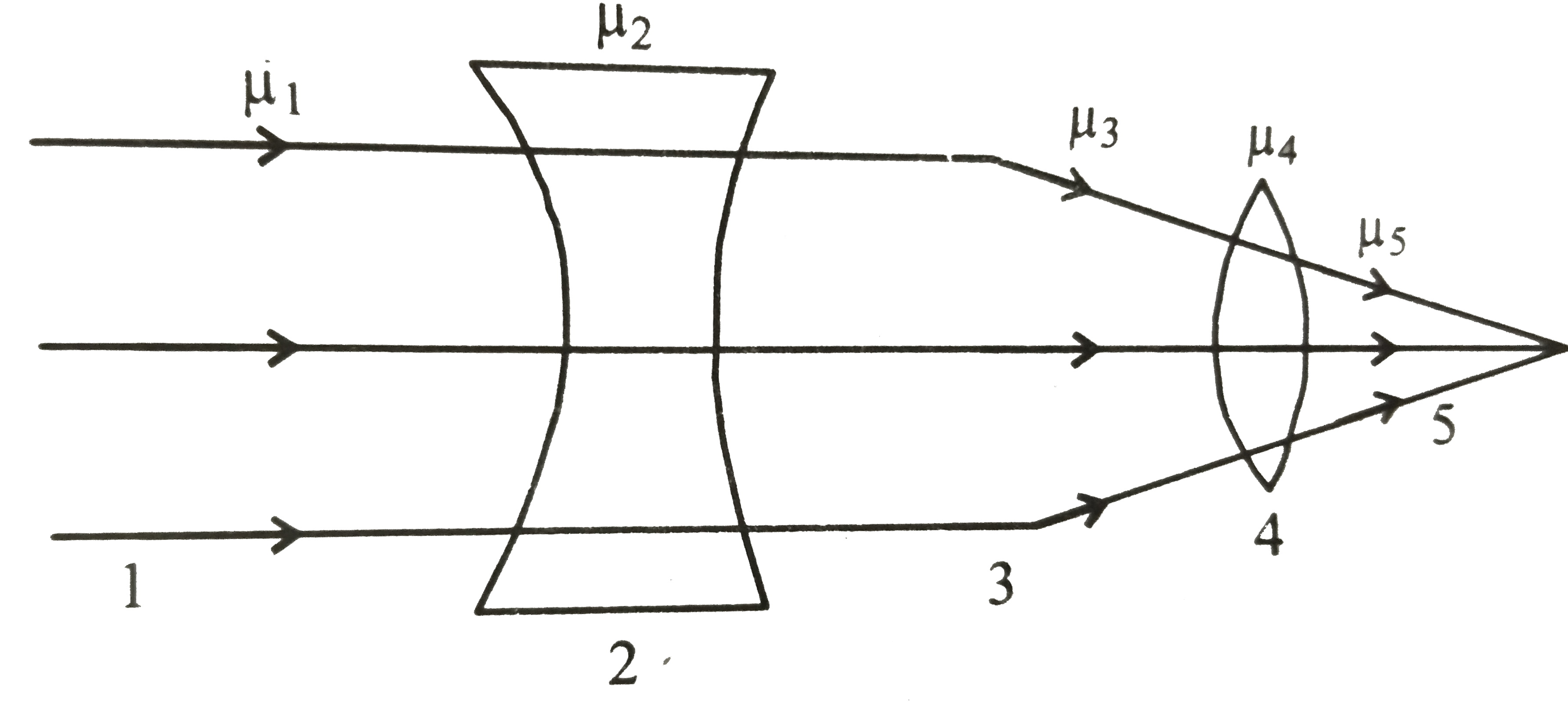
In the figure shown μ1,μ2,μ3,μ4andμ5 are the refractive
indices of the mediums 1,2,3,4 and 5 respectively. Consider
the following:
(1) μ1=μ2 (2) μ3=μ4=μ5
(3) μ2<μ3 (4) μ4>μ5
Which of the above are correct?
View SolutionFocal length of a convex lense in air is 10cm. Find its focal
length in water. Given that μg=3/2 and μw=4/3.
View Solution
Knowledge Check
If .iμj represents refractive index when a light ray goes from mefium i to medium j, then the product .2μ1×.3μ2×.4μ3 is equal to
A.3μ1B.3μ2C1.1μ4D.4μ2The ratio of angle of minimum deviation of a prism in air and when dipped in water will be (.aμg=3/2and.aμw=4/3)
A1/8B1/2C3/4D1/4If xμy represents the refractive index when a ray of light goes from medium x to medium y , then the product 2μ1×3μ2×4μ3 is equal to
A2μ1B11μ4C3μ2D4μ2
The deviation produced by a thin glass prism placed in air, when immersed in water is
[Given aμg=3/2andaμw=4/3]
View SolutionA double convex lens, lens made of a material of refractive index μ1, is placed inside two liquids or refractive indices μ2 and μ3, as shown. μ2>μ1>μ3. A wide, parallel beam of light is incident on the lens from the left. The lens will give rise to

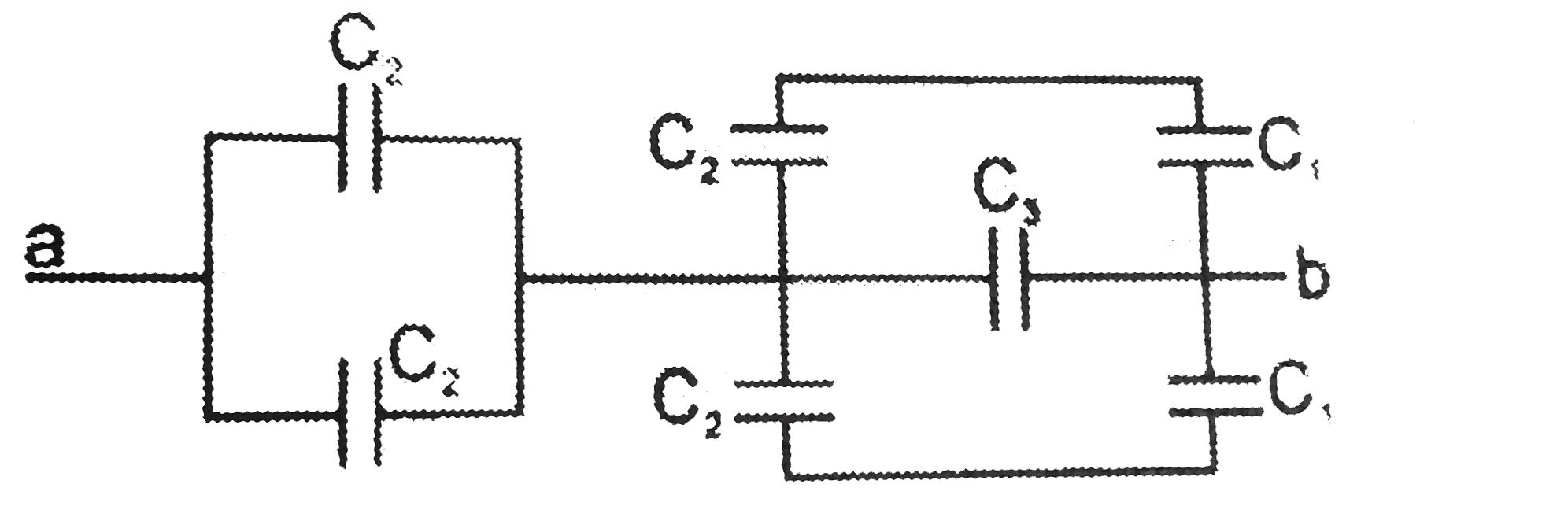
View SolutionA combination arrangement of the capacitors is shown in the figure
(i) C1=3μF,C2=6μF and C3=2μF then equivalent capacitance between 'a' and 'b' is :
View SolutionIn the figure shown μ1,μ2,μ3,μ4andμ5 are the refractive indices
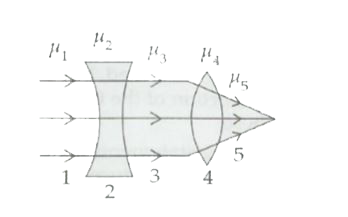
of the mediums 1,2,3,4 and 5 respectively . Consider the following
(1) μ1=μ2 (2) μ3=μ4=μ5
μ2<μ3 (4) μ4>μ5
View SolutionThere are three optical media 1,2 and 3 with their refractive index μ1, μ2 and μ3 such that μ1>μ2>μ3 choose the correct options (TIR means total internal reflection)
View Solution