A boy of height 1.5m with his eye level at 1.4m stands before a plane mirror of length 0.75 m fixed on the wall. The height of the lower edge of the mirror above the floor is 0.8 m. Then ,
the boy will see his full image
the boy cannot see his hair
the boy cannot see his feet
the boy can see neither his hair nor his feet.
The correct Answer is:C
To solve the problem, we need to analyze the situation involving the boy, his eye level, and the plane mirror.
1. Identify the Height of the Boy and Eye Level:
- The height of the boy is given as 1.5 meters.
- The eye level of the boy is at 1.4 meters.
2. Determine the Position of the Mirror:
- The lower edge of the mirror is positioned at a height of 0.8 meters above the floor.
- The length of the mirror is 0.75 meters.
3. Visualize the Setup:
- Draw a vertical line representing the wall with the mirror.
- Mark the height of the boy (1.5 m) and his eye level (1.4 m).
- Indicate the position of the mirror starting from 0.8 m to 1.55 m (0.8 m + 0.75 m).
4. Calculate the Distance from Eye Level to the Bottom of the Mirror:
- The distance from the boy's eye level (1.4 m) to the bottom of the mirror (0.8 m) is:
1.4m−0.8m=0.6m
5. Determine the Reflection Point:
- The ray of light from the boy’s eyes will reflect off the mirror. The highest point of the mirror is at 1.55 m (0.8 m + 0.75 m).
- The ray will reflect downwards from the top edge of the mirror.
6. Calculate the Maximum Height Visible in the Mirror:
- Since the boy's eye level is at 1.4 m, and the mirror reflects light downwards, the highest point he can see in the mirror is at the height of the mirror (1.55 m).
- The distance from the boy's eye level to the top of the mirror is:
1.55m−1.4m=0.15m
7. Determine the Part of the Boy Not Visible:
- The boy's total height is 1.5 m, and he can see up to 1.55 m in the mirror. However, since the ray reflects from the top edge, the lowest point he can see is determined by the reflection.
- The distance from the bottom of the mirror (0.8 m) to the boy's feet (0 m) is:
0.8m−0m=0.8m
- Since the boy's eye level is at 1.4 m, he cannot see the part of his body below the line of sight to the mirror.
8. Conclusion:
- The boy cannot see his feet because the reflection only allows him to see up to 0.15 m above his eye level, which does not reach down to his feet.
Final Answer:
The boy cannot see his feet in the mirror.
- The height of the boy is given as 1.5 meters.
- The eye level of the boy is at 1.4 meters.
- The lower edge of the mirror is positioned at a height of 0.8 meters above the floor.
- The length of the mirror is 0.75 meters.
- Draw a vertical line representing the wall with the mirror.
- Mark the height of the boy (1.5 m) and his eye level (1.4 m).
- Indicate the position of the mirror starting from 0.8 m to 1.55 m (0.8 m + 0.75 m).
- The distance from the boy's eye level (1.4 m) to the bottom of the mirror (0.8 m) is:
1.4m−0.8m=0.6m
- The ray of light from the boy’s eyes will reflect off the mirror. The highest point of the mirror is at 1.55 m (0.8 m + 0.75 m).
- The ray will reflect downwards from the top edge of the mirror.
- Since the boy's eye level is at 1.4 m, and the mirror reflects light downwards, the highest point he can see in the mirror is at the height of the mirror (1.55 m).
- The distance from the boy's eye level to the top of the mirror is:
1.55m−1.4m=0.15m
- The boy's total height is 1.5 m, and he can see up to 1.55 m in the mirror. However, since the ray reflects from the top edge, the lowest point he can see is determined by the reflection.
- The distance from the bottom of the mirror (0.8 m) to the boy's feet (0 m) is:
0.8m−0m=0.8m
- Since the boy's eye level is at 1.4 m, he cannot see the part of his body below the line of sight to the mirror.
- The boy cannot see his feet because the reflection only allows him to see up to 0.15 m above his eye level, which does not reach down to his feet.
The boy cannot see his feet in the mirror.
Topper's Solved these Questions
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Exercise Level 1 Subjective
17 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Level 2 Single Correct
16 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Exercise Level 1 Assertion And Reason
10 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A boy 1.5m tall with his eye level at 1.38m stands before a mirror fixed on a wall. Indicate by means of a ray diagram how the mirror should be positioned so that he can view himself fully. What should be the minimum length of the mirror ? Does the answer depend on the eye level ?
View SolutionA person wants to see AB part of his image. His eye level is at 1.8m above the ground. If he uses minimum size of mirror required for this, find the height of the lowest point of mirror above the ground.
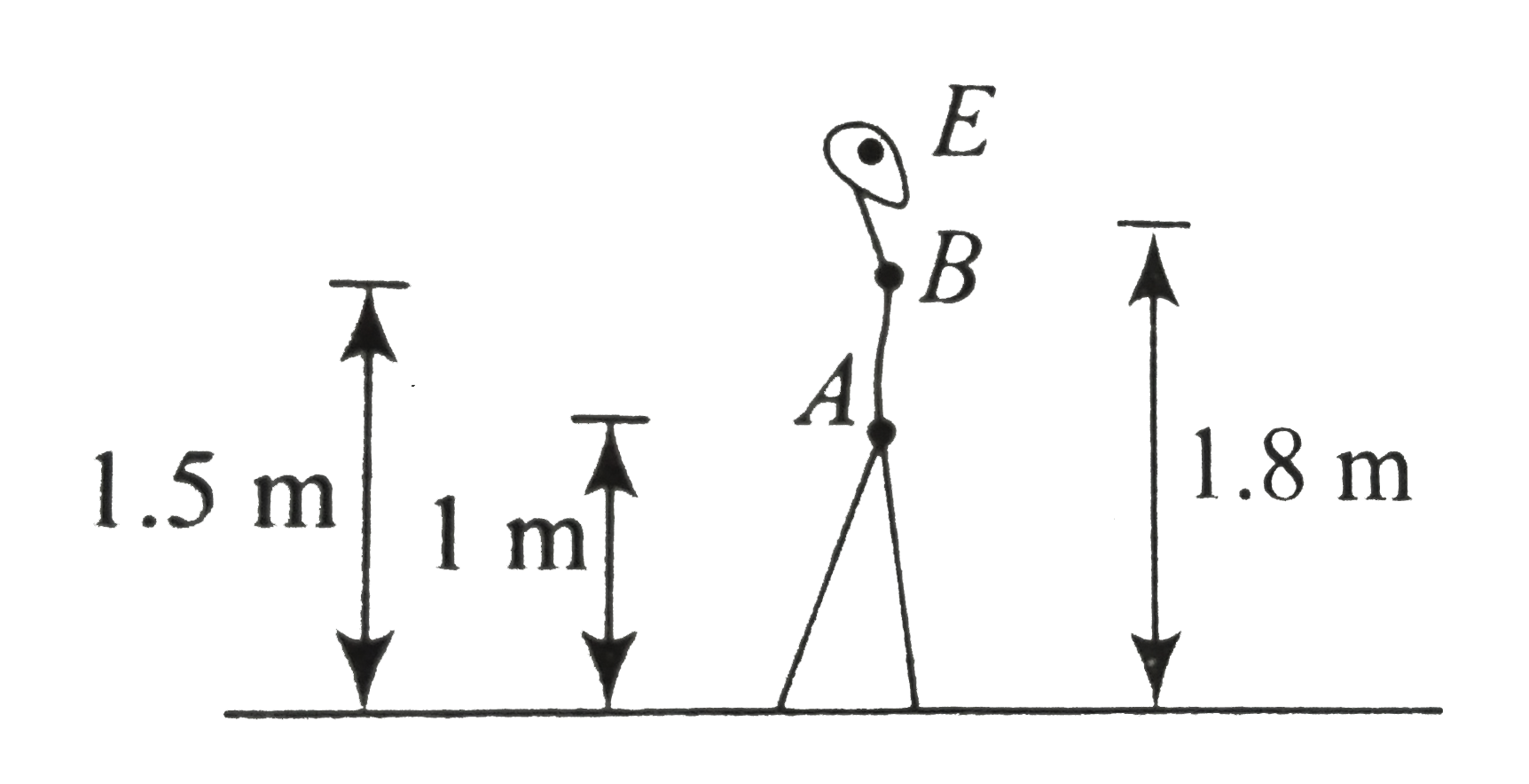
View Solution
Knowledge Check
A man of height 1.4 m wishes to see his full image in a plane mirror placed at distance of 2 m . the minimum height of the mirror should be
A0.5 mB0 . 7 mC0 . 9 mDnoneA boy of height 1m stands in front of a convex mirror. His distance from the mirror is equal to its focal length. The height of his image is
A0.25mB0.33mC0.5mD0.67mA man of height 1.6 m wishes to see his full image in a plane mirror placed at a distance of 2 m. The minimum length of the mirror should be
A0.4 mB0.8 mC1.6 mD2.4 m
A pole of height 4 m is kept in front of a vertical plane mirror
of length 2m. The lower end of the mirror is at a height of 6m form the grown
.the horizontal distance between the mirror and the pole is 2m. Up to what
minimum and maximum heights a man can see the image of top of the pole at a
horizontal distance of 4m (from the mirror O standing on the same horizontal
line which is passing through the pole and the horizontal point below the
mirror?

View SolutionA body of height 1m stands in front of a convex mirro. His distance from the mirror is equal to its focal length. The height of his image is
View SolutionA pole of height 1 . 8 m stands in front of a larger vertical plane mirror . The distance of the image from the pole at a distance of 1 . 5 m from the mirror is
View SolutionA person's eye is at a height of 1.5 m . He stands infront of a 0.3 m long plane mirror whose lower end is 0.8m above the ground. The length of the image he sees of himself is
View SolutionAn object of height 0.5 m is placed in front of convex mirror. Distance of object from the mirror is equal to the focal length of the mirror. Height of the image of the object is
View Solution
