A positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance r(r>R) from the center of the sphere. Find the minimum velocity v so that it can penetrate (R/2) distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.
The correct Answer is:A, B, C
From conservation of energy
Ui+Ki=Uf+Kf ltbr>gt orqVi+Ki=qVf+Kf
orq(Q4πε0r)+12mv2
=q(Q4πε0R3)(1.5r2−0.5R24)+0
12mv2=11Qq3πε0R−Qq4πε0r
or v=√Qq2πε0mR(r−Rr+38)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.14videos
ELECTROSTATICS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.29videos
ELECTROSTATICS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions120videos
GRAVITATION
Similar Questions
A charge q is uniformly distributed over the volume of a shpere of radius R. Assuming the permittively to be equal to unity throughout, find the potential
(a) at the centre of the sphere,
(b) inside the sphere as a function of the distance r from its centre.View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :
View Solution
Knowledge Check
- Question 1 - Select One
A conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
AVrBR2Vr3CRVr2DrVR2 - Question 2 - Select One
A conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
ARVr2BVRCrVR2DR2Vr2 - Question 3 - Select One
Metallic sphere of radius R is charged to potential V. Then charge q is proportional to
AVBRCbothDNone
A charge Q is uniformly distributed inside a non- conducting sphere of radius R. Find the electric potential energy stored in the system.
View SolutionA bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)
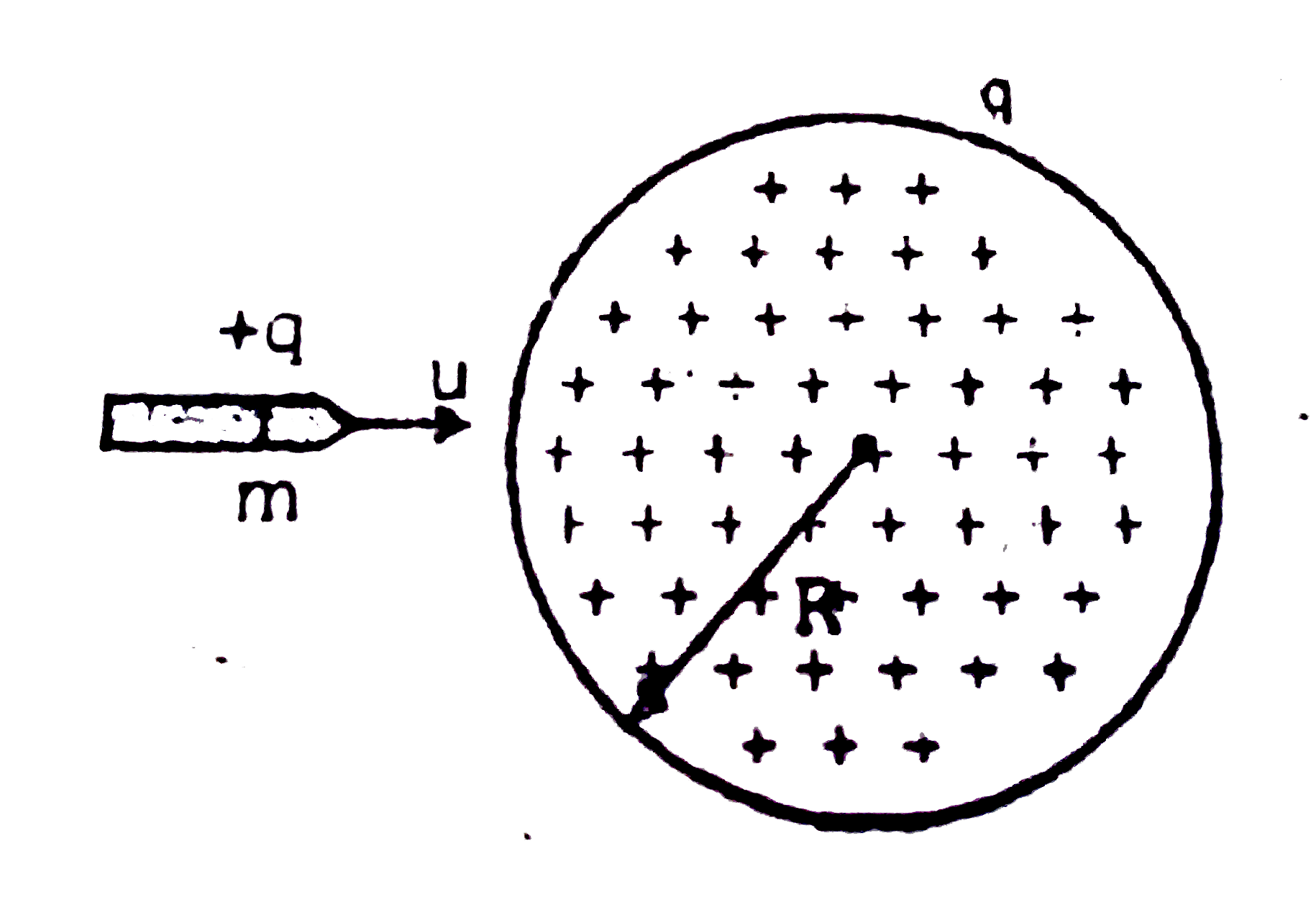
View SolutionA bullet of mass m and charge q is fired towards a solid unifromly charged sphere of redius R and total cbharge +q. If it strikes the surface of sphere with speed u, find the minimum speeed u so that it can penetrate through the sphere , (Neglect all resistance forces or friction acting on bullet except electrositatic forces )
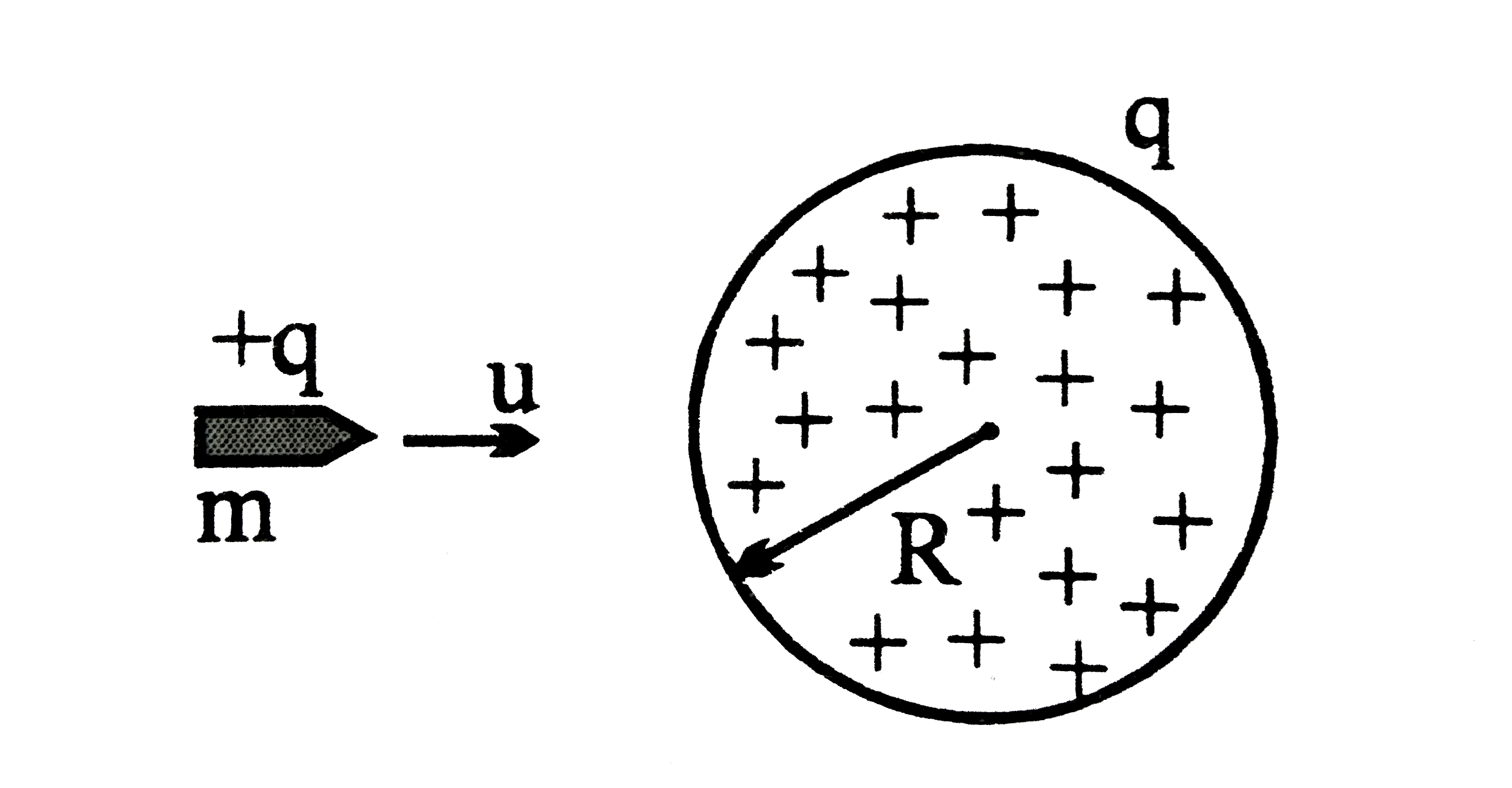.View SolutionThere is a cubical cavity inside a conducting sphere of radius R. A positive point charge Q is placed at the centre of the cube and another positive charge q is placed at a distance 1(>R) from the centre of the sphere. The sphere is earthed
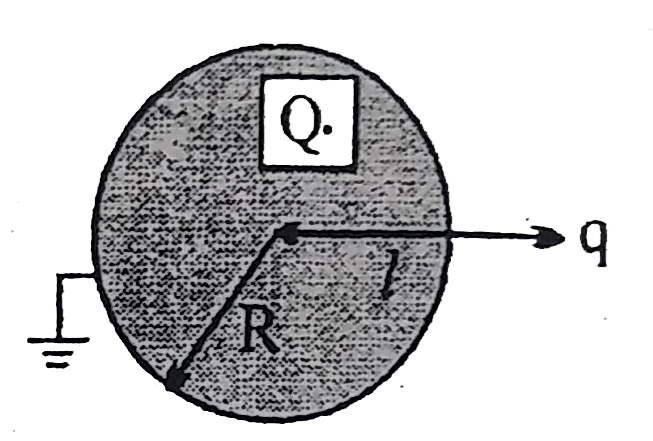
Net charge on the outer surface of conducting sphere isView SolutionThe electric intensity of outside a charged sphere of radius R at a distance r(r>R) is
View Solution