The electric field in a region is given by E=αxˆi. Here α is a constant of proper dimensions. Find
a. the total flux passing throug a cube bounded by the surface x=l,x=2l,y=0,y=l,z=0,z=l.
b. the charge contained inside in above cube.
The correct Answer is:A, B, C
a. Electric field is along positive x x-direction. Therfore,field lines are perpendicular to face ABCD and EFGH. At all other four faces field lines are tangential. So, net flux passing through these four facess will be zero. 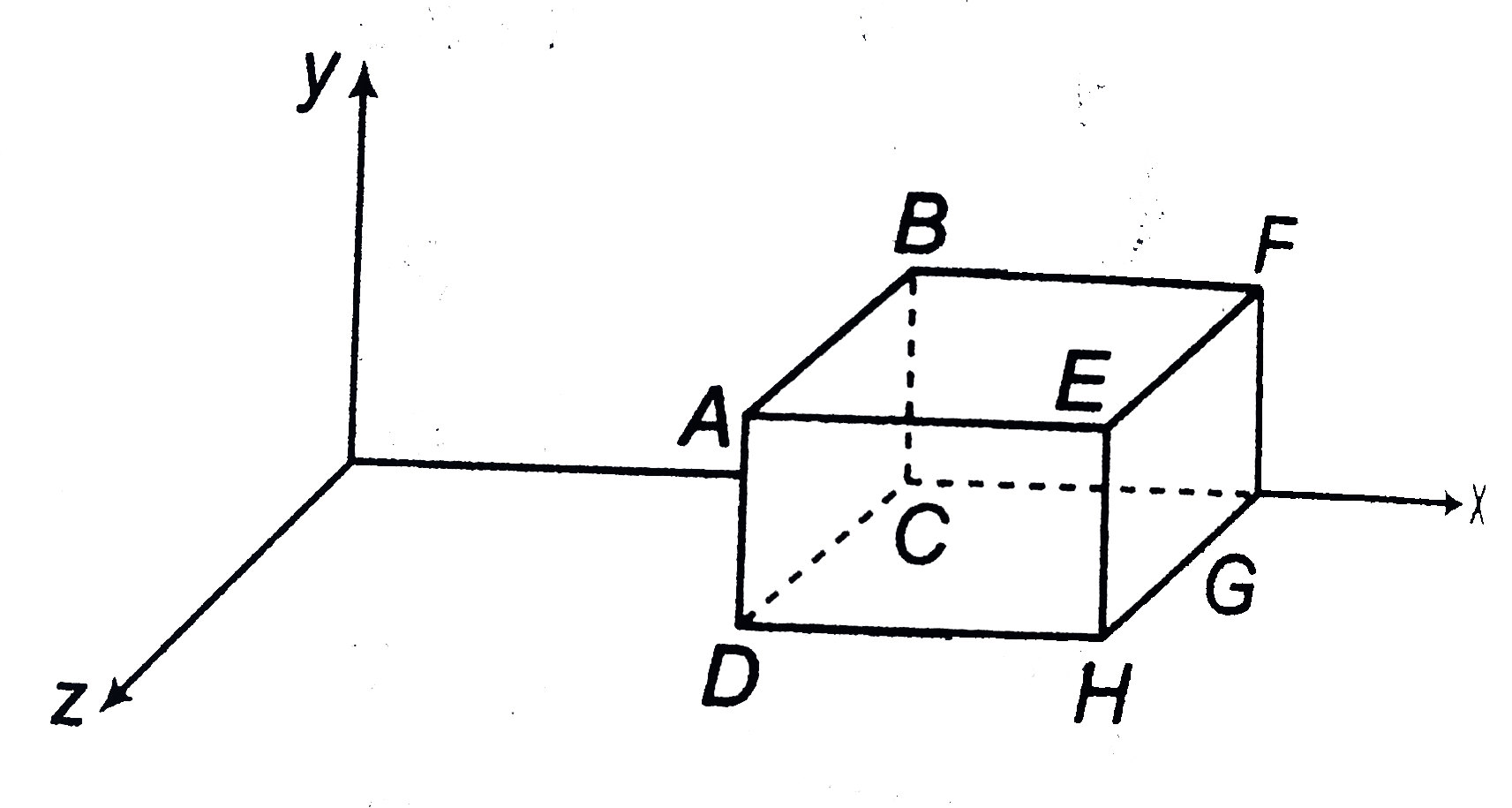
Flux entering at face ABCD at this face x=l 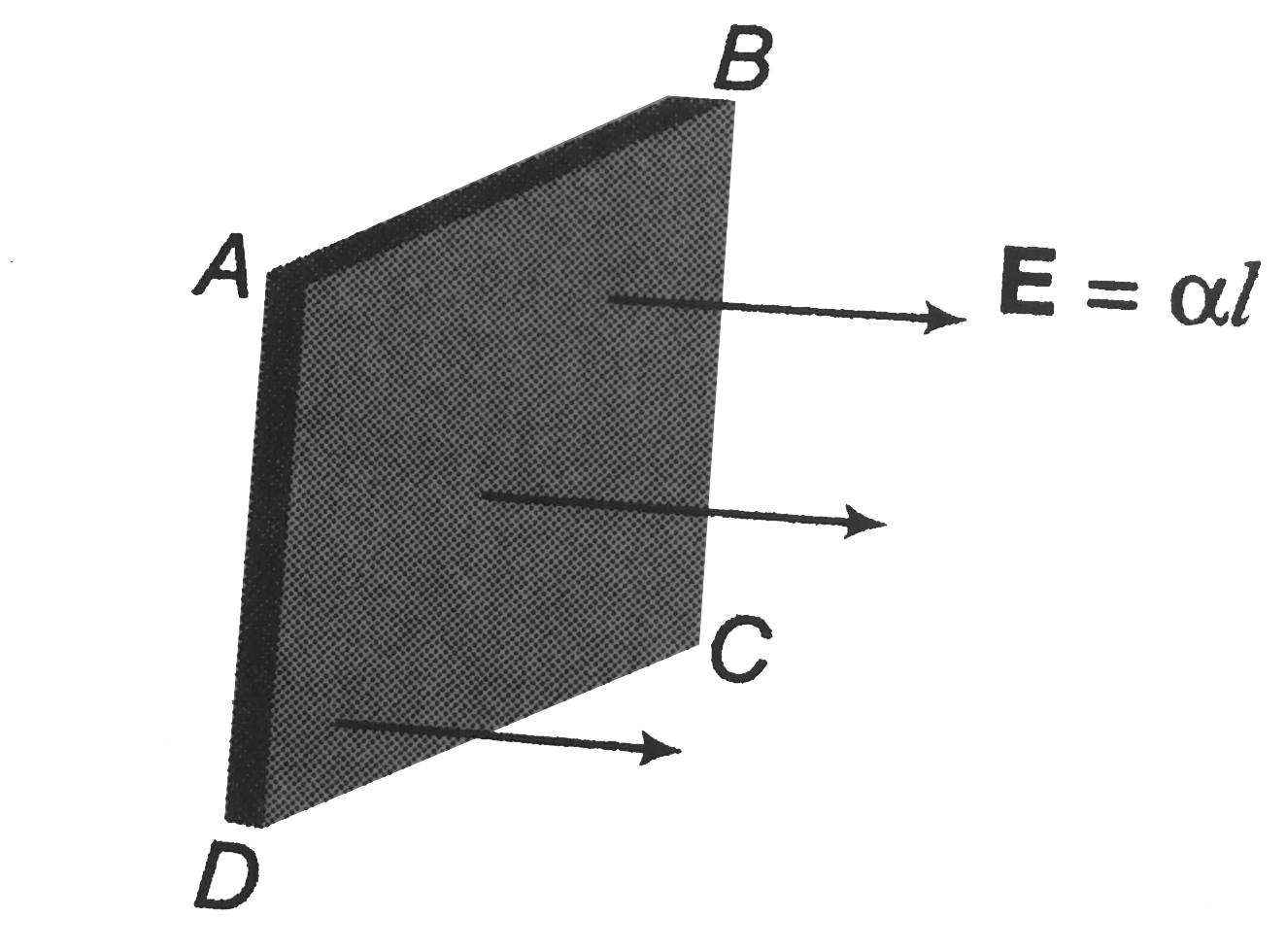
∴E=αlˆi
∴ Flux entering the cube from this face
ϕ1=ES=(αl)(l2)=αl3
Flux leaving the face EFGH At this face x=2l
∴E=2αlˆi
∴ Flux coming out of this face
ϕ2=ES=(2αl)(l2)
=2αl3
∴ Net flux passing through the cube,
ϕnet=ϕ2−ϕ1=2αl3−αl3
=αl3 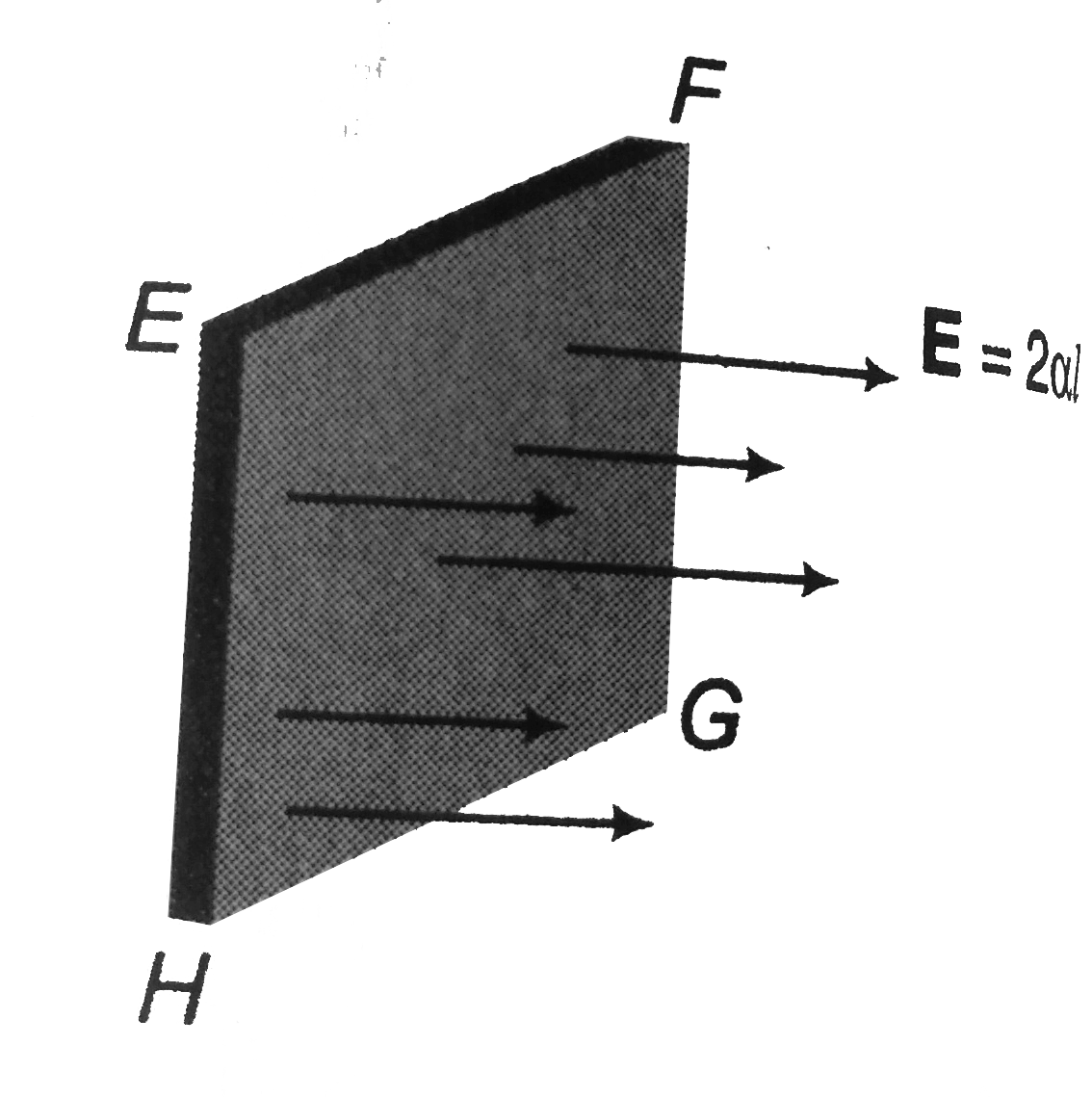
b. From Gauss's law,
ϕnet=qinε0
qin=(ϕnet(ε0)
=αεl3
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
The electric field in a region is given by →E=E0axˆi. Find the electric flux passing through a cubical volume bounded by the surfaces x=0,x=a,y=0,y=a,z=0 and z=a.
View SolutionThe electric field in a region is given by E=E0xlˆi. Find the charge contained inside a cubical 1 volume bounded by the surfaces x=0,x=a,y=0,yh=,z=0 and z=a. Take E0=5×103N/C l=2cm and a=1m.
View Solution
Knowledge Check
The electric field in a region is given by E=35E0ˆi+45E0j with E0=2.0x103N/C. Find the flux of this field through a rectangular surface of area 0.2m2 parallel to the y-z plane.
A24Nm2/CB240Nm2/CC440Nm2/CD44Nm2/CDue to a charge inside the cube, the electric field is: Ex = 600x, Ey = 0, Ez = 0. The charge inside the cube is nearly -
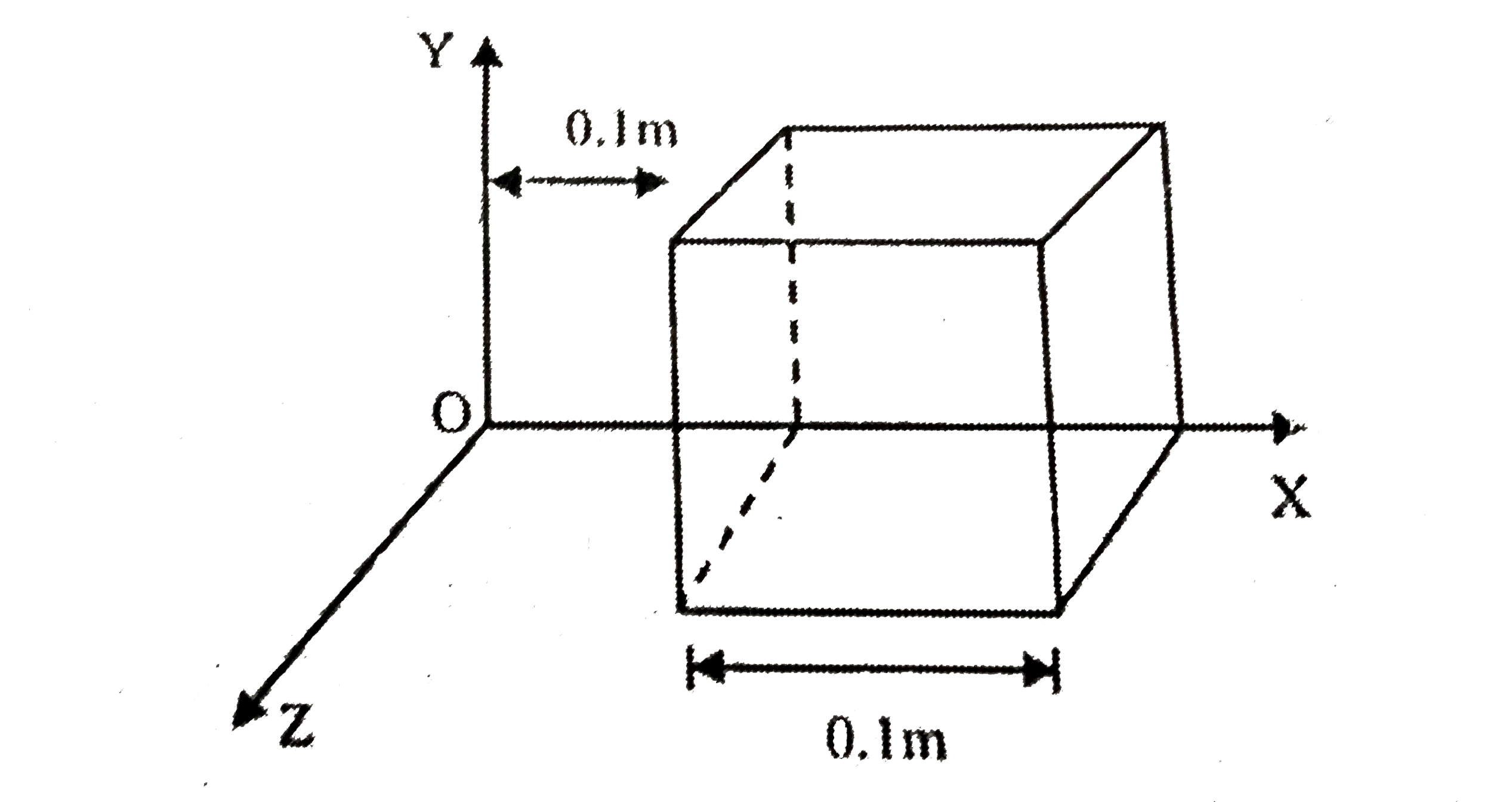 A600μCB60μCC53μCD6μC
A600μCB60μCC53μCD6μCAn infinite wire having charge density λ passes through one of the edges of a cube having length l. find the total flux passing through the cube
 Aλlε0Bλl4ε0Cλl6ε0DNone of these
Aλlε0Bλl4ε0Cλl6ε0DNone of these
The electric field in a region is given by →E=E0xˆi. The charge contained inside a cubical volume bounded by the surface x=0, x=2m, y=0, y=2m, z=0 and z=2m is nε0E0. Find the va,ue of n.
View SolutionThe electric field In a region is given gy →E=E0xbˆi. Find the charge contained in the cubical volume bounded by the surfaces x=0, x=a, y=0, y=a,z=0 and z=a. take E0=5×103NC−1,a=1cmandb=2cm.
View SolutionThe electric field in a region is given by →E=E0xι→i. Find the charge contained inside a cubical volume bounded by the curfaced x=0,x=α,y=0,y=α,z=0andz=α. Take E0=5×103NC−1, ι=2cmandα=1cm.
View SolutionThe electric fields in a region is given by →E=E0xLˆi ,Find the charge contained inside a cubical volume bounded by the surface x=0,x=L,y=0,y=L,z=0,z=L.
View SolutionFive electric dipoles having charges +q and -q are placed inside a cube having each side of length l. The total electric flux coming out of the cube is given by
View Solution
