Initially the spheres A and B are at potentials VA and VB. Find the potential of A when sphere B is earthed.
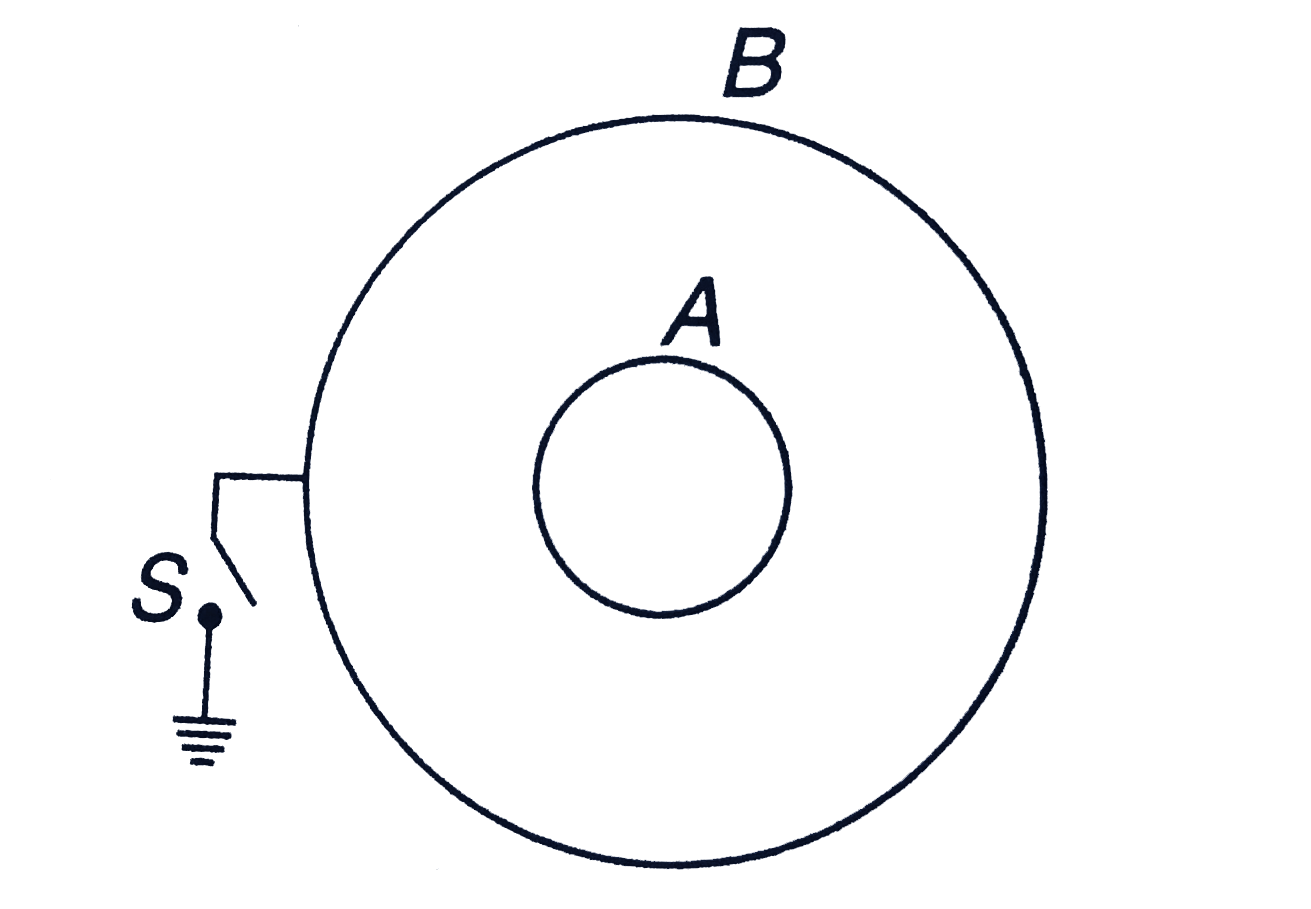
VA
0
VA+VB
VA−VB
The correct Answer is:D
As we have studied above that the potential difference between these two spheres depends n the charge on the inner sphere only. Hence, the PD will remain unchanged because by earthing the sphere B charge on A remains constant. Let V'A be the new potential at A. Then
VA−VB=V′A=V′B
but V′B=0 as it is earthed. Hence,
V′A=VA−VB
Topper's Solved these Questions
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Example Type 8
Explore 3 Videos
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Level 2 Single Correct
Explore 94 Videos
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Example Type 5
Explore 5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEYChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:All Questions
Explore 120 Videos
Similar Questions
A metal sphere A of radius a is charged to potential V. What will be its potential if it is enclosed ny a spherical conducting shell B of radius b and the two are connected by a wire ?
View SolutionA metal sphere A of radius 1m is charged to a potential of 20V .What will be its potential (in volt) when it is enclosed by a spherical conducting shell B of radius 2m and two are connected by a wire?
View Solution
Knowledge Check
A hollow metallic sphere of radius 0.1 m is charged to a potential of 5 V. The potential at its centre is
AinifiniteB5 VCzeroDcannot be determinedA charge is located at the center of sphere A (radius RA=0.0010 m), which is in the center of sphere B (radius RB=0.0012 m ). Spheres A and B are both equipotential surfaces. What is the ratio VA/VB of the potentials of these surfaces?
A0.42B1.2C0.83D1.4Consider three concentric metallic spheres A, B and C of radii a, b, c respectively where a<b<c, A and B are connected whereas C is grounded. The potential of the middle sphere B is raised to V then the charge on the sphere C is–
A−4πε0Vbcc−bB−4πε0Vacc−bC+4πε0Vbcc−bDZero
A metal sphere A of radius 1m is charged to a potential of 20V .What will be its potential (in volt) when it is enclosed by a spherical conducting shell B of radius 2m and two are connected by a wire?
View Solution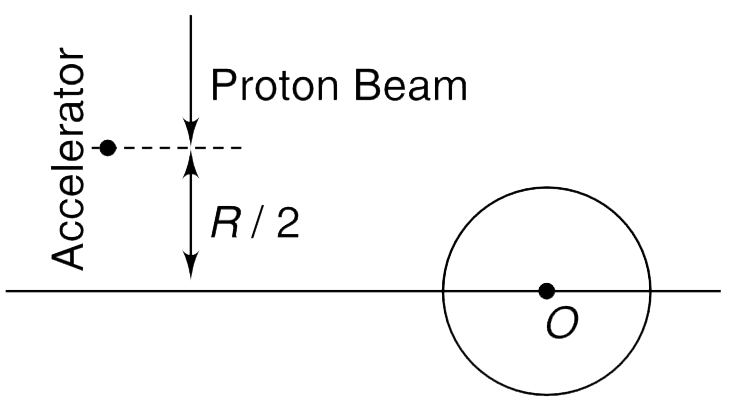
A proton accelerator produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharged distant metal sphere of radius R. The sphere is fixed and centered at point O. The initial path of the beam is at a distance of (R/2) from the centre, as indicated in the diagram. The protons in the beam that collide with the sphere get absorbed and cause it to become uniformly charged. The subsequent potential field at the accelerator due to the sphere can be neglected. Assume the mass of the proton as mP and the charge on it as e.
(a) After a long time, when the potential of the sphere reaches a constant value, sketch the trajectory of proton in the beam. (b) Once the potential of the sphere has reached its final, constant value, find the minimum speed v of a proton along its trajectory path. (c) Find the limiting electric potential of the sphere.
View SolutionWhat is the excess charge on a conducting sphere of radius r = 0.35 m if the potential of the sphere is 1500 V and V = 0 at infinity ?
View SolutionA conducting sphere is enclosed by a hollow conducting shell. Initially the inner sphere has a charge Q while the outer one is uncharged. The potential difference between the two spherical surface is found to be V. later on the outer shell is given a charge -4Q. The new potential difference between the two surfaces is : (A) V (B) −V (C) −2V (D) 2V
View SolutionMetallic sphere of radius R is charged to potential V. Then charge q is proportional to
View Solution

