In order to increase the resistance of a given wire of unknown of uniform cross section to four times its value, a fraction of its length is stretched uniformly till the full length of the wire becoes 32 times the original length. What is the value of this fraction?
A
14
B
18
C
116
D
16
Video Solution
Text Solution
The correct Answer is:B
Suppose n(<1) fraction of length is stretched to m times.
Then, (1−n)l+(nl)m=1.5l
or nm−n=0.5
R=ρlA=ρlV/l(V=volume)
=ρl2V
R∝l2 (if V=constant)
Now the second condition is
(1−n)R+(nR)m3=4R
:.m2−n=3 ...........iii
Solving these two equations, we get
n=18
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:DC PANDEYChapter:CURRENT ELECTRICITYExercise:Level 2 More Than One Correct
Explore 10 Videos
- CURRENT ELECTRICITYBook:DC PANDEYChapter:CURRENT ELECTRICITYExercise:Level 2 Comprehension Example Type
Explore 2 Videos
- CURRENT ELECTRICITYBook:DC PANDEYChapter:CURRENT ELECTRICITYExercise:Level 1 Subjective
Explore 53 Videos
- COMMUNICATION SYSTEMBook:DC PANDEYChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrances gallery
Explore 25 Videos
Similar Questions
Knowledge Check
A wire of resistance 12Ω is stretched uniformly till its length becomes three times original length. The change in resistance of wire is
A96ΩB108ΩC150ΩD208ΩIn order to quadruple the resistance of a uniform wire, a part of its length was uniformly stretched till the final length of the entire wire was 1.5 times the original length, the part of the wire was fraction equal to
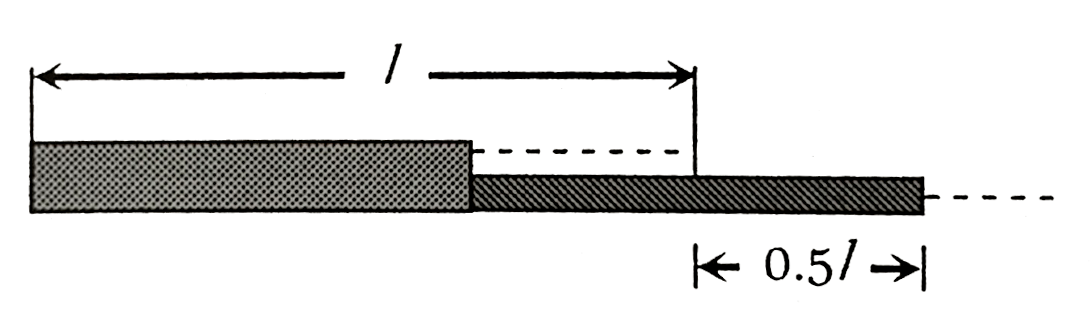 A1/8B1/6C1/10D1/4
A1/8B1/6C1/10D1/4If a wire of resistance 25Ω is uniformly stretched until its length becomes three times its original length then its new resistance is
A100ΩB225ΩC2.25ΩD122.5Ω
A copper wire of resistance R0 is strerched till its length is increased to n times of its original length. What will be its new resistance?
View SolutionThe resistance of a wire is R ohm. What will be its new resistance if it is stretched to n times its original length ?
View SolutionIf length of a metallic wire becomes n times, its resistance becomes
View SolutionThe resistance of wire of length l and area of cross-section a is x ohm. If the wire is stretched to double its length, its resistance would become:
View SolutionA given wire is stretched to double its length. How will its resistance change ?
View Solution