In the circuit in figure E1=3V,E2=2V,E3=1V and R=r1−r2−r3=1Ω
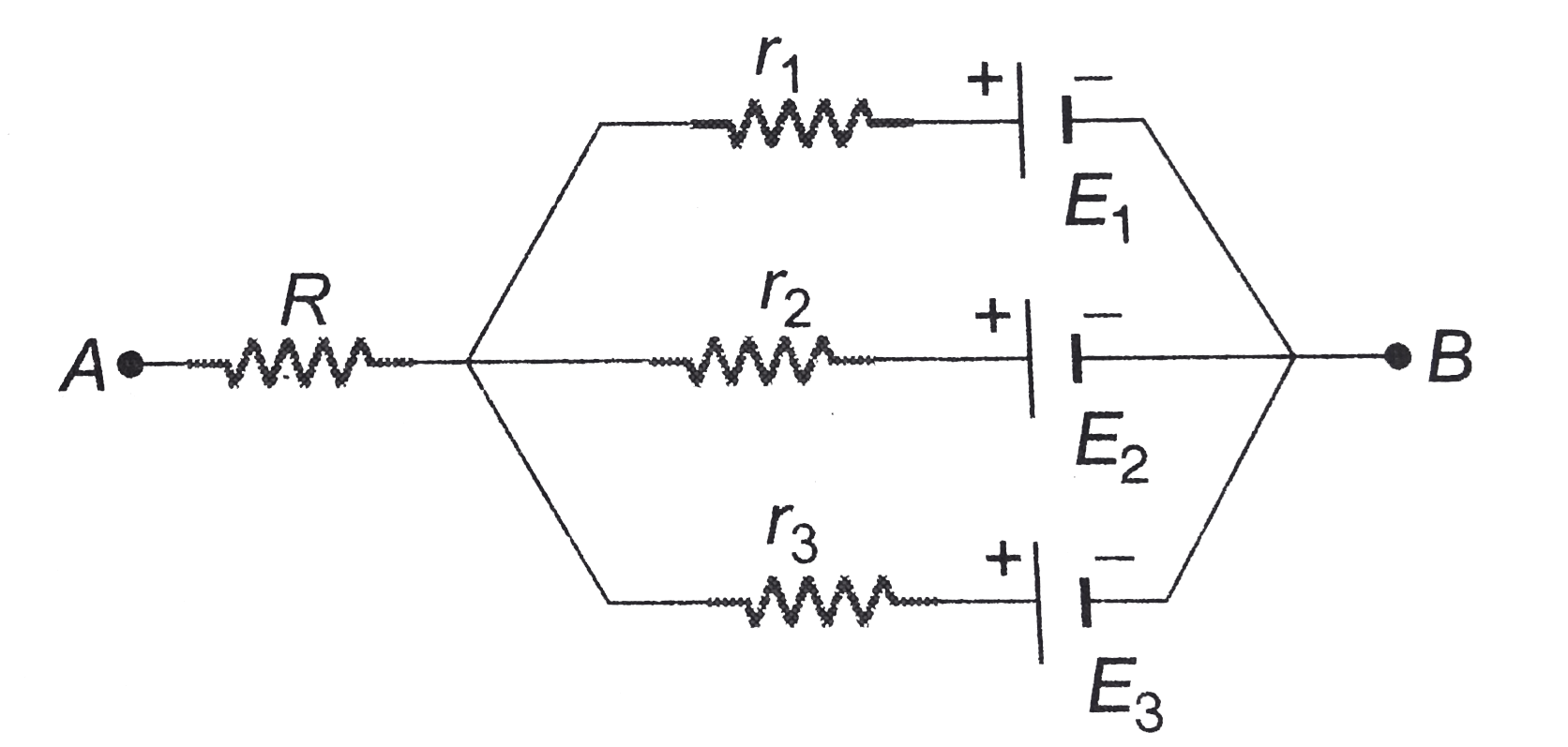
a. Find the potential differece between the points A and B and the currents through each branch.
b. If r2 is short circuited and the point A is connected to point B, find the currents through E1,E2,E3 and the resistor R
a. Equivalent emf of the battries would be
Eeq=Σ(Er)Σ(1r)=(31+21+11)(211+11+11)=2V
Further r1,r2 and r3 each are of 1Ω. Therefore, internal resistance of the equivalent battery will be 13Ω as alll three are in parallel.

The equivalent circuit is therefore shown in the figure.
Since no current is taken from the battery.
VAB=2V (From V=E−ir)
Further VA−VB=E1−i1r1
∴i1=VB−VA+E1r1=−2+3=1A
Similarly, i2=VB−VA+E2r2=−2+21=0
and i3=VB−VA+E3r3=−2+11=−1A
b. r2 is short circuirted means resistance of this branch becomes zero. Making closed circuit with a battery and resistance R. Applying Kirchhoff's second law in three loops so formed.
3−i1−(i1+i2+i30=0 ..............i
2−(i1+i2+i3)=0.............ii
1−i3−(i1+i2+i3)=0.................iii
From equ. ii i1+i2+i3=2A
∴ Substitutig in equ. i we get i1=1A
Substitution in eq. iii we get i3=−1A
∴i2=2A

Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 1
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 2
1 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
In the circuit shown in fig E1=3vo<s,E2=2vo<s,E3=1vo<andR=r1=r2=r3=1ohm.
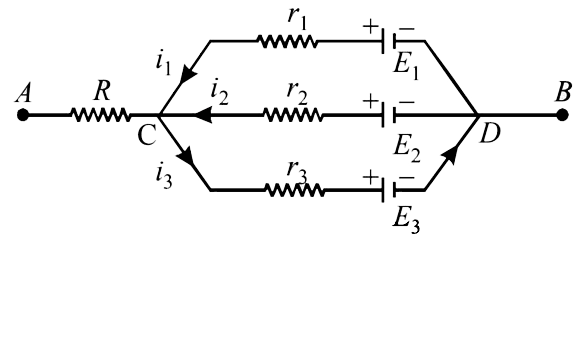
(i) Find the potential difference between the points A and B and the currents through each branch.
(ii) If r2 is short circuited and the point A is connected to point B, find the current through E1,E2,E3 and the resistor R.
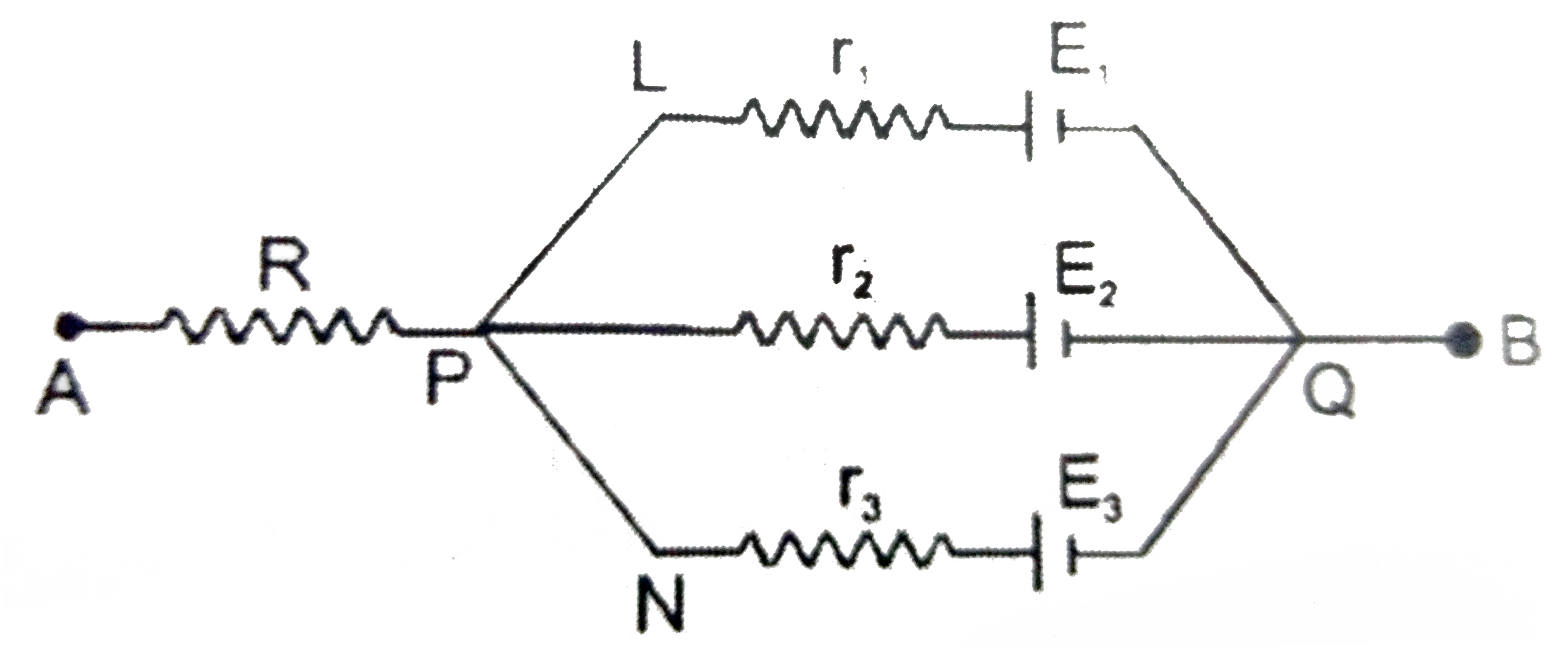
View SolutionIn the circuit shown in fig. E1=3 volt,E2=2 volt,E3=1 vole and R=r1=r2=r3=1ohm.
(i) Find potential difference in Volt between the points A and B with A & B unconnected.
(ii) If r2 is short circuited and the point A is coneted to point B through a zero resistance wire, find the current through R in ampere.
View Solution
Knowledge Check
In the circuit shown in fig. 5.265, E1=E2=E3=2V and R1=R2=4Ω. The current flowing between points A and B through battery E2 is
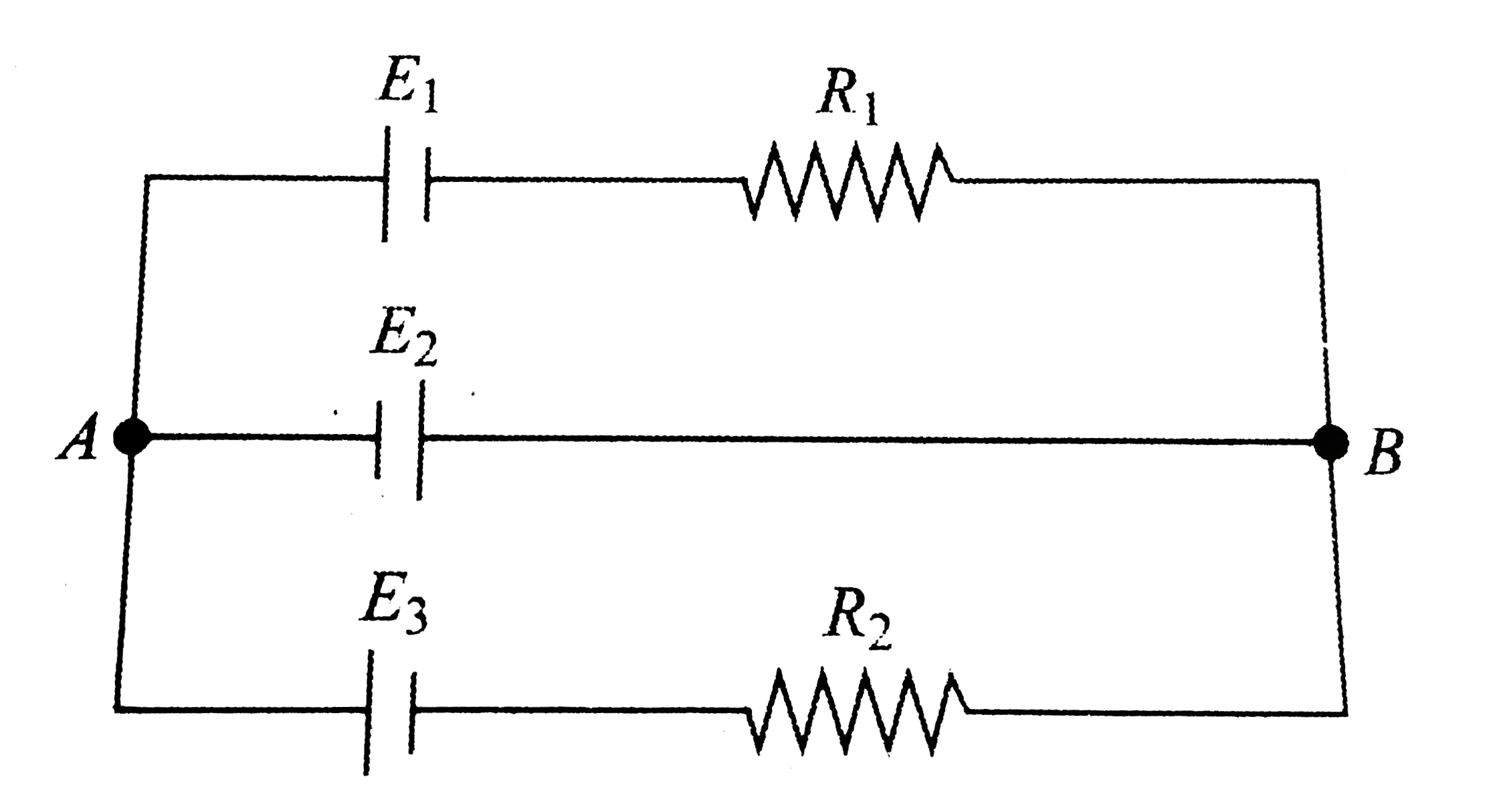 AzeroB2 A from A to BC2 A form B to ADnone of the above
AzeroB2 A from A to BC2 A form B to ADnone of the above
In the circuit shown in figure ,(ε)1=3V,(ε)2=2V,(ε)3=1Vandr1=r2=r3=1(Ω).Find the potential difference between the points A and B and the current through each branch.

View SolutionIn the circuit as shown in figure,
E1=2V,E2=2V,E3=1V,andR=r1=r2=r3Ω.
The potential difference between points A and B will be

View SolutionIn the circuit shown in figure ,(ε)1=3V,(ε)2=2V,(ε)3=1Vandr1=r2=r3=1(Ω).Find the potential difference between the points A and B and the current through each branch.

View SolutionIn the circuit shown in figure
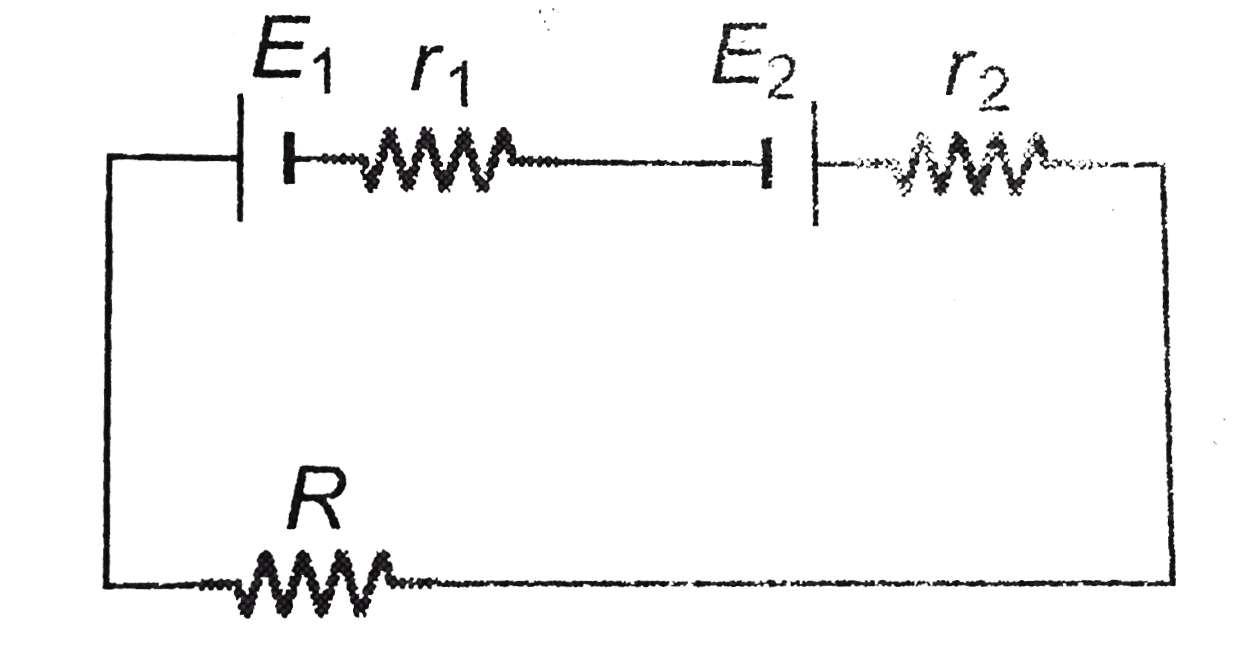
E1=10V,E2=4V,r1=r2=1Ω and R=2Ω.
Find the potential difference across battery 1 and battery 2.
View SolutionIn the circuit shown in fig. E1=3 volt,E2=2 volt,E3=1 vole and R=r1=r2=r3=1ohm.
(i) Find potential difference in Volt between the points A and B with A & B unconnected.
(ii) If r2 is short circuited and the point A is coneted to point B through a zero resistance wire, find the current through R in ampere.

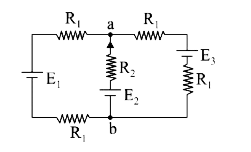
View SolutionFor the circuit shown, with R1=1.0Ω,R2=2.0Ω,E1=2VandE2=E3=4V the potential difference between the points ‘a’ and ‘b’ is __________(in V)
View SolutionIn the following circuit E1=E2=E32V and R1=R2=AΩ. The current passing through battery E2 between points A and B is
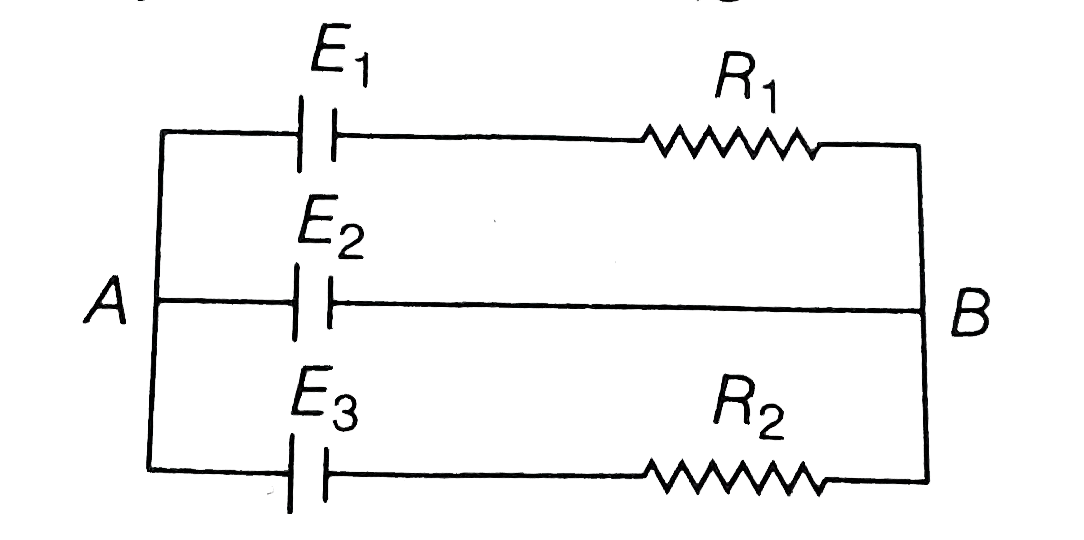
View Solution
