One end of a copper rod of length 1 m and area of cross - section 400×(10−4)m2 is maintained at 100∘C. At the other end of the rod ice is kept at 0∘C. Neglecting the loss of heat from the surrounding, find the mass of ice melted in 1h. Given, KCu=401W/m−KandLf=3.35×(105)J/kg.
The correct Answer is:A, B
Thermal resistance of the rod

R=lKA=1.0(401)(4×(10−4))=6.23K/W
∴ Heat current , H=Temperature differenceThermal resistance
=(100−06.23)=16W
Heat transferred in 1 h,
Q=Ht⟨.H=Qt)
=(16)(3600)=57600J
Now, let m mass of ice melts in 1 h, then
m=QL
=576003.35×(105)
=0.172
or =172g .
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Exercise 22.1
7 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Exercise 22.2
7 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Example Type 4
4 Videos
- BASIC MATHEMATICSBOOK - DC PANDEYCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
One end of a copper rod of length 1m and area of cross section 4.0×10−4m2 is maintained at 100∘C. Neglecting the loss of heat to the surroundings find the mass ice melted in 1 hour. Given KCu=401 watt/m - k and Lf=3.35×105J/kg.

View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View Solution
Knowledge Check
One end of a metal rod of length 1.0 m and area of cross section 100cm2 is maintained at . 100∘C. If the other end of the rod is maintained at 0∘C , the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod =100W/m−K)
A3×103JB6×103JC9×103JD12×103JThe ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK
 AThe temperature of rod at centre is 250∘CBThe temperature of rod at centre is 50∘CCThe temperature gradient in right half is 500∘C/mDThe temperature gradient in left half is 300∘C/m
AThe temperature of rod at centre is 250∘CBThe temperature of rod at centre is 50∘CCThe temperature gradient in right half is 500∘C/mDThe temperature gradient in left half is 300∘C/mA heat flux of 4000 J/s is to be passed through a copper rod of length 10 cm and area of cross section 100cm2. The thermal conductivity of copper is 400W/m/∘C The two ends of this rod must be kept at a temperature difference of
A1∘CB10∘CC100∘CD1000∘C
One end of a steel rod of length 1 m and area of cross section 4×10−6m2 is put in boiling water and the other end is kept in an ice bath at 0∘C. If thermal conductivity of steel is 46W/m∘C, find the amount of ice melting per second if heat flow only by conduction. Given that the latent heat of fusion of ice is 3.36×105J/kg.
View SolutionOne end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
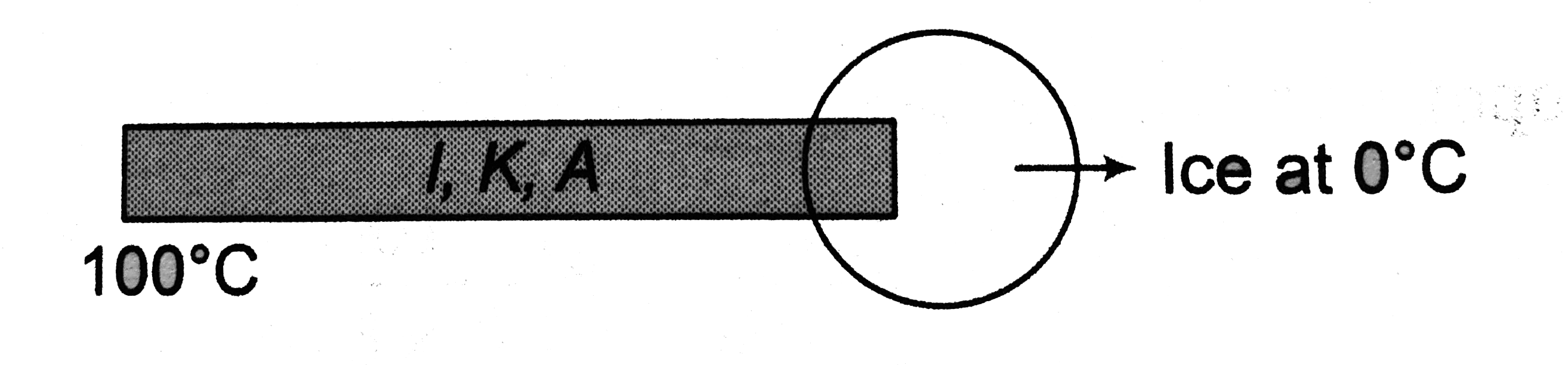 .
.
View SolutionOne end of a brass rod of length 2.0 m and cross section 1cm2 is kept in stream at 100∘C and the other end in ice at 0∘C. The lateral suface of the rod is covered by heat insulator. Determine the amount of ice melting per minute. Thermal conductivity of brass is 110W/m−K and specific latent heat of fusion of ice is 80cal/g.
View SolutionOne end of a copper rod of length 0.25m and area of cross-section 10−4m2 is immersed in a liquid boiling at 125∘C whereas the other end is kept cold by dipping It in an ice-cold bath. Find (i) temperature gradient, (ii) the rate of heat transfer (iii) the temperature at a point 0.1m from the higher temperature end. (λ of copper =92cals−1m−1K−1)
View SolutionOne end of a copper rod of length 1.0 m and area of cross-section 10−3 is immersed in boiling water and the other end in ice. If the coefficient of thermal conductivity of copper is 92cal/m−s−.∘C and the latent heat of ice is 8×104cal/kg, then the amount of ice which will melt in one minute is
View Solution
