An ideal monoatomic gas undergoes a process in which its internal energy U and density ρ vary as Uρ= constant. The ratio of change in internal energy and the work done by the gas is
(a) 32
(b) 23
(c) 13
(d) 35
The correct Answer is:A
To solve the problem, we need to find the ratio of the change in internal energy (ΔU) to the work done (W) by an ideal monoatomic gas undergoing a process where the product of internal energy (U) and density (ρ) is constant.
1. Understand the relationship: Given that U⋅ρ=constant, we can express this as:
U=Cρ
where C is a constant.
2. Express internal energy in terms of density: For an ideal monoatomic gas, the internal energy U is related to temperature T by:
U=32nRT
where n is the number of moles and R is the universal gas constant.
3. Relate temperature to density: Since U is proportional to 1ρ, we can also express temperature as:
T∝1ρ
This implies that as the density increases, the temperature decreases.
4. Using the ideal gas law: The ideal gas law states:
PV=nRT
Since ρ=mV and mass m is constant, we can say:
ρ∝1V⟹V∝1ρ
5. Establish the relationship between T and V: From the previous steps, we have:
T∝V
6. Work done by the gas: The work done by the gas at constant pressure can be expressed as:
W=PΔV
Using the ideal gas law, we can relate pressure to temperature and volume:
P=nRTV
7. First Law of Thermodynamics: According to the first law,
ΔU=Q−W
For a process at constant pressure, the heat added Q can be expressed as:
Q=nCpΔT
8. Expressing ΔU and W:
- The change in internal energy for a monoatomic gas is:
ΔU=nCvΔT
- The work done is:
W=nCpΔT−ΔU
9. Finding the ratio: Now we can find the ratio of change in internal energy to work done:
ΔUW=nCvΔTnCpΔT−nCvΔT
Simplifying gives:
ΔUW=CvCp−Cv
For a monoatomic ideal gas, we know:
Cp−Cv=R
Thus,
ΔUW=CvR
10. Substituting the values: For a monoatomic gas, Cv=3R2:
ΔUW=3R2R=32
Final Answer:
The ratio of change in internal energy to the work done by the gas is:
ΔUW=32
U=Cρ
where C is a constant.
U=32nRT
where n is the number of moles and R is the universal gas constant.
T∝1ρ
This implies that as the density increases, the temperature decreases.
PV=nRT
Since ρ=mV and mass m is constant, we can say:
ρ∝1V⟹V∝1ρ
T∝V
W=PΔV
Using the ideal gas law, we can relate pressure to temperature and volume:
P=nRTV
ΔU=Q−W
For a process at constant pressure, the heat added Q can be expressed as:
Q=nCpΔT
- The change in internal energy for a monoatomic gas is:
ΔU=nCvΔT
- The work done is:
W=nCpΔT−ΔU
ΔUW=nCvΔTnCpΔT−nCvΔT
Simplifying gives:
ΔUW=CvCp−Cv
For a monoatomic ideal gas, we know:
Cp−Cv=R
Thus,
ΔUW=CvR
ΔUW=3R2R=32
The ratio of change in internal energy to the work done by the gas is:
ΔUW=32
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 More Than One Correct6videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Passage I2videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 1 Subjective24videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery39videos
LAWS OF MOTION
- BOOK - DC PANDEYCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions10videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
Similar Questions
An ideal monoactomic gas undergoes a process ini which its internal energy depends upon its volume as
U=a√V [where a is a constant]
(a) find work done by a gas and heat transferred to gas to increse its internal energy by 200 J.
(b) find molar specific heat of gas for this process.View SolutionAn ideal diatomic gas (γ=75) undergoes a process in which its internal energy relates to the volume as U=α√V, where α is a constant.
(a) Find the work performed by the gas to increase its internal energy by 100J.
(b) Find the molar specific heat of the gas.View Solution
Knowledge Check
- Question 1 - Select One
In an isothermal expansion change in internal energy and work done by the gas are respectively
A(-) ve, (-) veB0, (+) veC0, (-) veD(+) ve, (-) ve - Question 2 - Select One
In an isothermal expansion change in internal energy and work done by the gas are respectively
A(-)ve, (-) yeB0, (+)veC0,(-)veD(+) ve, (-) ve - Question 3 - Select One
Change in internal energy in an isothermal process for ideal gas is
AZeroB(+) veC(-) veDCannot be predicted
An ideal gas with the adiabatic exponent γ undergoes a process in which its internal energy relates to the volume as u=aVα. Where a and α are constants. Find :
(a) the work performed by the gas and the amount of heat to be transferred to this gas to increase its internal energy by ΔU ,
(b) the molar heat capacity of the gas in this process.View SolutionAn ideal gas with the adiabatic exponent γ undergoes a process in which its internal energy relates to the volume as U=aVα, where a and α are constants. Find the work performed by the gas and the amount of heat to be transferred to this gas to increase its internal energy by ΔU
View SolutionTwo moles of an ideal monoatomic gas undergo a cyclic process which is indicated on a P−U diagram, where U is the internal energy of the gas. The work done by the gas in the cycle is k×102In2. Find k.
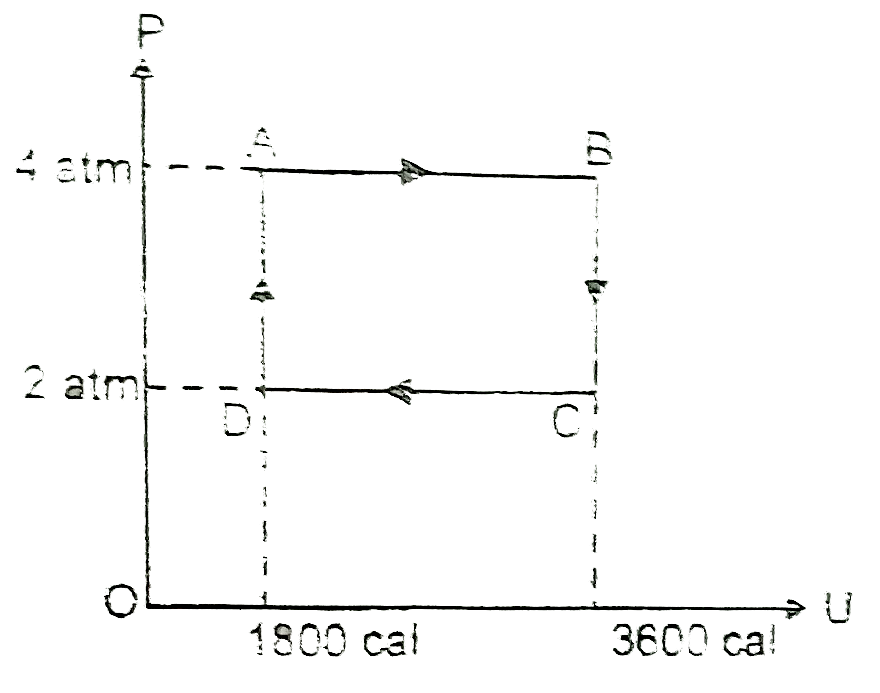 View Solution
View SolutionThe internal energy of a perfect monoatomic gas is
View SolutionInternal energy of ideal gas depends on
View Solution

