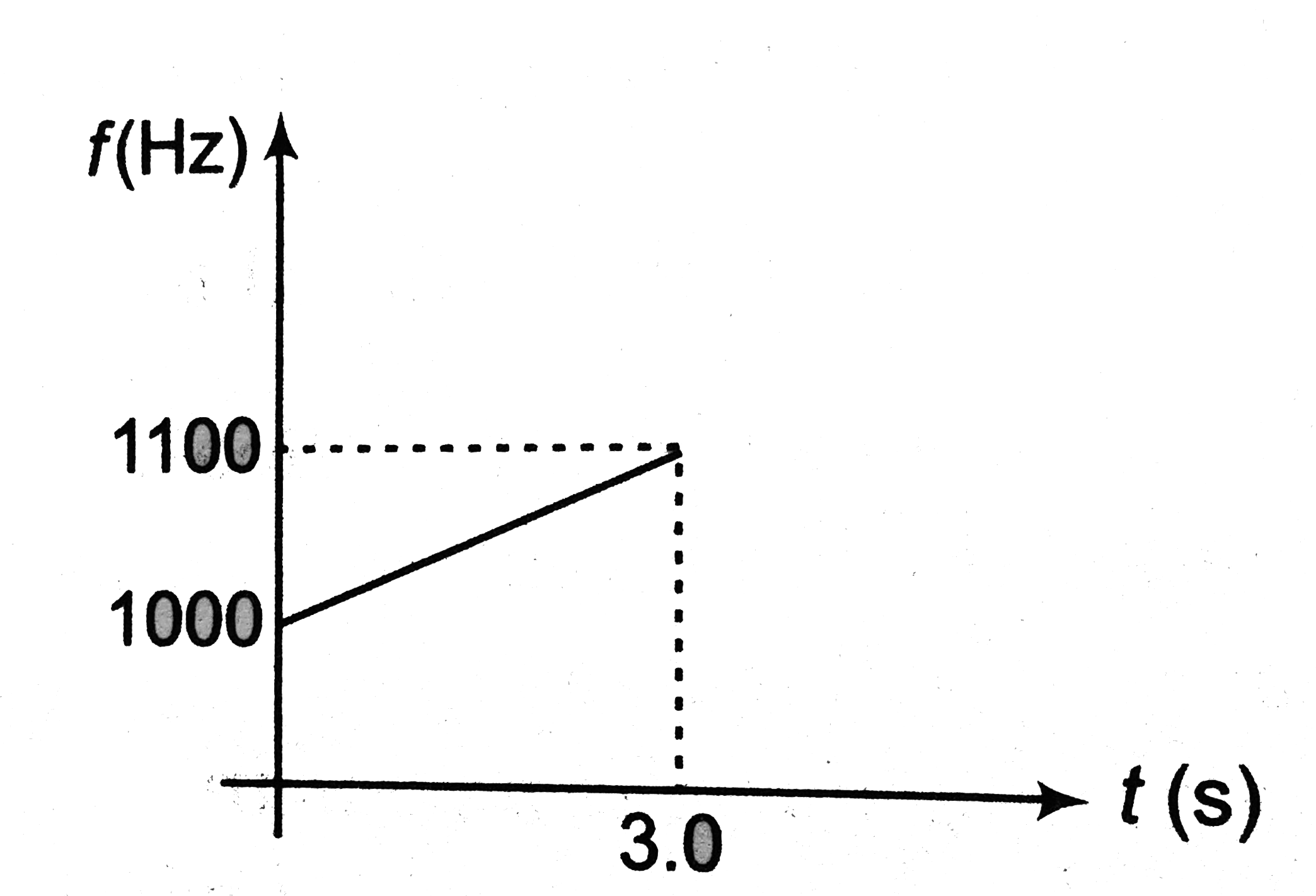
A detector is released from rest over a source of sound of frequency fo=103HZ. The frequency observer by the decector at time t is plotted in the graph. The speed of sound in air (g=10m/s2)
330m/s
350m/s
300m/s
310m/s
The correct Answer is:C
f=fo(ν+νoν)
=103(1+10tν) (as νo=gt)
Hence, f versus t graph is straight line of slope
104ν.
∴104ν= slope =1003
∴ν=300m/s
Topper's Solved these Questions
- SOUND WAVESBook:DC PANDEYChapter:SOUND WAVESExercise:Single correct option
Explore 1 Video
- SOUND WAVESBook:DC PANDEYChapter:SOUND WAVESExercise:Level 2 More Than One Correct
Explore 5 Videos
- SOUND WAVESBook:DC PANDEYChapter:SOUND WAVESExercise:Subjective Questions
Explore 1 Video
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
- SUPERPOSITION OF WAVESBook:DC PANDEYChapter:SUPERPOSITION OF WAVESExercise:Level 2 Subjective
Explore 8 Videos
Similar Questions
A source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionA source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170ms−1. A detector is placed at a distance of 200 m from the line of motion of the source. (a) Find the frequency of sound received by the detector at the instant when the source gets closest to it. (b) Find the distance between the source and the detector at the instant it detects the frequency 1200 Hz. Velocity of sound in air=340ms−1.
View Solution
Knowledge Check
A detector is released from rest over a source of sound of frequency f0=103Hz. The frequency observed by the detector at time t is plotted in the graph. The speed of sound in air is (g=10m/s2)
 A330m/sB350 m/sC300 m/sD310 m/s
A330m/sB350 m/sC300 m/sD310 m/sA detector is released from rest over height h a source of sound of frequency f0=103Hz. The frequency observed by the detector at time t is plotted in the graph. The speed of sound in air is (g=10m/s2)
_E01_060_Q01.png) A330 m/sB350 m/sC300 m/sD310 m/s
A330 m/sB350 m/sC300 m/sD310 m/s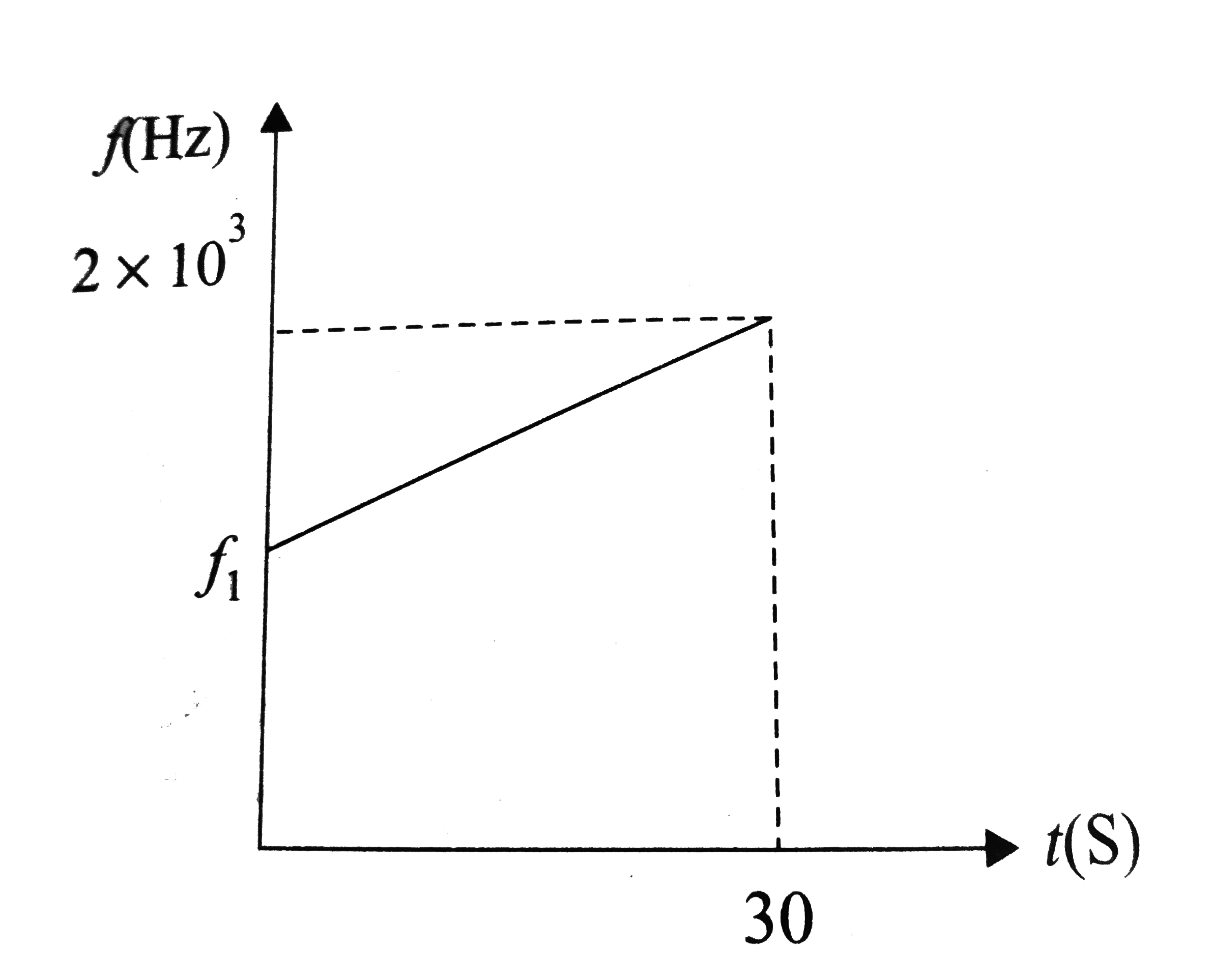
A source of sound of frequency f1 is placed on the ground. A detector placed at a height is released from rest on this source. The observed frequency f(Hz) is plotted against time t(sec) . The speed of sound in air is 300ms. Find f1 (g=10ms).A0.5×103HzB2×103HzC0.25×103HzD0.2×103Hz
One train is approaching an observer at rest and another train is receding from him with the same velocity 4m/s . Both trains blow whistles of same frequency of 243HZ . The beat frequency in HZ as heard by observer is (speed of sound in air = 320m/s)
View SolutionA source emits sound of frequency 600Hz inside water. The frequency heard in air will be equal to (velocity of sound in water=1500ms, velocity of sound in air=300(m)/(s))
View SolutionThe source of sound generating a frequency of 3 kH z reaches an observer with a speed of 0.5 times the velocity of sound in air. The frequency heard by the observer is
View Solution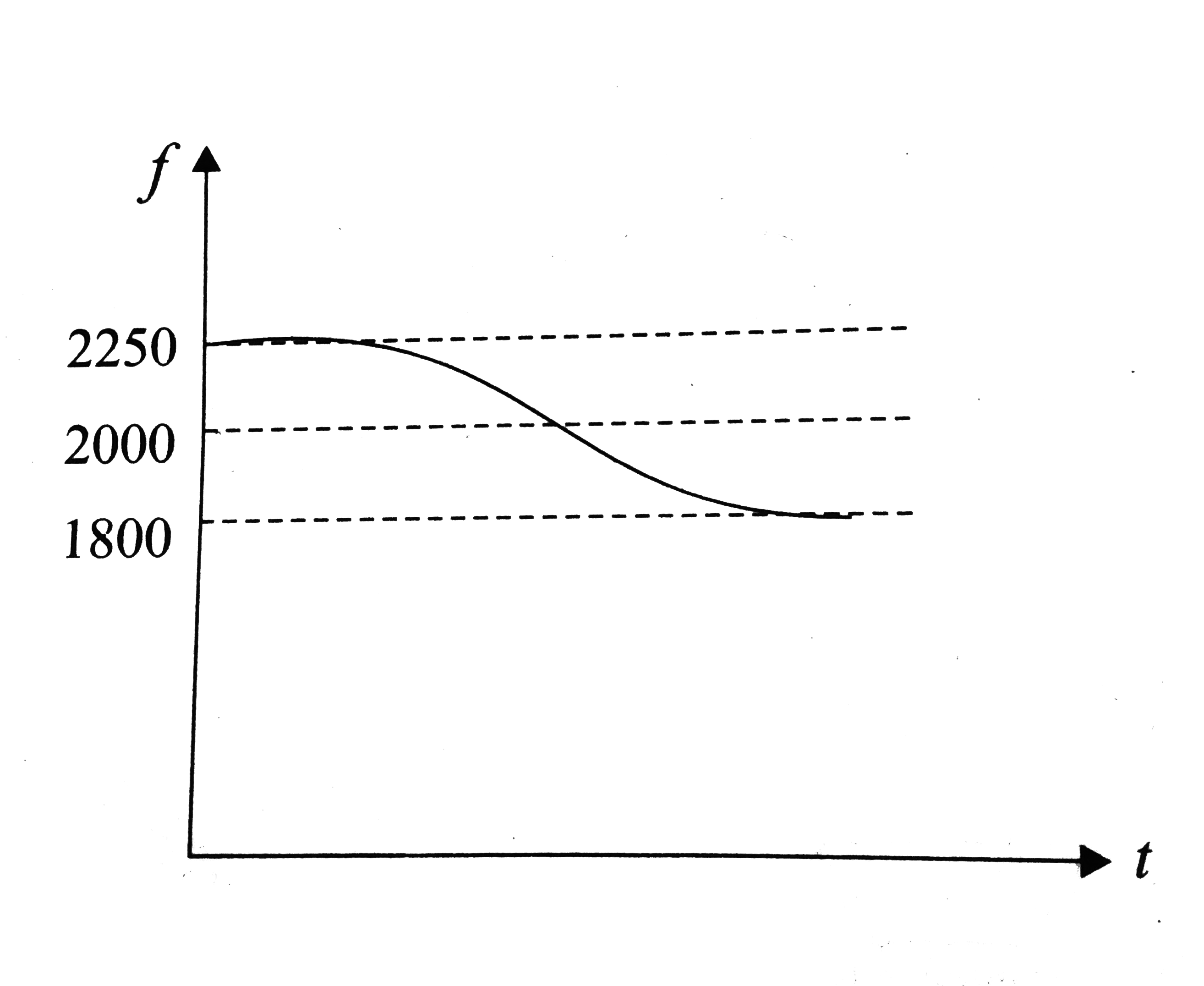
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300ms
View SolutionA source of sound is travelling towards a stationary observer. The frequency of sound heard by the observer is 25% more than the actual frequency. If the speed of sound is v, that of the source is
View Solution

