A wire of length 40cm which has a mass of 4 g oscillates in its second harmonic and sets the air column in the tube to vibrations in its funrations in its fundamental mode as shows in figure. Assuming the speed of sound in air as 340m/s . Find the tension in the wire. 
The correct Answer is:A
2(ν2l1)=(ν24l2)
or √T/μl1=(ν24l2)
∴T=μ(ν2l14l2)2
=(4×10−30.4)(340×404×100)2
=11.56N
Topper's Solved these Questions
- SOUND WAVESBOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Subjective Questions
1 Videos
- SOUND WAVESBOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Level 2 Single Correct
14 Videos
- SOUND WAVESBOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Level 1 Objective
34 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
Similar Questions
Consider the situation shown in figure. The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 40ms−1, find the tension in the wire.
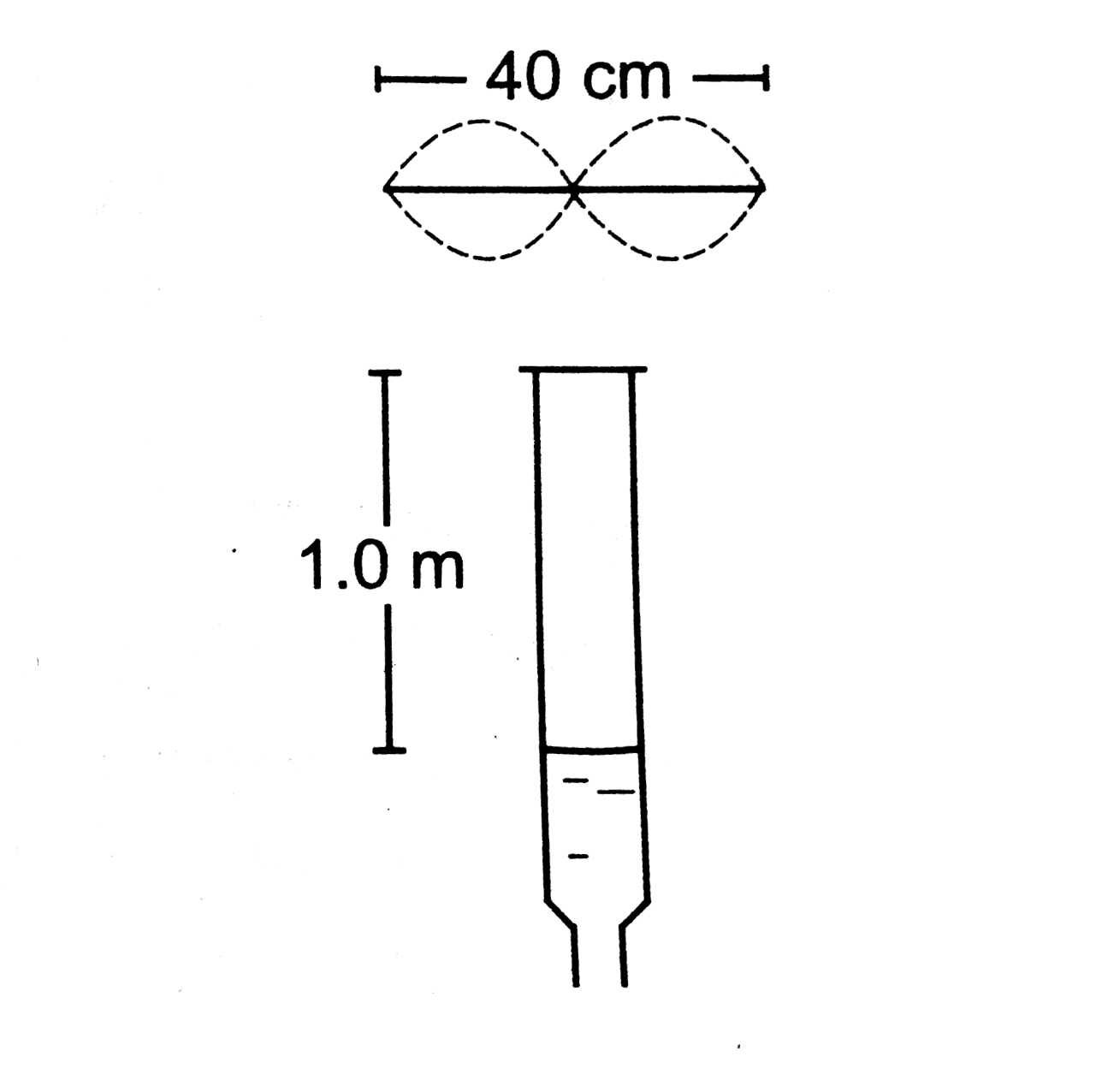 .
.
View SolutionA tube 1.0m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3m long and a mass of 0.01kg . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find
(a) the frequency of oscillation of the air column and
(b) the tension in the wire.
Speed of sound in air = 330m/s .
View Solution
Knowledge Check
A whistle whose air column is open at both ends has a fundamental frequency of 5100 Hz. If the speed of sound in air is 340 ms−1, the length of the whistle, in cm, is
A5/3B10/3C5D20/3Length of 0.3m wire vibrates in fundamental mode at frequency 480 Hz. The velocity of sound wave in air is
A330 m/sB320 m/sC330 m/sD288 m/sLength of 0.3 m wire vibrates in fundamental mode at frequency 480Hz. Then the velocity of sound wave in air is
A330m/sB320m/sC300m/sD288m/s
The air column in a pipe closed at one end is made to vibrate in its second overtone by a tuning fork of frequency 440 Hz. The speed of sound in air is 330 m/s. find the length of air column.
View SolutionThe separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340ms−1, find the frequency of vibration of the air column.
View SolutionA tube 1.0m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3m long and a mass of 0.01kg . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find
(a) the frequency of oscillation of the air column and
(b) the tension in the wire.
Speed of sound in air = 330m/s .
View SolutionFind the fundamental, first overtone and second overtone frequencies of an open organ pipe of length 20 cm. Speed of sound in air is 340ms−1.
View SolutionA string 25cm long and having a mass of 2.5gm is under tension. A pipe closed at one end is 40cm long. When the string is set vibrating in its first overtone and the air in the pipe in its fundamental frequency, 8 beats per second are heard. It is observed that decreasing the tension in the string decreases beat frequency. if the speed of sound in air is 320m/s, find the tension in the string.
View Solution
