Two harmonic waves are represented in SI units by
$y_{1} (x, t) = 0.2 sin (x - 3.0 t) and y_{2} (x, t) = 0.2 sin (x - 3.0 t + ϕ)$
(a) Write the expression for the sum $y = y_{1} + y_{2} f or ϕ = \frac{π}{2} r a d .$
(b) Suppose the phase difference $ϕ$ between the waves is unknown and the amplitude of their sum is 0.32 m, what is $ϕ$ ?

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

(a) $y = y_{1} + y_{2}$
$= 0.2 sin (x - 3.0 t) + 0.2 sin (x - 3.0 t + \frac{π}{2})$
$= A sin (x - 3.0 t + θ)$

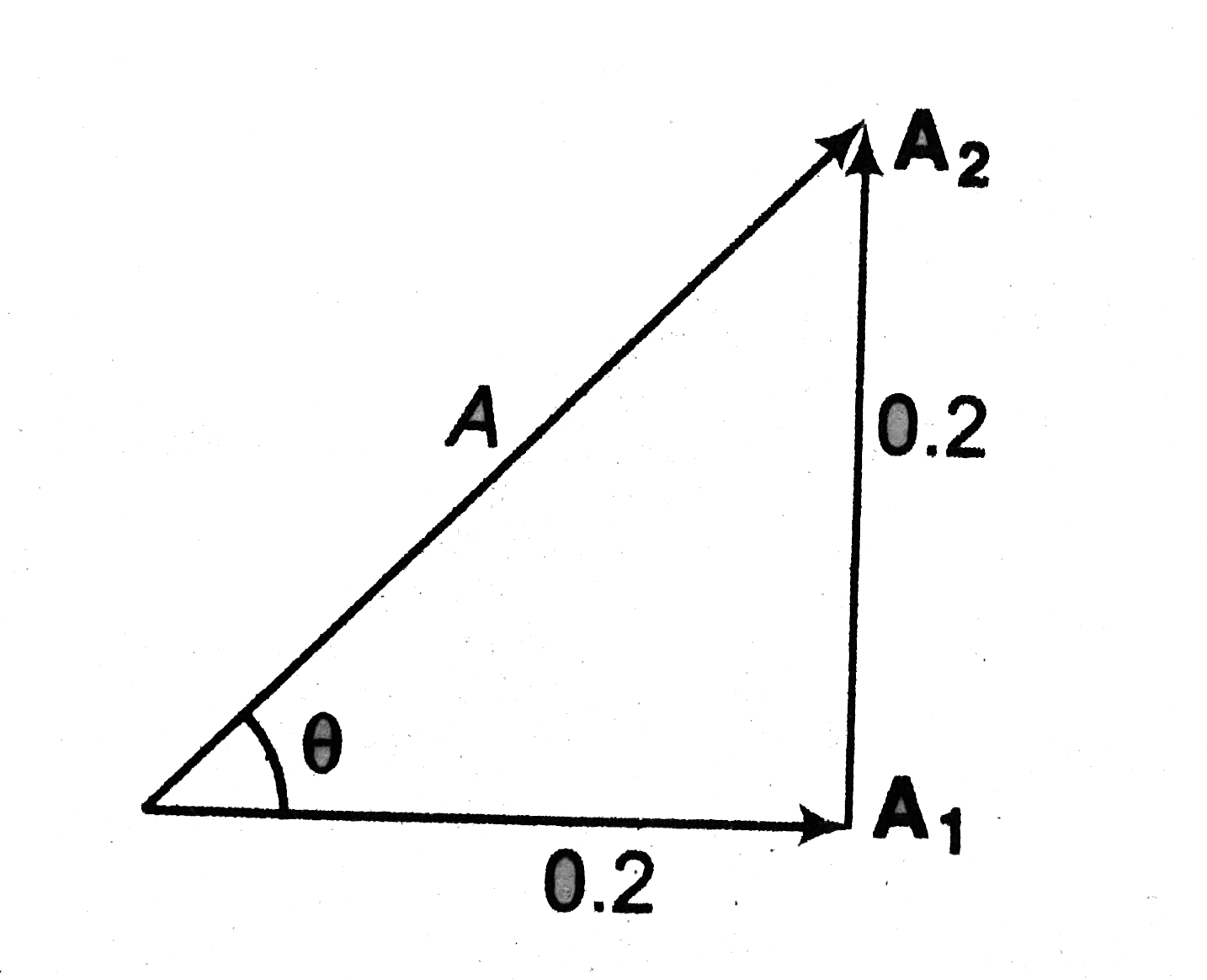
Here, A $= \sqrt{{(0.2)}^{2} + {(0.2)}^{2}}$
and $θ = \frac{π}{4}$
$∴ y = 0.28 sin (x - 3.0 t + \frac{π}{4})$
(b) Since, the amplitude of the resulting wave is
$0.32 m and A = 0.2 m$ , we have
$0.32 = \sqrt{{(0.2)}^{2} + {(0.2)}^{2} + (2) (0.2) (0.2) cos ϕ}$
Solving this, we get
$ϕ = \pm 1.29$ rad .

Updated on:21/07/2023

|

Class 11 PHYSICS TRAVELLING WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

If two waves are represented by :
$y_{1} = 2 sin (4 x - 300 t) & y_{2} = sin (4 x - 300 t - 0.2)$
then their superposed wave will have angular frequency -
A $150 / π$
B $150 π$
C300
D $600 π$
Two simple harmonic waves are represented by the equations given as
$y_{1} = 0.3 sin (314 t - 1.57 x)$
$y_{2} = 0.1 sin (314 t - 1.57 x + 1.57)$
where $x, y_{1}$ and $y_{2}$ are in metre and t is in second, then we have
A $v_{1} = v_{2}$ = 50 Hz
B $λ_{1} = λ_{2}$ = 4 m
CRatio of intensity is 9
D $y_{2}$ leads $y_{1}$ by a phase of $\frac{π}{2}$
Two simple harmonic motion are represented by equations
$y_{1} = 4 sin (10 t + ϕ)$
$y_{2} = 5 cos 10 t$
What is the phase difference between their velocities ?
A $ϕ$
B $- ϕ$
C $(ϕ + \frac{π}{2})$
D $(ϕ - \frac{π}{2})$

DC PANDEY-SUPERPOSITION OF WAVES-Level 1 Subjective

Home
Ask Doubt
Profile