A triangular wave pulse moving at 2 cm/s on a rope approached an end at which it is free to slide on a vertical pole.

(a) Draw the pulse at 12s interval until it is completely reflected.
(b) What is the particle speed on the trailing edge P at the instant depicted?
(Reflection of pulse from a free boundry is really the supperposition of two
identical waves travelling in opposite direction. This can be shown as under.
 ,
,

In every 1/2s, each pulse (one real moving towards right and one imaginary moving towards left) travels a distance of 1cm as the wave speed is 2 cm/s.
(b) Particle speed, vp=|−v(slope)|
Here, v=wave speed =2cm/s
and slope =1/2
∴Particle speed=1cms .
Topper's Solved these Questions
- SUPERPOSITION OF WAVESBook:DC PANDEYChapter:SUPERPOSITION OF WAVESExercise:miscellaneous example
Explore 7 Videos
- SUPERPOSITION OF WAVESBook:DC PANDEYChapter:SUPERPOSITION OF WAVESExercise:Exercise 18.1
Explore 3 Videos
- SUPERPOSITION OF WAVESBook:DC PANDEYChapter:SUPERPOSITION OF WAVESExercise:Example Type 3
Explore 1 Video
- SOUND WAVESBook:DC PANDEYChapter:SOUND WAVESExercise:Exercise 19.7
Explore 4 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBook:DC PANDEYChapter:THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESExercise:Medical entrance gallary
Explore 30 Videos
Similar Questions
Two triangular wave pulses are travelling toward each other on a stretched string as shown in Fig . 7.25. Both pulses are identical to each other and travels at 2.00cm/s. The leading edges of the pulses are 1.00cmapart at t=0 . Sketch the shape of the string at t=0.250s,t=0.500s,t=0.750s,t=1.000sandt=1.250s.
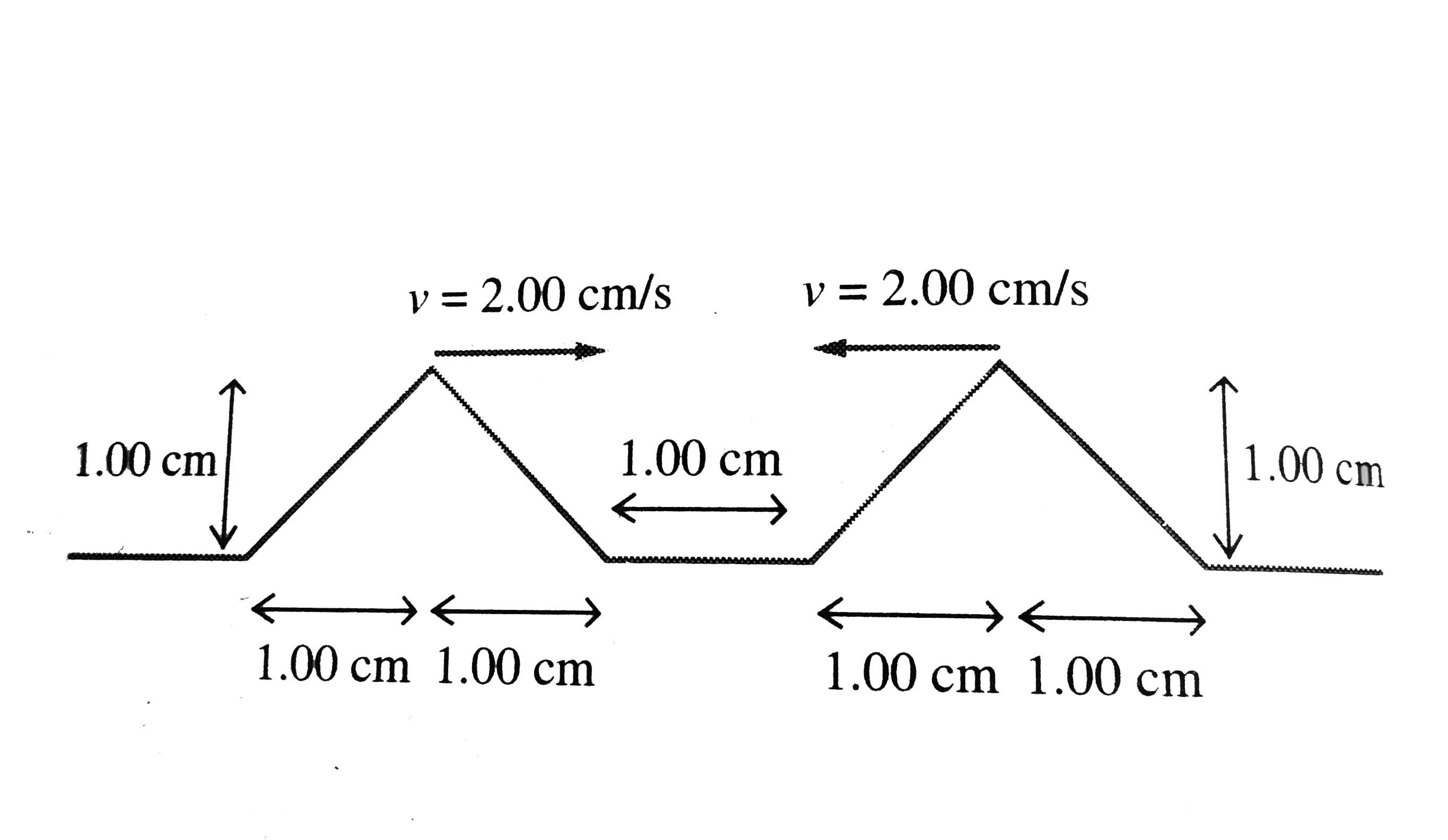
View SolutionA string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?

View Solution
Knowledge Check
A wave pulse on a string has the dimension shown in figure.
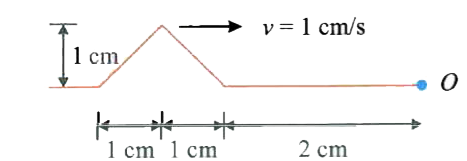
The wave speed is v=1cm/s. If point O is free end. The shape of wave at time t=3s isA B
B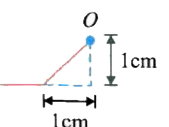 C
C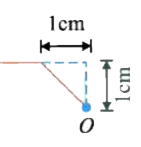 D
D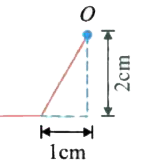
A wave pulse on a string has the dimension shown in figire. The waves speed is v=1cm/s If point O is a free end. The shape of wave at time t=3s is :-
_E01_021_Q01.png) .A
.A_E01_021_O01.png) B
B_E01_021_O02.png) C
C_E01_021_O03.png) D
D_E01_021_O04.png)
A wave pulse moving through air causes change in the density of air. The variation of density at two different instants are shown in the figure. The figure (a) corresponds to, t=10s and figure (b) to t=10 s.
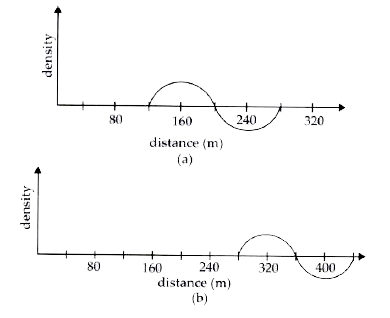 The speed of the wave pulse isA520m s−1B320m s−1C300m s−1D220m s−1
The speed of the wave pulse isA520m s−1B320m s−1C300m s−1D220m s−1
A 4.0kg block is suspended from the celling of an elevator through a string having a linear mass density of 1.6×10−2kg/m. Find (a) speed (with respect to the string) with which pulse can proceed on the string it he elevator accelerates up at the rate of 6m/s. (b) in part (a) at some instant speed of lift is 40m/s in upward direction, then speed of the wave pulse with respect to ground at that instant is (Take =10m/s2)
View SolutionA wave pulse is travelling on a string at 2 m/s. displacement y of the particle at x = 0 at any time t is given by
y=2t2+1
Find
(ii) Shape of the pulse at t = 0 and t = 1s.
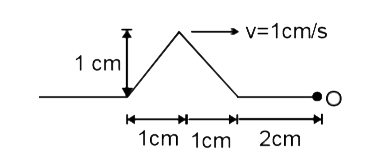
View SolutionA Wave pulse on a string has the dimension shown in figure. The waves speed is v=1 cm/s. If point O is a free end. The shape of wave at time t=3 s is:
View SolutionThe speed-time graph of a particle moving along a fixed direction is shown in figure. Obtain the distance traversed by the particle between (a)t=0s to 10s(b)t=2s to 6s
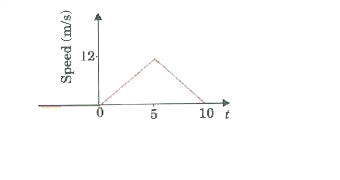
What is the average speed of the particle over the intervals in a and b?
View SolutionA large wedge BCD, having its inclined surface at an angle θ=45∘ to the horizontal, is travelling horizontally leftwards with uniform velocity u=10m/s
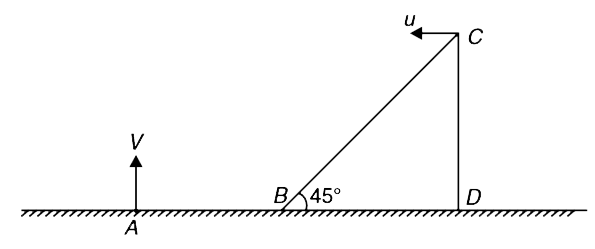
At some instant a particle is projected vertically up with speed V=20m/s from point A on ground lying at some distance right to the lower edge B of the wedge. The particle strikes the incline BC normally, while it was falling. [g=10m/s2]
(a) Find the distance AB at the instant the particle was projected from A.
(b) Find the distance of lower edge B of the wedge from point A at the instant the particle strikes the incline.
(c) Trace the path of the particle in the reference frame attached to the wedge.
View Solution