Question

Three waves from three coherent sources meet at some point. Resultant amplitude of each is $A_0$. Intensity corresponding to $A_{0}is{I}_0$. Phase difference between first wave and second wave is ${60}^{\circ }$. Path difference between first wave and third wave is $\frac{\lambda }{3}$. The first wave lags behind in phase angle from second and third wave. Find resultant intensity at this point.

Answer

D

Explanation

Here, the sources are three. So, we don't have any direct formula for finding the resultant intensity. First we will find the resultant amplitude by vector method and then by the relation `I prop A^2`, we can also find the resulting intensity.
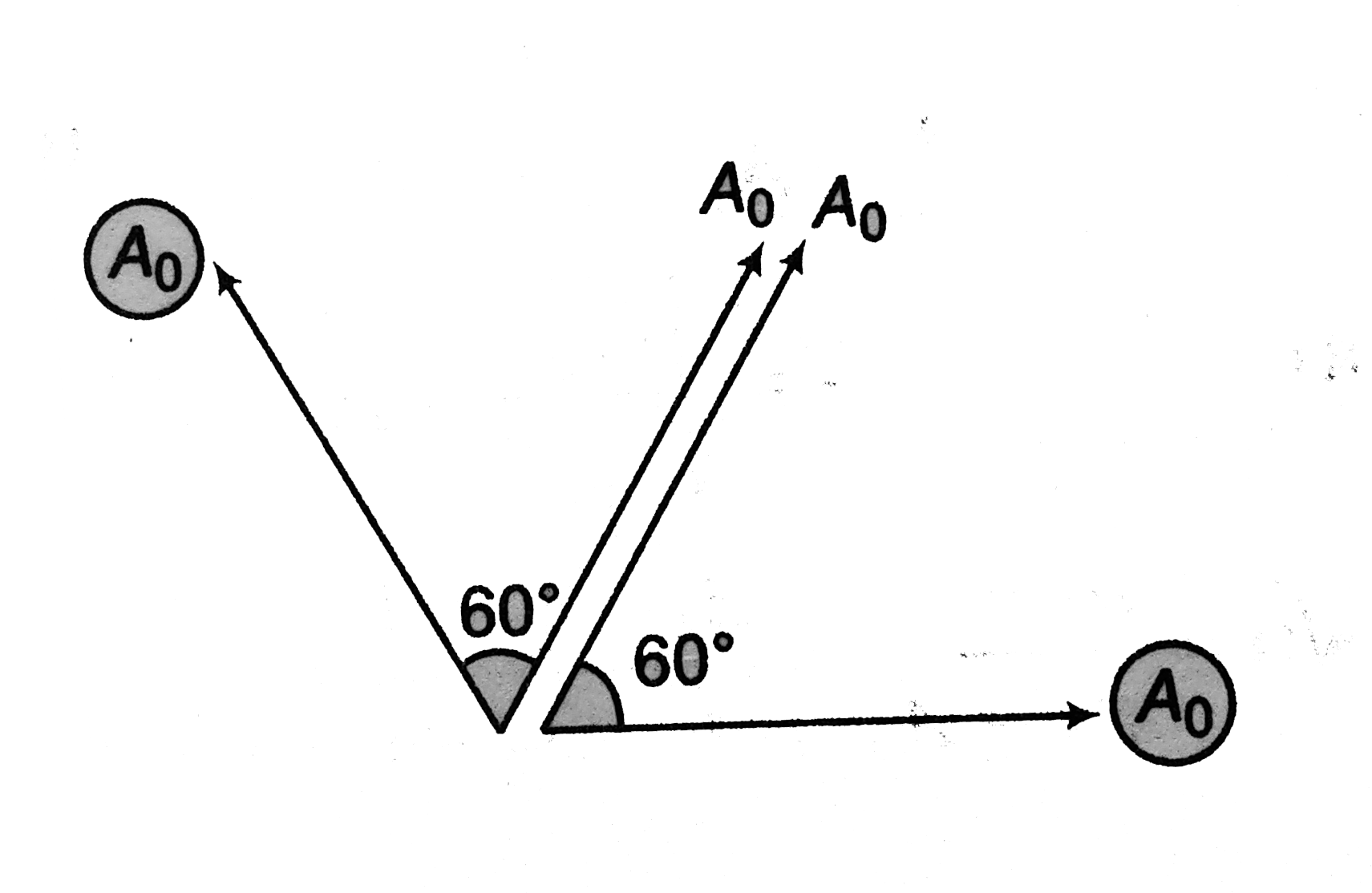
Further, a path difference of `lambda/3` is equivalent to phase difference of `120^@(Delta phi or phi = (2pi)/lambda. Delta x).
Hence, the phase difference first and second is `60^(@)` and between first and third is `120^(@)`. So, vector diagram for amplitude is as shown below.
` (##DCP_V03_C18_S01_002_S01.png" width="80%">
Now, resultant of first and third acting at `120^(@)` is also `A_0` (as `A=2A_(0) (cos) phi/2 and phi=120^@`) and
since the first and third are equal, so this resultant `A_(0)` passes through the bisector line of these two or in the direction of second amplitude vector. Therefore, the resultant amplitude is
`A= A_0 + A_0 = 2A_0`
and the resultant intensity is
`I=4I_0` (as `I prop A^2`).