A ball of density d is dropped on to a horizontal solid surface. It bounces elastically from the surface and returns to its original position in a time t1. Next, the ball is released and it falls through the same height before striking the surface of a liquid of density of dL
(a) If d<dL, obtain an expression (in terms of d, t1 and dL) for the time t2 the ball takes to come back to the position from which it was released.
(b) Is the motion of the ball simple harmonic?
(c) If d=dL, how does the speed of the ball depend on its depth inside the liquid? Neglect all frictional and other dissipative forces. Assume the depth of the liquid to be large.
The correct Answer is:A, B, C, D
In elastic collision with the surface, direction of velicity is reversed but its magnitude remains the same,
Therefore, time of fall=time of rise,
or, time of fall =t12
Hence, velocity of the ball just before it collides with liquids is
v=g(t1)2
Retardation inside the liquid
a=upthrust-weightmass=VdLg−VdgVd
=(dL−dd)g
Time taken to come to rest under this retardation will be
t=va=gt12a=gt12(dL−dd)g
=dt12(dL−d)
Same will be the time to come to back on the liquid surface.
therefore,
(a) (t2)= time the ball takes to came back to the position from where it was released
=t1+2t=t1+dt1dL−d
=t1[1+ddL−d] or t2=t1dLdL−d
(b) The motion of the ball is periodic but not simple harminic because the acceleration of the ball is g in air and (dL−dd)g inside the liqudi which is not proportional to the displacenent, which is necessary and sufficient condition for SHM.
(c ) When (dL=d), retardation or acceleration inside teh liquid becones zero (upthrust-weight). Therefore, the ball will continue to move with constant velocity v=>12 inside the liquid.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Example 13.1
1 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Example 13.2
1 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based
7 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A ball is dropped from a certain height on a horizontal surface.It bounces up and down,finally comes to rest.If the time taken for first fall is 10s, then find the time taken to come to rest.(e=0.2)
View SolutionThe fraction of a floating object of volume V0and density d0 above the surface of a liquid of density d will be
View Solution
Knowledge Check
A ball of density d is dropped on to a horizontal solid surface. It bounces elastically from the surface and returns to its original position in a time t1 Next, the ball is released and its falls through the same height before striking the surface of a liquid of density dL. Neglect all frictional and other dissipative force. Assume the depth of the liquid to be large.
If d<dL obtain an expression (in terms of d, t1anddL ) for the time t2the ball takes to come back to the position from which it was released.A2t1Bdt1(dL−d)Cdt12(dL−d)D2dt1(dL−d)A ball is dropped from the certain height on the surface of glass. It is collide elastically the comes back to initial position. If this process it repeated then velocity time graph is:-
A B
B C
C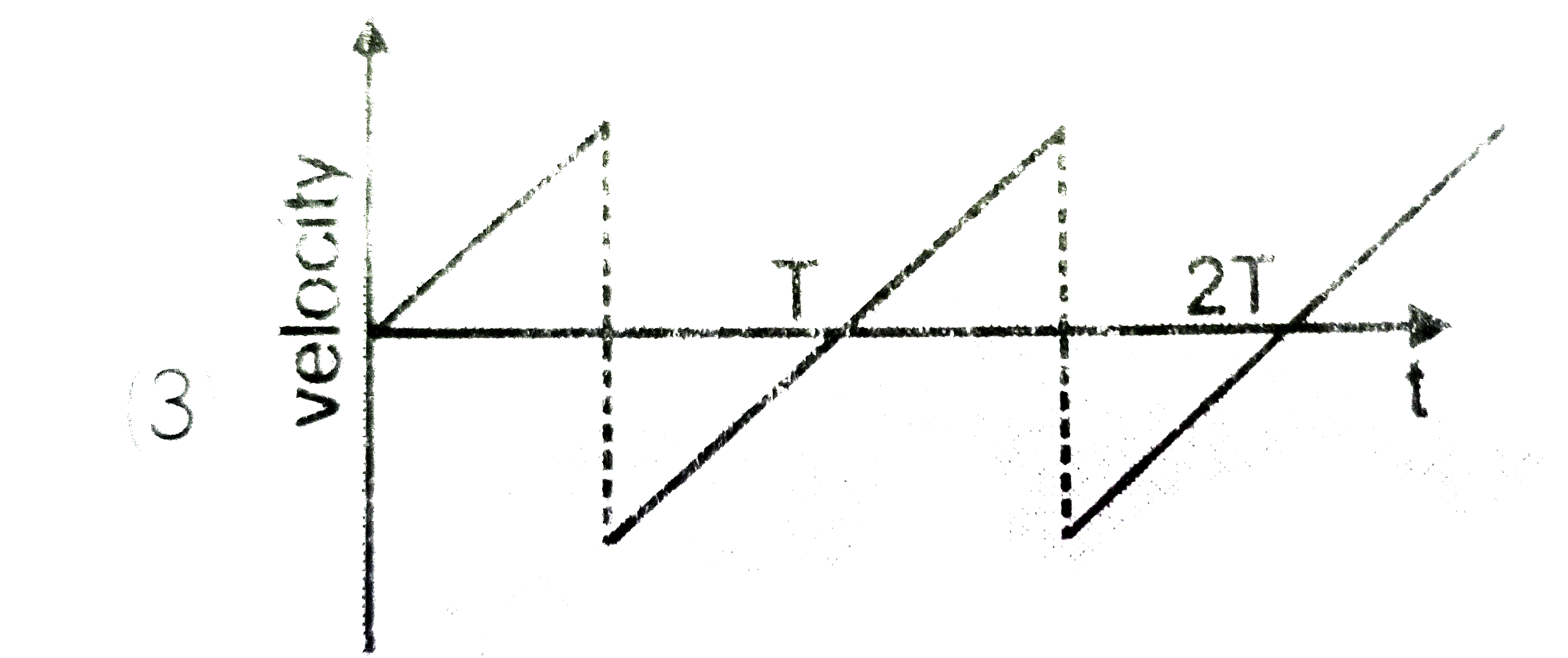 D
D
The fraction of a floating object of volume V0and density d0 above the surface of a liquid of density d will be
Ad0dBdd0d+d0Cd−d0cDdd0d.d0
A ball is dropped on a horizontal surface from height h. If it rebounds upto h2 after first collision then coefficient of restitution between ball and surface is
View SolutionA small ball is dropped from a certain height on the surface of a non-viscous liquid of density less than the density of ball. The motion of the ball is
View SolutionThe height from the surface of earth and electron density of D layer of earth's atmosphere are
View SolutionA ball is dropped on a horizontal surface from height h. If it rebounds upto height h2 after first collision then coefficient of restitution between ball and surface is
View SolutionThe fraction of a floating object of volume V0 and density d0 above the surface of a liquid of density d will be
View Solution
