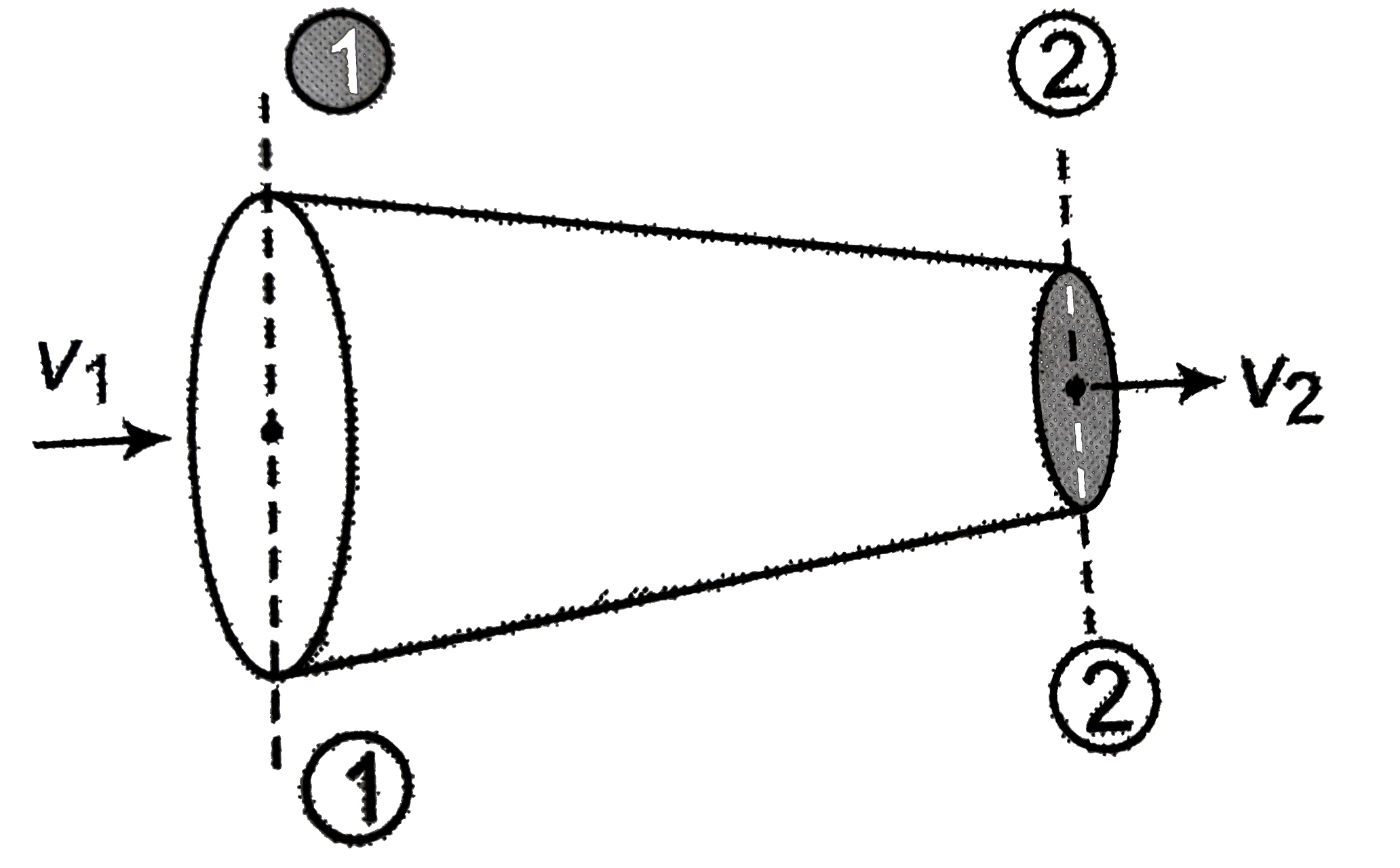
A horizontal pipeline carries water in a streamline flow. At a point along the tube where the cross sectional area is 10−2(m2), the water velcity is 2m/s and the pressure is 8000Pa. The pressure of water at another point where cross sectional area is 0.5×(10)−2(m2) is
4000Pa
1000Pa
2000Pa
3000Pa
The correct Answer is:C
To solve the problem, we will use Bernoulli's equation and the principle of continuity. Here’s a step-by-step solution:
Step 1: Understand the Given Information
We have two points in a horizontal pipeline carrying water:
- Point 1:
- Cross-sectional area A1=10−2m2
- Velocity V1=2m/s
- Pressure P1=8000Pa
- Point 2:
- Cross-sectional area A2=0.5×10−2m2
- Velocity V2=?
- Pressure P2=?
Step 2: Apply the Continuity Equation
According to the continuity equation, the product of the cross-sectional area and velocity at two points in a streamline flow is constant:
A1V1=A2V2
Substituting the known values:
10−2×2=0.5×10−2×V2
This simplifies to:
0.02=0.005×V2
Now, solve for V2:
V2=0.020.005=4m/s
Step 3: Apply Bernoulli's Equation
Bernoulli's equation states:
P1+12ρV21+ρgH1=P2+12ρV22+ρgH2
Since the pipeline is horizontal, H1=H2 and the terms ρgH1 and ρgH2 cancel out. Thus, we can simplify the equation to:
P1+12ρV21=P2+12ρV22
Rearranging gives:
P2=P1+12ρV21−12ρV22
Step 4: Substitute Known Values
Assuming the density of water ρ=1000kg/m3:
P2=8000+12×1000×(22)−12×1000×(42)
Calculating the kinetic energy terms:
P2=8000+12×1000×4−12×1000×16
P2=8000+2000−8000
P2=2000Pa
Final Answer
The pressure of water at the second point is P2=2000Pa.
---
We have two points in a horizontal pipeline carrying water:
- Point 1:
- Cross-sectional area A1=10−2m2
- Velocity V1=2m/s
- Pressure P1=8000Pa
- Cross-sectional area A2=0.5×10−2m2
- Velocity V2=?
- Pressure P2=?
According to the continuity equation, the product of the cross-sectional area and velocity at two points in a streamline flow is constant:
A1V1=A2V2
Substituting the known values:
10−2×2=0.5×10−2×V2
This simplifies to:
0.02=0.005×V2
Now, solve for V2:
V2=0.020.005=4m/s
Bernoulli's equation states:
P1+12ρV21+ρgH1=P2+12ρV22+ρgH2
Since the pipeline is horizontal, H1=H2 and the terms ρgH1 and ρgH2 cancel out. Thus, we can simplify the equation to:
P1+12ρV21=P2+12ρV22
Rearranging gives:
P2=P1+12ρV21−12ρV22
Assuming the density of water ρ=1000kg/m3:
P2=8000+12×1000×(22)−12×1000×(42)
Calculating the kinetic energy terms:
P2=8000+12×1000×4−12×1000×16
P2=8000+2000−8000
P2=2000Pa
The pressure of water at the second point is P2=2000Pa.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Subjective
36 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Assertion and Reason
1 Video
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A horizontal pipelline carries water in a streamline flow . At a point along the pipe , where the cross - sectional area is 10cm2 , the water velocity is 1 m/s and pressure is 2000 Pa . The pressure of water at another point where cross - sectional area is 5cm2 , is _______ (in Pa)
View SolutionA horizontal pipeline carries water in a streamline flow. At a point along the pipe, where the cross- sectional area is 10cm2, the water velocity is 1ms−1 and the pressure is 2000 Pa. The pressure of water at another point where the cross-sectional area is 5cm2, is........Pa. (Density of water =103kg.m−3)
View Solution
Knowledge Check
A long cylindrical tank of radius 1m is being filled by a pipe of radius 2cm. The incoming water has a velocity of 1m/s and pressure is 2000Pa. The pressure of water at another point where the cross-sectional area is 5cm2 is
A0.4mB0.6mC0.8mDthe level will continue to increaseWater is flowing steadily through a horizontal pipe of non - uniform cross - section . If the velocity of water cross - section is 0.02m2 is 2m/s , what is the velocity of water at another point where the cross - section is 0.01m2 ?
A1 m/sB2 m/sC3 m/sD4 m/sA horizontal pipe of non uniform cross section has water flow through it such that the velocity is 2ms−1 at a point where the pressure 40 kpa. The pressure at a point where the velocity of water flow is 3ms−1 is (in kilopascal)
A27B60C37.5D40
Water flowing steadily through a horizontal pipe of non-unifrom cross-section. If the pressure of water is 4×104N/m2 at a point where cross-section is 0.02m2 and velocity of flow is 2ms−1 . The pressure at a point where cross-section reduces to 0.01m2 is 3.4×10n Pa. What is the value of n ?
View SolutionWater is flowing with a speed of 2m/s in a horizontal pipe with cross-sectional area decreasing from 2×10−2m2 to 0.01m2 at pressure 4×104 pascal. What will be the pressure at smaller cross-section?
View SolutionWater is flowing steadily through a horizontal pipe of non-uniform cross-section. If the pressure of water is 4×104N/m2 at a point where cross-section is 0.02m2 and velocity of flow is 2m/s. What is the pressure at a point where cross-section reduces to 0.01m2 ?
 .
.
View SolutionWater from a tap emerges vertically downwards an intial speed of 1 m/s . The cross-sectional area of the tap is 10−4m2 . Assume that the pressure is contant throughout the stream of water and that the flow is steady . The cross-sectional area of the steam. 0.15 m below the tap is
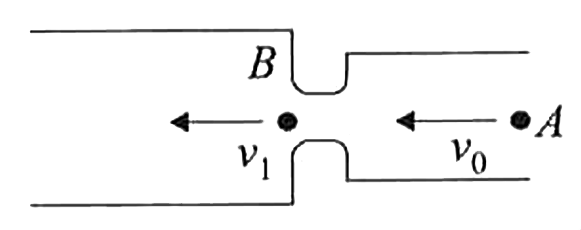
View SolutionThe velocity of an electron at point A1 is V0 where cross sectional area is A. The velocity of electron at the end of contraction at point B, where cross sectional area is 2A, is V1. Find the correct option:
View Solution