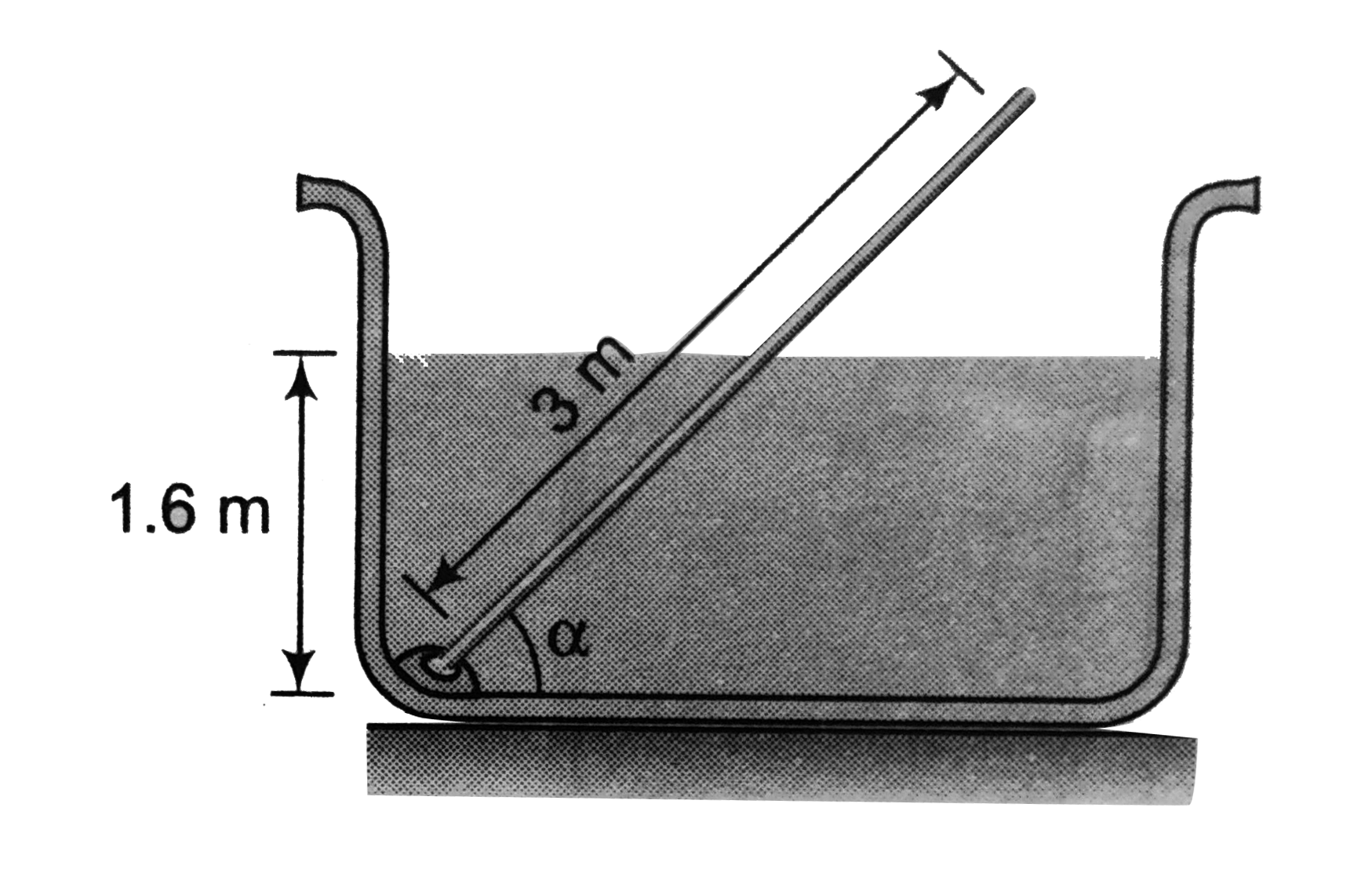
A wooden rod weighing 25N is mounted on a hinge below the free surface of water as shown. The rod is 3m long and uniform in cross section and the support is 1.6m below the free surface. At what angle α rod is in equilibrium? The cross-section of the rod is 9.5×10−4m2 in area. Density of water is 1000kg/m3. Assume buoyancy to act at centre of immersion. g=9.8m/s2. Also find reaction on the hinge in this position.
 .
.
The correct Answer is:A, C, D
Let G be the mid-point of AB and E the mid point of AC(i.e. the centre of buoyancy)

AC=1.6cosecα
Volume of AC
(1.6×9.5×10−4)cosec(α)
Weight of water displaced by AC
=(1.6×9.5×10−4)cosecα
=14.896cosecα
Hence, the buoyant force is 14.896cosedα vertically upwards atE. While the weight of the rod is 25N acting vertically downwards at G. Taking moments about A.
(14.896cosecα)(AEcosα)=(25)(AGcosα)
or, (14.896cosecα)(1.6cosecα2)=25×32
or, sin2α=0.32
∴sinα=0.56
or. α=34.3∘
Further. LetF be the reaction at hinge in vertically downward direction. Then, considering the tranlatory equilibrium of in vertical direction we have,
F+weight of the rod=upthrust
F=upthrust -weight of the rod
=14.896cosec(34.3∘)−25
=26.6−25
∴F=1.6N.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.1
6 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Introductory Exercise
1 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
21 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
For a steel rod, the Young's modulus of elasticity is 2.9×1011N/m2, and the density of steel is 8×103kg/m3.What is the velocity of longitudinal waves in steel?
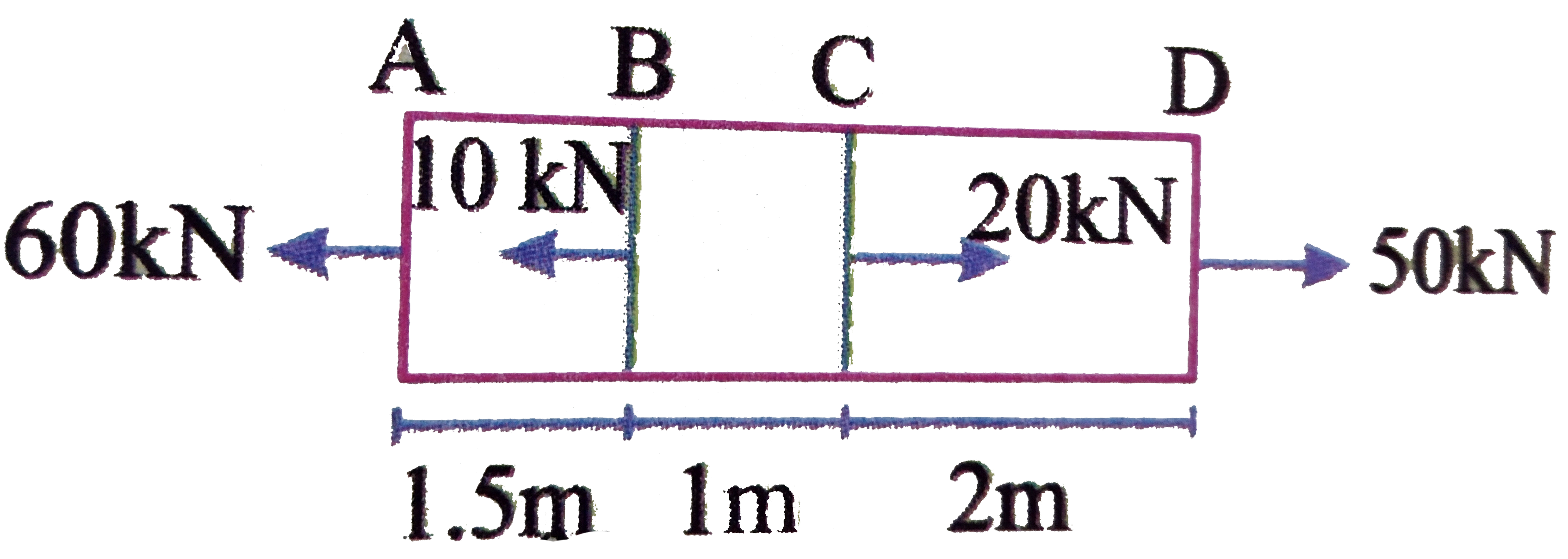
View SolutionA steel rod of cross-sectional area Im2 is acted upon by forces as shown in the Fig. Determine the total elongation of the bar. Take Y=2.0×1011N/m2
View Solution
Knowledge Check
If the young's modulus of the material of the rod is 2×1011N/m2 and its density is 8000kg/m3 then the time taken by a sound wave to traverse 1m of the rod will be
A10−4sB2×10−4sC10−2sD2×10−2sFind the change in density of water in occean at depth of 700m below the surface. The denity of water at the surface is 1000kg/m3 and the bulk modulus of water is 4.9×109Nm−2
A2.4kg/m3B3.4kg/m3C1.4kg/m3D4.4kg/m3A uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :A7F2L6AYB11F2L6AYC5F2L6AYD3F2L2AY
At the mount of the tap area of cross-section is 2.0cm2 and the speed of water is 3m/s. The area of cross-section of the water column 80 cm below the tap is (use g=10m/s2)
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Ratio of elongation in section PQ of rod and section QR of rod is
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Ratio of elastic potential energy stored in section PQ and section QR of the rod is
View SolutionA wooden rod of a uniform cross section and of length 120cm is hinged at the bottom of the tank which is filled with water to a height of 40cm. In the equilibrium position, the rod makes an angle of 60∘ with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of
View SolutionA metal rod of length 2.5m and area of cross-section 2.5×10−4m2 is elongated by 2.5×10−3m by a force of 600N. Then energy stored in the rod is,
View Solution
