The density inside a solid sphere of radius a is given by , where is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
The correct Answer is:A, B
Volume of small strip mass of this strip
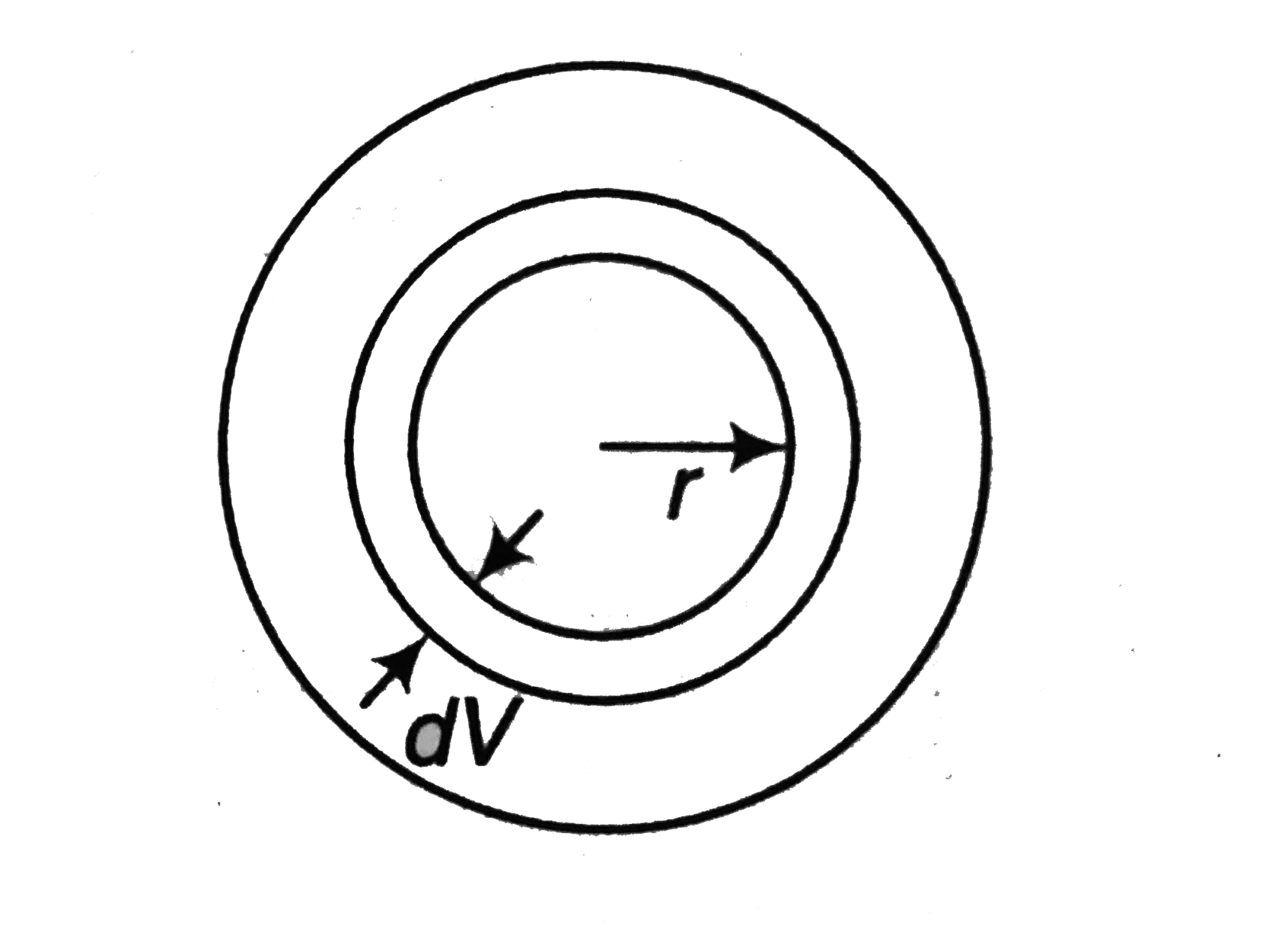
Mass of whole sphare
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Level 2 Single Correct
Explore 22 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Level 2 More Than One Correct
Explore 10 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Level 1 Single Correct
Explore 27 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 11 Videos
Similar Questions
The density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0(1−ra), where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View Solution
Knowledge Check
A non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
AIncreases as r increases inside the sphereBDecreases as r increases inside as well as outsideCIncreases as increases outside the sphereDIs discontinuousat r=RA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
Adecreases as r increases for r<R and r>RBincreases as r increases for r<R and r>RCzero as r increases for r<R, decreases as r increases for r>RDzero as r increases for r<R, increases for r>RInside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
AE=−23πGρlBE=−43πGρlCE=−43π2GρlDE=−43πGρ2l2
The volume charge density inside of sphere of radius R is given by ρ=ρ0(1−rR) ,where ρ0 is constant and r distance from centre.
(a) Find total charge Q inside sphere.
Electric field outside sphere at distance r from centre.
(b) Electric field outside sphere at distance r from centre.
(c) Electric field inside sphere at distance r from centre.
(d) At what distance from centre electric field is maximum and its value?
(e ) Sketch E versus r graph.
View SolutionA solid sphere of radius R has a mass distributed in its volume of mass density ρ=ρ0 r, where ρ0 is constant and r is distance from centre. Then moment of inertia about its diameter is
View SolutionInside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength G of the gravitational field inside the cavity.
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionThere is one long non-conducting solid cylinder of radius R. The volume charge density is given by ρ=kx2 where k is a constant and x is the distance of the point from centre of cylinder. Electric field intensity inside the cylinder at a distance x from the centre is
View Solution

