Three points A , B and C each of mass are placed in a line with AB=BC=d. Find the gravitational force on a fourth particle P of same mass placed at a distance d from the particle B on the perpendicular bisector of the line AC.
The correct Answer is:A, B, D
Fnet=2(F1cos45∘)+F2
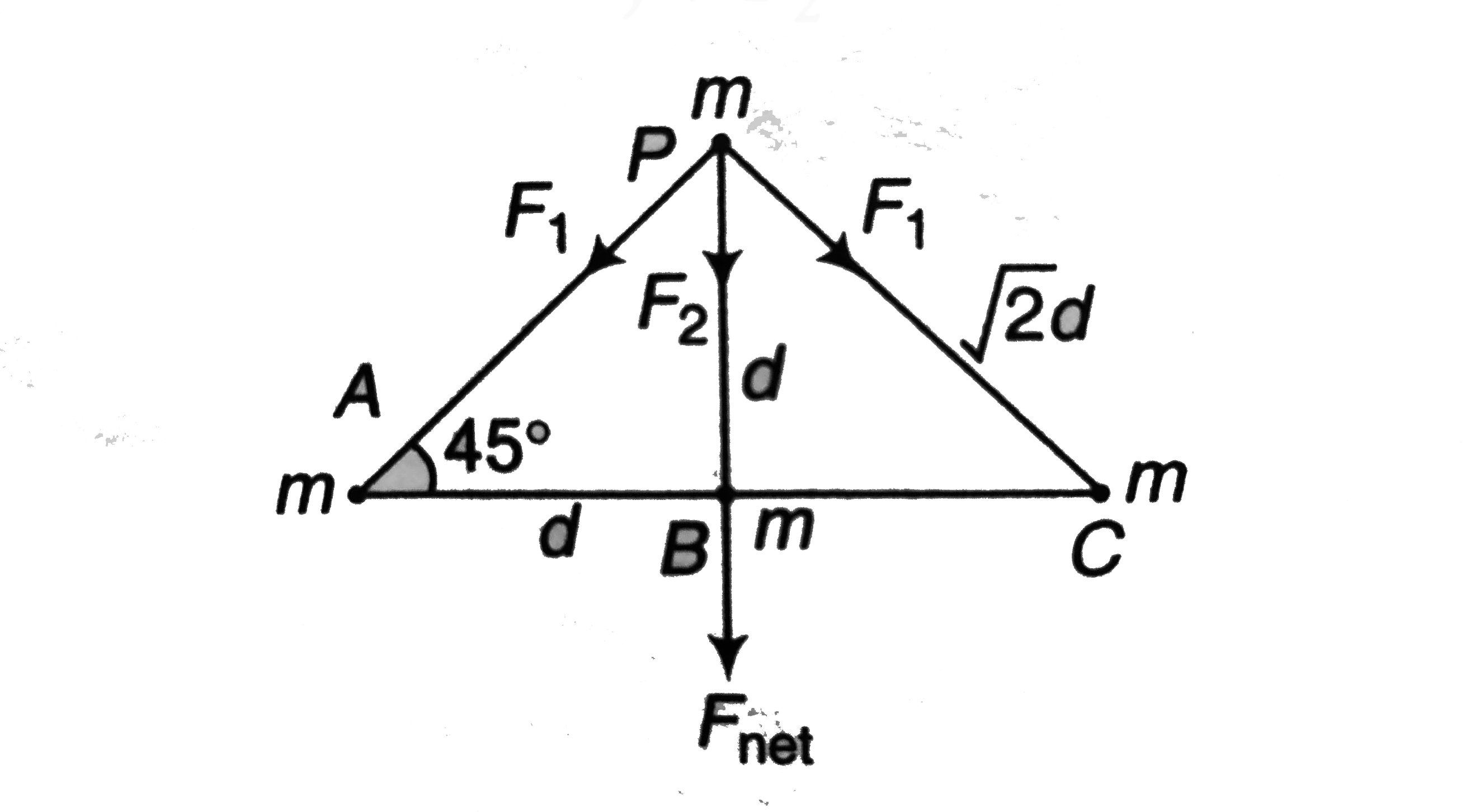
=√2F1+F2=(√2)Gmm(√2d)2+Gmmd2
=(√2+1√2)Gm2d2 (Along PB)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Exercise 13.29videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Exercise 13.35videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples8videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE11videos
KINEMATICS
Similar Questions
Three portion A , B and C each of mass re placed ina line with AB=BC=d. Find the gravittional force on a fourth article P of same mass placed at a distance d from the particle B on the perpendicular bisector of the line AC.
View SolutionA tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View Solution
Knowledge Check
- Question 1 - Select One
Two particles each of mass 'm' are placed at A and C are such AB=BC=L. The gravitational force on the third particle placed at D at a distance L on the perpendicular bisector of the line AC is
AGm2L2 along BDBGm2√2L2 along DBCGm2L2 along ACDGm2√2L2 along BD - Question 2 - Select One
Three equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .AGm2a2B4Gm23a2C3Gm2a2Dzero - Question 3 - Select One
Three equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .AGm2a2B4Gm23a2C3Gm2a2Dzero
Four particles having masses, m, wm, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View SolutionAssume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless.
(a) Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel.
(b) Find the component of this force along the tunnel and perpendicular to the tunnel.
(c) Find the normal force exerted by the wall on the particle.
(d) Find the resultant force on the particles.
(e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the
(a) the mid point of a side
(b) centre of the triangleView Solution

