Three balls A, B and C are placed on a smooth horizontal surface. Given that mA=mC=4mB. Ball B collides with ball C with an initial velocity v as shown in figure. Find the total number of collisions between the balls. All collisions are elastic.
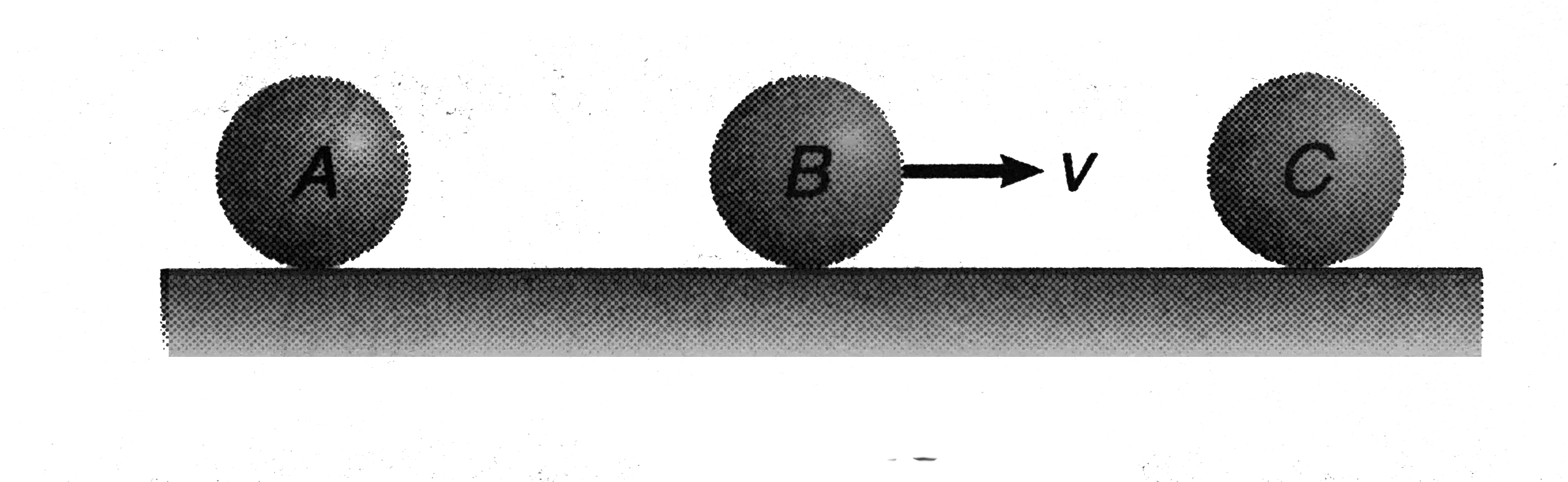
After first collision with B+C

vB'=(m−4mm+4m)v=−35v
vC'=(2×mm+4m)v=25v
After second collision with B+A

Now since 925v<25v or vC
So, B will not collide with C further,
Hence total collisions are only 2.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Assertion and Reason
Explore 15 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Objective
Explore 42 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Exercise 11.5
Explore 4 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEYChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
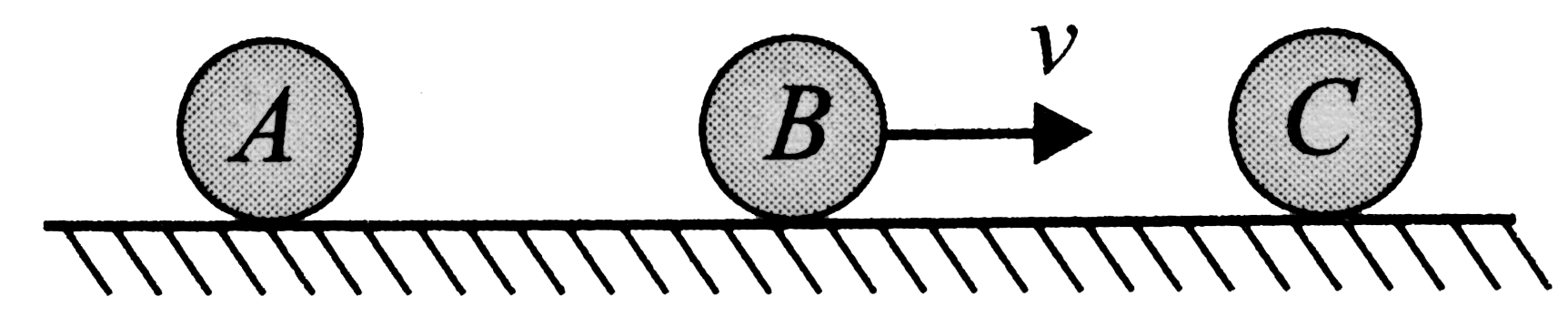
Three balls A,B and C(mA=mC=4mB) are placed onn a smooth horizontal surface. Ball B collides with ball C with an initial velocity v as shown in figure. Find the total number of collision betwenent the balls (all collisions are elastic).
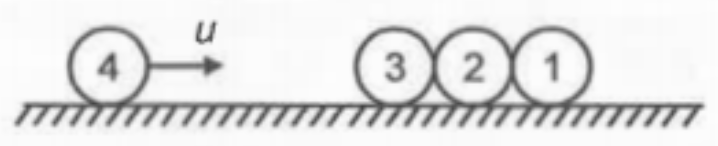
View SolutionThree identical balls 1, 2 and 3 are placed together at rest on a smooth horizontal surface. A fourth identical ball moving with velocity u in line of first three balls collides head on elastically as shown in figure, then
View Solution
Knowledge Check
A ball A of mass M collides elastically with a similar ball B at rest as shown in figure. Initially velocity of ball A is u m/s. After collision,
 ASpeed of ball B is u sinθBVelocity of ball A is usin2θˆi+usinθcosθˆjCSpeed of ball A is ucosθDVelocityofballBisu cos theta sin theta hati + u cos^2 theta hatj
ASpeed of ball B is u sinθBVelocity of ball A is usin2θˆi+usinθcosθˆjCSpeed of ball A is ucosθDVelocityofballBisu cos theta sin theta hati + u cos^2 theta hatjTwo balls marked 1 and 2 of the same mass m and a third ball marked 3 of mass M are arranged over a smooth horizontal surface as shown in the figure. Ball 1 moves with a velocity v1 towards ball 2. All collisions are assumed to be elastic. If M<m, the number of collisions between the balls will be.
 A1B2C3D4
A1B2C3D4N identical balls are placed on a smooth horizontal surface. An another ball of same mass collides elastically with velocity u with first ball of N balls. A process of collision is thus started in which first ball collides with second ball and the with the third ball and so on. The coefficient of restitution for each collision is e. Find the speed of Nth ball.
A(1+e)NuBu(1+e)N−1Cu(1+e)N−12N−1DuN(1+e)N
Three balls A,B and C of same mass m are placed on a frictionless horizontal plane in a straight line as shown. Ball A is moved with velocity u towards the middle ball B. If all the collisions are elastic, find the final velocities of all the balls.

View SolutionA ball moving with speed v collides with a horizontal smooth surface at an angle θ with normal to surface as shown in figure. If coefficient of restitution of collision is e, then find v'

View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View SolutionA ball A of mass 3m is placed at a distance d from the wall on a smooth horizontal surface Another ball B of mass m moving with velocity u collides with ball A. The coefficient of restitution between the balls and the wall and between the balls is e
(a) the velocity of ball B after collision is u(3e−1)4.
(b) the velocity of ball B after collision is u(2e−1)4.
( c) after collision, ball A will have away by distance d(2e−1)(2e−1) during the time ball B returns back to wall.
(d) after collision, ball A will move away by distance d(e−1)(3e−1) during the time ball B returns back to wall.
View Solution

