Two particles of masses 1kg and 2kg respectively are initially 10m aprt. At time t=0, they start moving towards each other with uniform speeds 2m/s and 1m/s respectively. Find the displacement of their centre of mass at t=1s.
SCM=m1S1+m2S2m1+m2
=m1(v1t)+m2(v2t)m1+m2
=(1)(2)(1)+(2)(−1)(1)1+2
=0
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.3
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.4
4 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.1
13 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Two men to masses 80kg and 60kg are standing on a wood plank of mass 100kg, that has been placed over a smooth surface. If both the men start moving towards each other with speeds 1m/s and 2m/s respectively then find the velocity of the plank by which it starts moving.
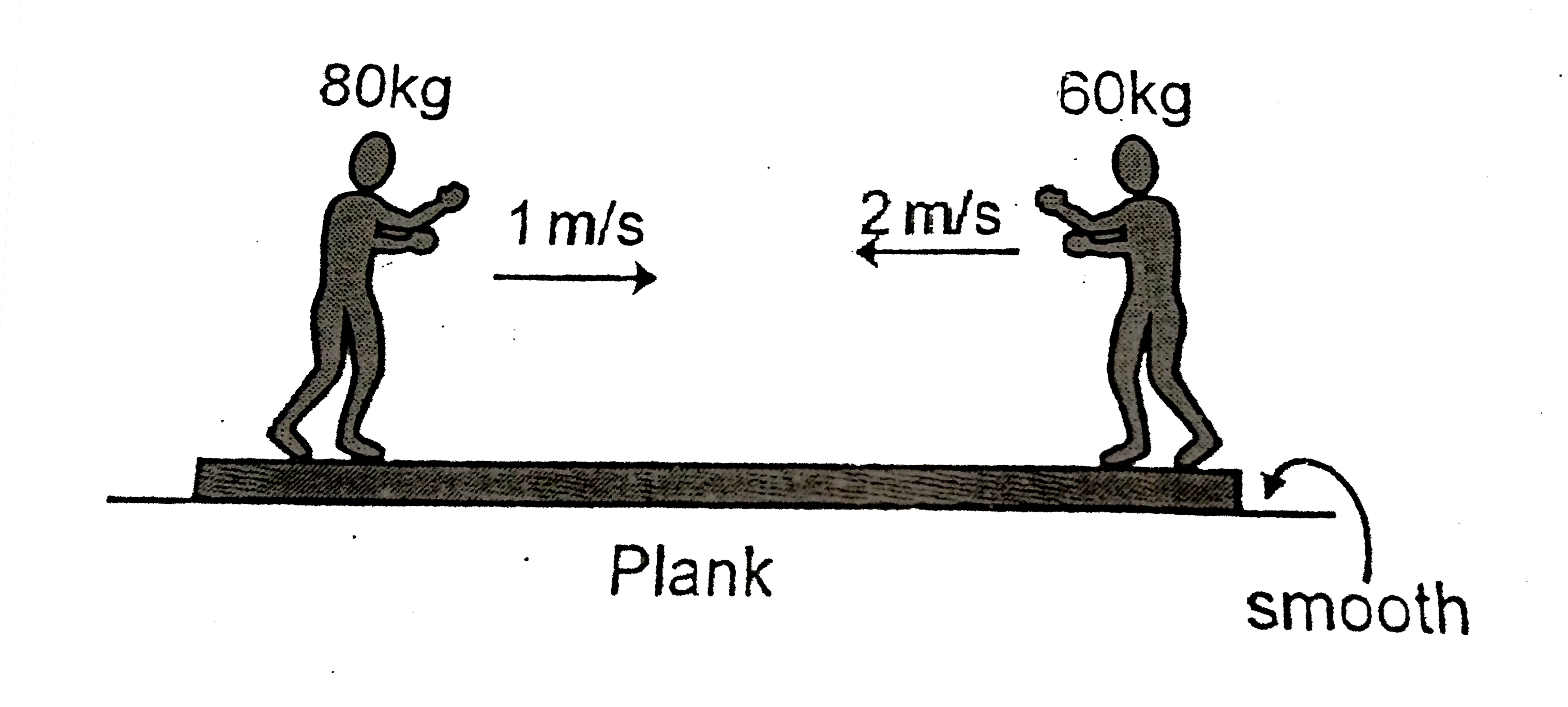
View SolutionTwo particles of masses 2kg and 4kg are approaching towards each other with accelerations 1m/s2 and 2m/s2, respectively, on a smooth horizontal surface. Then find the acceleration of centre of mass of the system and direction of acceleration of CM.
View Solution
Knowledge Check
Two particles of masses 2kg and 3kg are projected horizontally in opposite directions from the top of a tower of height 39.2m with velocities 5m/s and 10m/s respectively. The horizontal range of the centre of mass of two particles is
A8√2m in the direction of 2kgB8√2m in the direction of 3kgC√8m in the direction of 2kgD√8m in the direction of 3kgTwo particles A and B masses 1 kg and 2 kg respectivelty are projected in the same vertical line as shown in figure with speeds uA=200m/s and uB=85m/s respectively. Initially they were 90 m apart. Find the maximum height attained by the centre of mass of the system of particles A and B, from the initial position of centre of mass of the system. Assume that none of these particles collides with the ground in that duration Take g=10m/s2
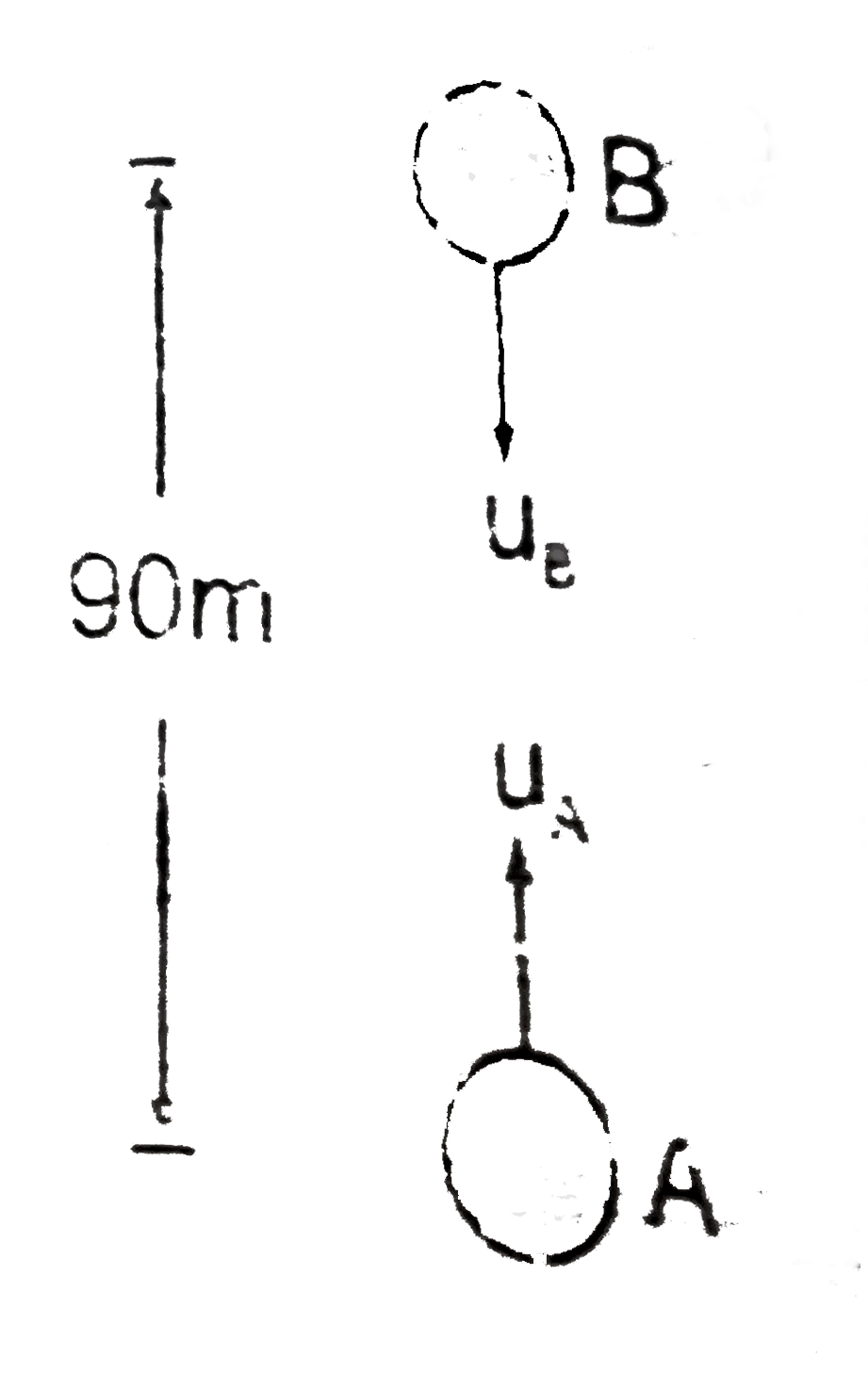 A5 meterB10 meterC25 meterD20 meter
A5 meterB10 meterC25 meterD20 meterTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
A103m/sB107m/sC112m/sD123m/s
Two men of masses 80kg and 60kg are standing on a wooden plank of mass 100kg, that has been placed over a smooth surface. If both the men start moving toward each other with speeds 1ms and 2ms, respectively, then the magnitude of velocity of the plank by which it starts moving is ∣∣∣pq∣∣∣ms. Find (p+q).
'(##CEN_KSR_PHY_JEE_C08_E01_010_Q06##)'
View SolutionTwo particles A and B of equal size but of masses m kg and 2 m kg are moving directly towards each other with speeds 21 m/s and 4 m/s respectively. After collision, A moves with a speed of 1 m/s in the original direction. Then:
View SolutionTwo particle of mass 2kgand1kg are moving along the same straight line with speeds 2m/sand5m/s respectively. What is the speed of the centre of mass of the system if both the particles are moving (a) in same direction (b) in opposite direction ?
View SolutionTwo bodies of masses 2 kg and 4 kg are moving with velocities 2 m/s and 10 m/s respectively along same direction. Then the velocity of their centre of mass will be
View SolutionTwo bodies of masses 0.1 kg and 0.4 kg move towards each other with the velocities 1 m/s and 0.1 m/s respectively, After collision they stick together. In 10 sec the combined mass travels
View Solution
