If a point moves along a circle with constant speed, prove that its angular speed about any point on the circle is half of that about the centre.

A

$2 ω_{c} = ω_{0}$

B

$ω_{c} = ω_{0}$

C

$ω_{c} = 2 ω_{0}$

D

$ω_{c} = (\frac{1}{2}) ω_{0}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let, $O$ be a point on a circle and $P$ be the position of the particle at any time $T$ , such that
$∠ P O A = θ$ . Then, $∠ P C A = 20$
Here, $C$ is the centre of the circle.
Angular velocity of $P$ about $O$ is $ω_{0} = \frac{d θ}{d t}$
and angular velocity of $P$ about $C$ is,
$ω_{c} = \frac{d}{d t} (2 θ) = 2 \frac{d θ}{d t}$
or $ω_{c} = 2 ω_{0}$

|

Updated on:21/07/2023

Class 11 PHYSICS CIRCULAR MOTION

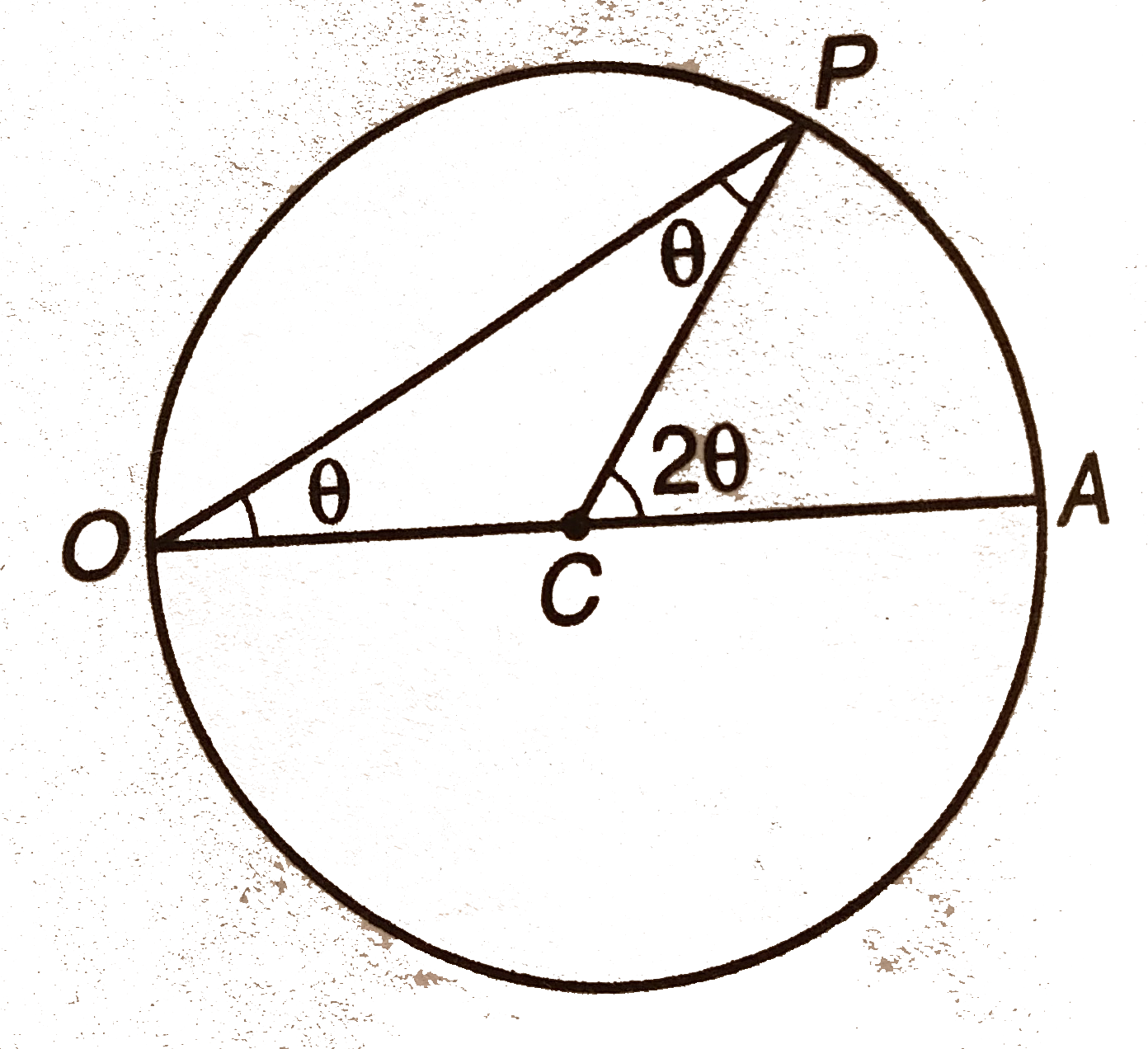
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the body is moving in a circle of radius r with a constant speed v , its angular velocity is
A $v^{2} / r$
Bvr
Cv/r
Dr/v
Question 2 - Select One
Assertion : A body is moving along a circle with a constant speed. Its angular momentum about the centre of the circle remains constant
Reason : In this situation, a constant non-zero torque acts on the body.
AIf both Assertion and Reason are correct and Reason is the correct explanation of Assertion
BIf both Assertion and Reason are true but Reason is not the correct explanation of Assertion
CIf Assertion is true but Reason is fasle
DIf Assertion is false but Reason is true
Question 3 - Select One
A particle is moving in a circle with a constant speed. Its moving is
APeriodic
BOscillatory
CSimple harmonic
Dboth 'a' and 'b'

DC PANDEY-CIRCULAR MOTION-Miscellaneous Examples

Home
Ask Doubt
Profile