A turn of radius 20m is banked for the vehicle of mass 200kg going at a speed of 10m/s. Find the direction and magnitude of frictional force (a) 5m/s
(b) 15m/s
Assume that friction is sufficient to prevent slipping. (g=10m/s2)
f=200√5N (down wards)
f=500√5N (up wards)
f=500√5N (down wards)
f=200√5N (up wards)
The correct Answer is:C
To solve the problem of finding the direction and magnitude of the frictional force acting on a vehicle of mass 200 kg moving around a banked turn of radius 20 m at different speeds (5 m/s and 15 m/s), we will follow these steps:
Step 1: Calculate the banking angle (θ)
The banking angle can be calculated using the formula:
tanθ=v2rg
Where:
- v=10m/s (the speed of the vehicle)
- r=20m (the radius of the turn)
- g=10m/s2 (acceleration due to gravity)
Substituting the values:
tanθ=(10)220×10=100200=0.5
Now, calculating θ:
θ=tan−1(0.5)≈26.56∘
Step 2: Analyze the forces acting on the vehicle at 5 m/s
When the vehicle is moving at a speed less than 10 m/s, the frictional force will act towards the center of the circular path to prevent slipping outward.
- Forces in the horizontal direction (centripetal force):
Nsinθ−Fcosθ=mv2r
- Forces in the vertical direction:
Ncosθ+Fsinθ=mg
Step 3: Substitute known values for 5 m/s
1. Calculate the centripetal force:
mv2r=200×(5)220=200×2520=250N
2. Set up the equations:
- Horizontal:
Nsin(26.56∘)−Fcos(26.56∘)=250
- Vertical:
Ncos(26.56∘)+Fsin(26.56∘)=2000N(since mg=200×10)
Step 4: Solve the equations
Using the trigonometric values:
- sin(26.56∘)≈0.447
- cos(26.56∘)≈0.894
Substituting these values into the equations:
1. 0.894N−0.447F=250 (1)
2. 0.447N+0.894F=2000 (2)
From equation (1):
N=250+0.447F0.894
Substituting N into equation (2):
0.447(250+0.447F0.894)+0.894F=2000
Solving this will yield the value of F (frictional force).
Step 5: Calculate the frictional force
After solving the above equations, we find:
F≈300√5N(upward direction)
Step 6: Analyze the forces acting on the vehicle at 15 m/s
When the vehicle is moving at a speed greater than 10 m/s, the frictional force will act towards the center of the circular path.
1. Calculate the centripetal force for 15 m/s:
mv2r=200×(15)220=200×22520=2250N
2. Set up the equations:
- Horizontal:
Nsin(26.56∘)+Fcos(26.56∘)=2250
- Vertical:
Ncos(26.56∘)−Fsin(26.56∘)=2000
Step 7: Solve the equations for 15 m/s
Using the same trigonometric values as before, we can substitute and solve:
1. 0.894N+0.447F=2250 (1)
2. 0.447N−0.894F=2000 (2)
After solving these equations, we find:
F≈500√5N(downward direction)
Final Answers:
- For speed 5 m/s: Frictional force = 300√5N (upward)
- For speed 15 m/s: Frictional force = 500√5N (downward)
The banking angle can be calculated using the formula:
tanθ=v2rg
Where:
- v=10m/s (the speed of the vehicle)
- r=20m (the radius of the turn)
- g=10m/s2 (acceleration due to gravity)
tanθ=(10)220×10=100200=0.5
Now, calculating θ:
θ=tan−1(0.5)≈26.56∘
When the vehicle is moving at a speed less than 10 m/s, the frictional force will act towards the center of the circular path to prevent slipping outward.
Nsinθ−Fcosθ=mv2r
- Forces in the vertical direction:
Ncosθ+Fsinθ=mg
1. Calculate the centripetal force:
mv2r=200×(5)220=200×2520=250N
- Horizontal:
Nsin(26.56∘)−Fcos(26.56∘)=250
- Vertical:
Ncos(26.56∘)+Fsin(26.56∘)=2000N(since mg=200×10)
Using the trigonometric values:
- sin(26.56∘)≈0.447
- cos(26.56∘)≈0.894
1. 0.894N−0.447F=250 (1)
2. 0.447N+0.894F=2000 (2)
N=250+0.447F0.894
0.447(250+0.447F0.894)+0.894F=2000
Solving this will yield the value of F (frictional force).
After solving the above equations, we find:
F≈300√5N(upward direction)
When the vehicle is moving at a speed greater than 10 m/s, the frictional force will act towards the center of the circular path.
mv2r=200×(15)220=200×22520=2250N
- Horizontal:
Nsin(26.56∘)+Fcos(26.56∘)=2250
- Vertical:
Ncos(26.56∘)−Fsin(26.56∘)=2000
Using the same trigonometric values as before, we can substitute and solve:
1. 0.894N+0.447F=2250 (1)
2. 0.447N−0.894F=2000 (2)
F≈500√5N(downward direction)
- For speed 5 m/s: Frictional force = 300√5N (upward)
- For speed 15 m/s: Frictional force = 500√5N (downward)
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Solved Examples
2 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Miscellaneous Examples
5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A turn of radius 100 m is banked for a speed of 20 m/s
(a) Find the banking angle
(b) If a vehicle of mass 500 kg negotiates the curve find the force of friction on it if its speed is – (i) 30 m/s (ii) 10 m/s
Assume that friction is sufficient to prevent skidding and slipping.
[Take tan22∘=0.4,sin22∘=0.375,cos22∘=0.93,g=10ms−2]
View SolutionA block of mass 2.00 kg moving at a speed of 10.0 m/s accelerates at 3.0 ms2 for 5.00 s. Compute its final kinetic enegy.
View Solution
Knowledge Check
A turn of radius 600 m is banked for a vehicle of mass 200 kg going with a speed of 180kmh−1 . Determine the banking angle of its path.
A22.6∘B19.8∘C30.6∘D40.8∘A body of mass 1 kg falls from rest through a distance of 200 m and acquires a speed of 50 m/s. Work done against friction of air is (Take g=10m/s2)
A700 JB1250 JC750 JD1960 JAn object of mass 2 kg is whirled rround in a verticle circle of radius 1m with a constant speed of 4m/s .Then the maximum tension in the string is (g=10m/s2)
A32 NB52 NC72 ND92 N
An object of mass 200 kg is accelerated uniformly from a velocity of 4ms−1to8ms−1 in 10 s . Find the magnitude of the force exerted on the object
View Solution5A body of mass 15 kg moving with a velocity of 10 m/s is to be stopped by a resistive force in 15 sec, the force will be -
View SolutionThe 10kg block is moving to the left with a speed of 1.2m/s at time t=0 A force F is applied kinetic friction is μk=0.2. Determine the time t at which the block comes to a slip. (g=10m/s2)
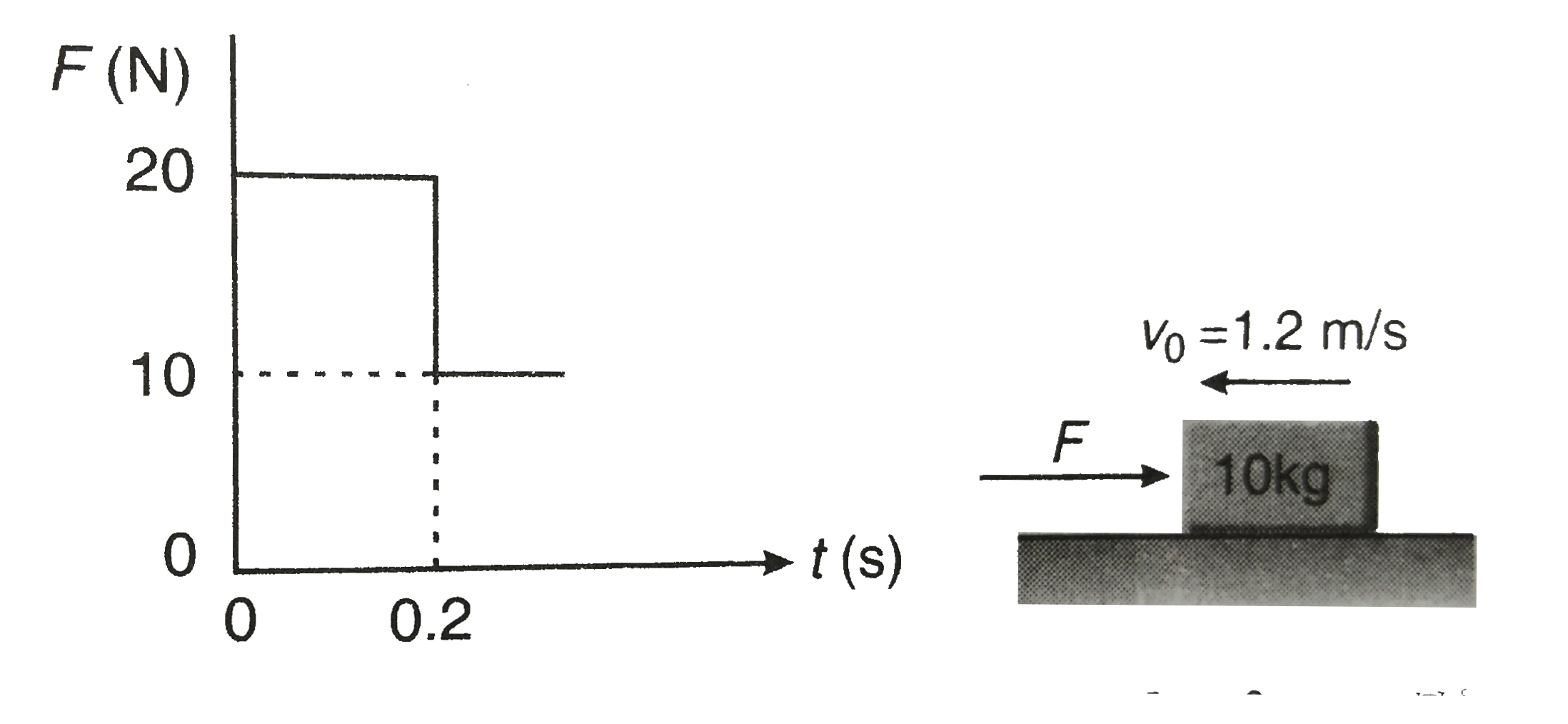
View SolutionA train of mass 105 kg rounds a curve of radius 100m at a speed of 20 m/s . If the track is not , then the thrust on the outer rail of the track is
View SolutionA bullet of mass 10 g is fired with a velocity of 20 m/s from a gun of mass 2 kg. Find the recoil velocity (in m/s) of the gun.
View Solution
