Two identical blocks are placed over a rought inclined plane. One block is given an upward velocity to the block and the other is doenward direction. If μ=13 and θ=45∘ the ratio of magnitudes of acceleration of two is 2:1
The desired ratio is 1+μ1−μ
If both Accertion and Reason are true and the reason is correct explanation of the Assertion.
If both Accertion and Reason are true but reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:A
a1=gsinθ+μgcosθ
a2=gsinθ−μgcosθ
:. a1a2=1+μ1−μ for θ=45∘
Similar Questions
A body of mass M is placed on a rough inclined plane of inclination θ and coefficient of friction μk. A force of (mgsinθ+μkmgcosθ) is applied in the upward direction, the acceleration of the body is
View SolutionFind the ratio of work done by gravity on the block under the two conditions. Assume μ=0 between block and plane.
View Solution
Knowledge Check
A body of mass M is placed on a rough inclined plane of inclination θ and coefficient of friction μk A force of (mgsinθ+μkmgcosθ) is applied in the upward direction the acceleration of the body is .
AgsinθBg(sinθ+μkcosθ)Cg(sinθ+μkcosθ)DZeroA block A slides over another block B which is placed over a smooth inclined plane. The coefficient of friction between the two blocks. A and B is μ. Mass of block B is two times the mass of block A. The acceleration of the centre of mass of two blocks is
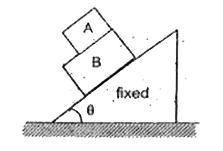AgsinθBgsinθ−μgcosθ3Cgsinθ3D2gsinθ−μgcosθ3A block is kept on an inclined plane of inclination θ of length l. the velocity of particle at the bottom of inclined is (the coefficient of friction is μ)
A√2gl(μcosθ−sinθ)B√2gl(sinθ−μcosθ)C√2gl(sinθ+μcosθ)D√2gl(cosθ+μsinθ)
A cubical block rests on an inclined plance of μ=1√3 . Determine the angle at which the block just slides down the incline .
View SolutionA block of mass 1kg is placed on a rough inclined plane at angle θ=45∘ will horizontal . The block is connected with a straight as straight as shown in figure if μ=3/4 find the tension in string
View SolutionA block of mass m is placed on a rough inclined plane. The coefficient of friction between the block and the plane is μ and the inclination of the plane is θ. Initially theat−0 and the block will certain stationary on the plane. Now the inclination θ is gradually increased. The block presses the inclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the block starts sliding, the angle θ for which the block starts sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction ( frictional force) and the shear reaction (frictional force) . The net contact force will be resultant of both.
If the entire system, were accelerated upward with acceleration 'a', the angle of repose , would :
View Solution
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If μ=34 then what will be frictional force (shear force) acting between the block and inclined plane when θ=30∘:
View SolutionA block of mass m is placed on a rough inclined plane of inclination θ kept on the floor of the lift. The coefficient of friction between the block and the inclined plane is μ. With what acceleration will the block slide down the inclined plane when the lift falls freely ?
View Solution