In the abjoining figure, wire is smooth, ring has a mass and block . If system is released from rest with ,find
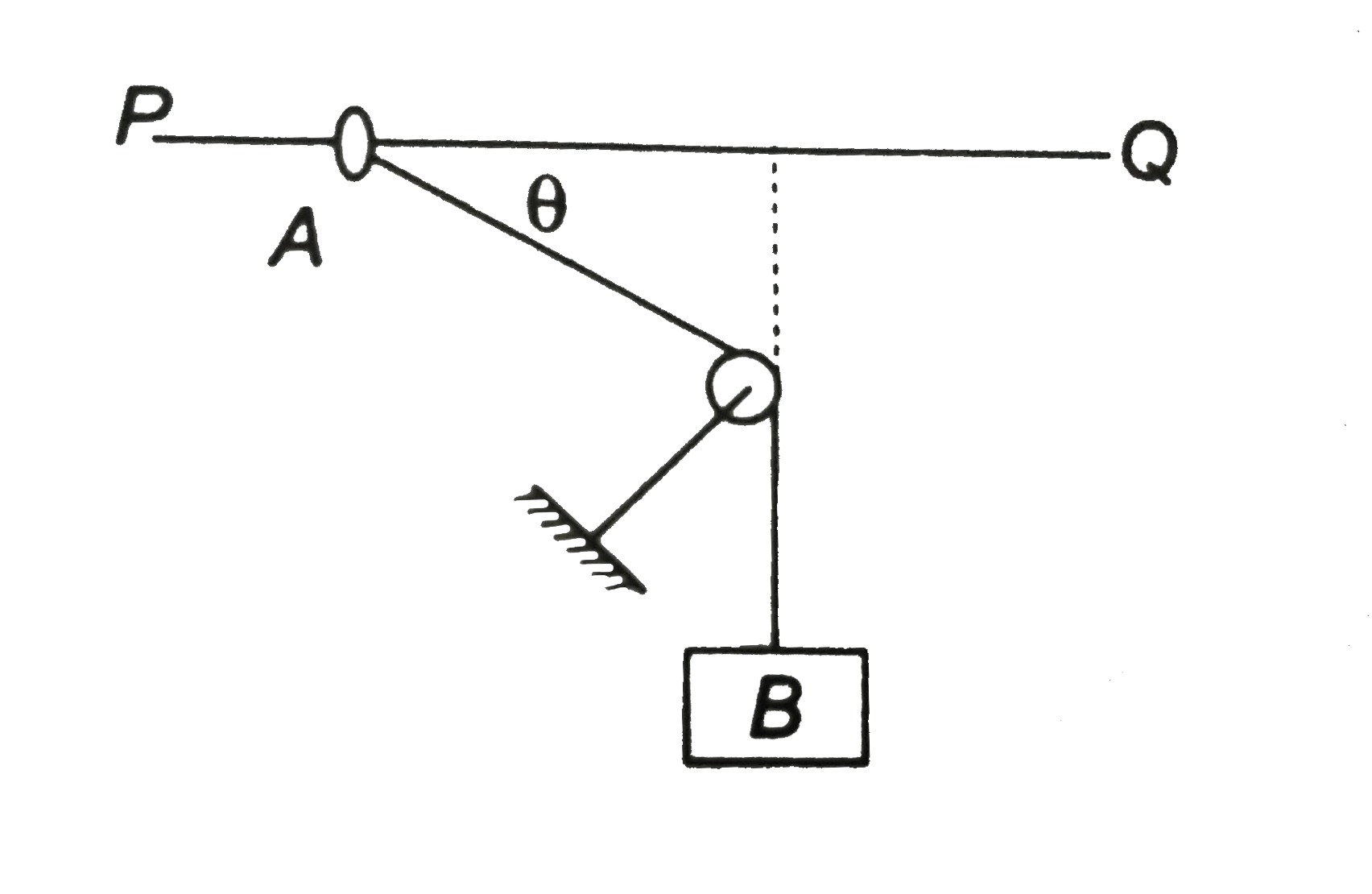
(a)constraint relation between their velocities as a function of .
(b) constrain relation between their accelerations just after the release at .
(c) tension in the string and the value of these accelerations at this instant.
and are two fixed fixed points. Therefore.
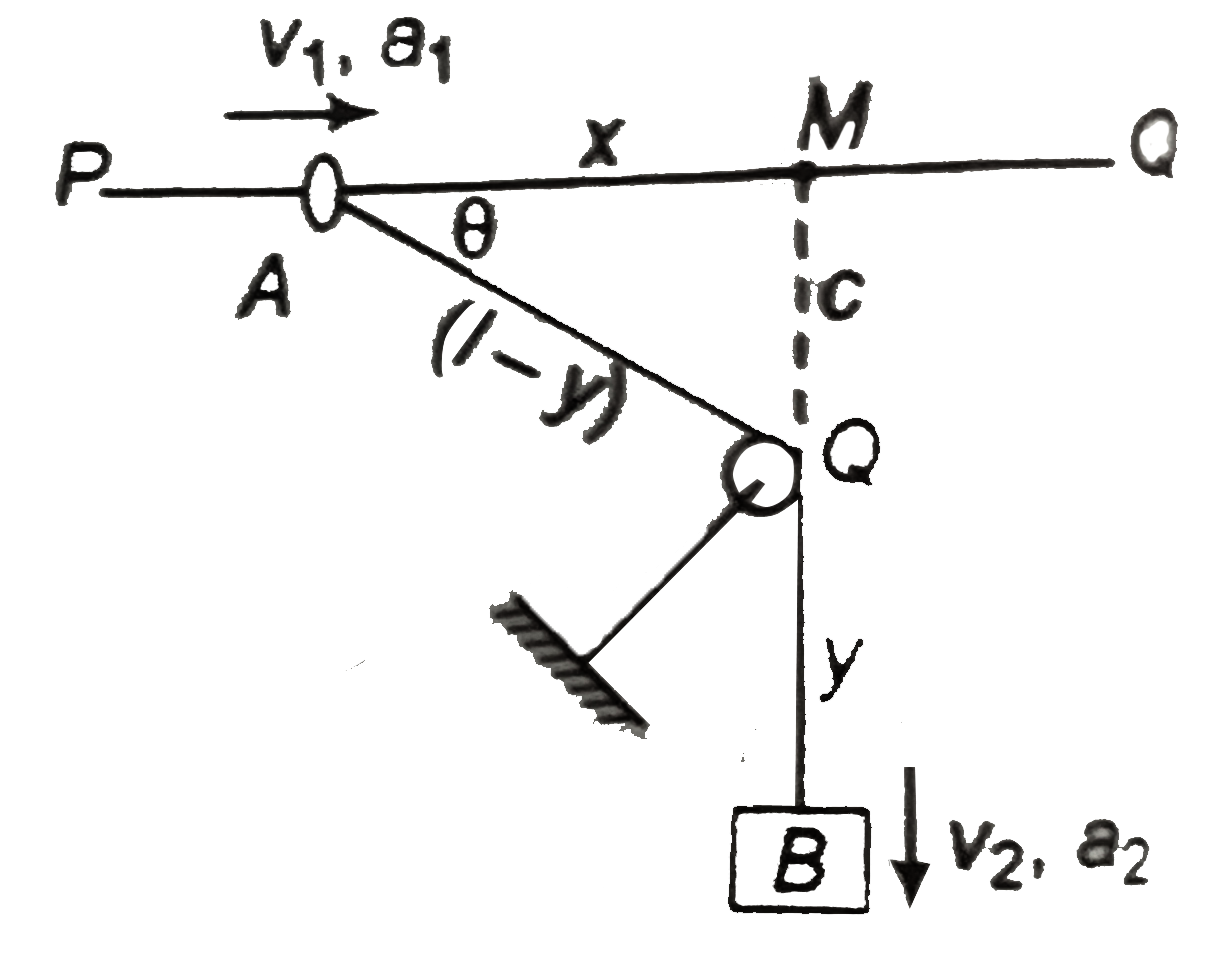 (a) In traingle
(a) In traingle
Differentiating w.r.t time, we get
or ...(i)
...(ii)
y is increasing with time,
x is increasing with time,
and
Substituting these value in Eq (ii) we have
(b) Further differentiating Eq. (i) we have,
...(iii)
Just after the release, and all are zero.Substituting in Eq. (iii), we have ,
...(iv)
Here
Substituting in Eq. (iv), we have ...(v)
(c) For Equation is

or ...(vi)
For
...(vii)
Solving Eqs. and , we get
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Miscellaneous Examples
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.1
10 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
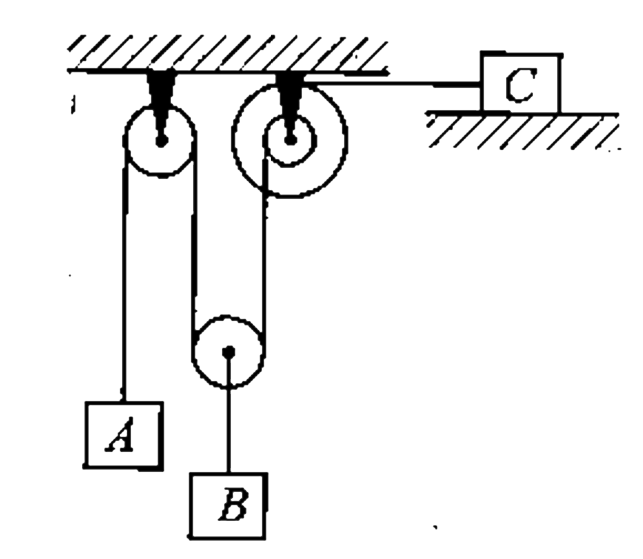
Find the constrained relation among the acceleration of blocks A, B and C for the situation shown in figure-1.97. Ratio of radii of step pulley is given as 1:2.
View SolutionConsider the system shown in fig. the system os released from rest, find the tension in the cord connected between 1kg and 2 kg blocks.

View Solution
Knowledge Check
The blocks A and B shown in figure have masses MA=5kg and MB=4kg. The system is released from rest. The speed of B after A has travelled a distance 1m along the incline is
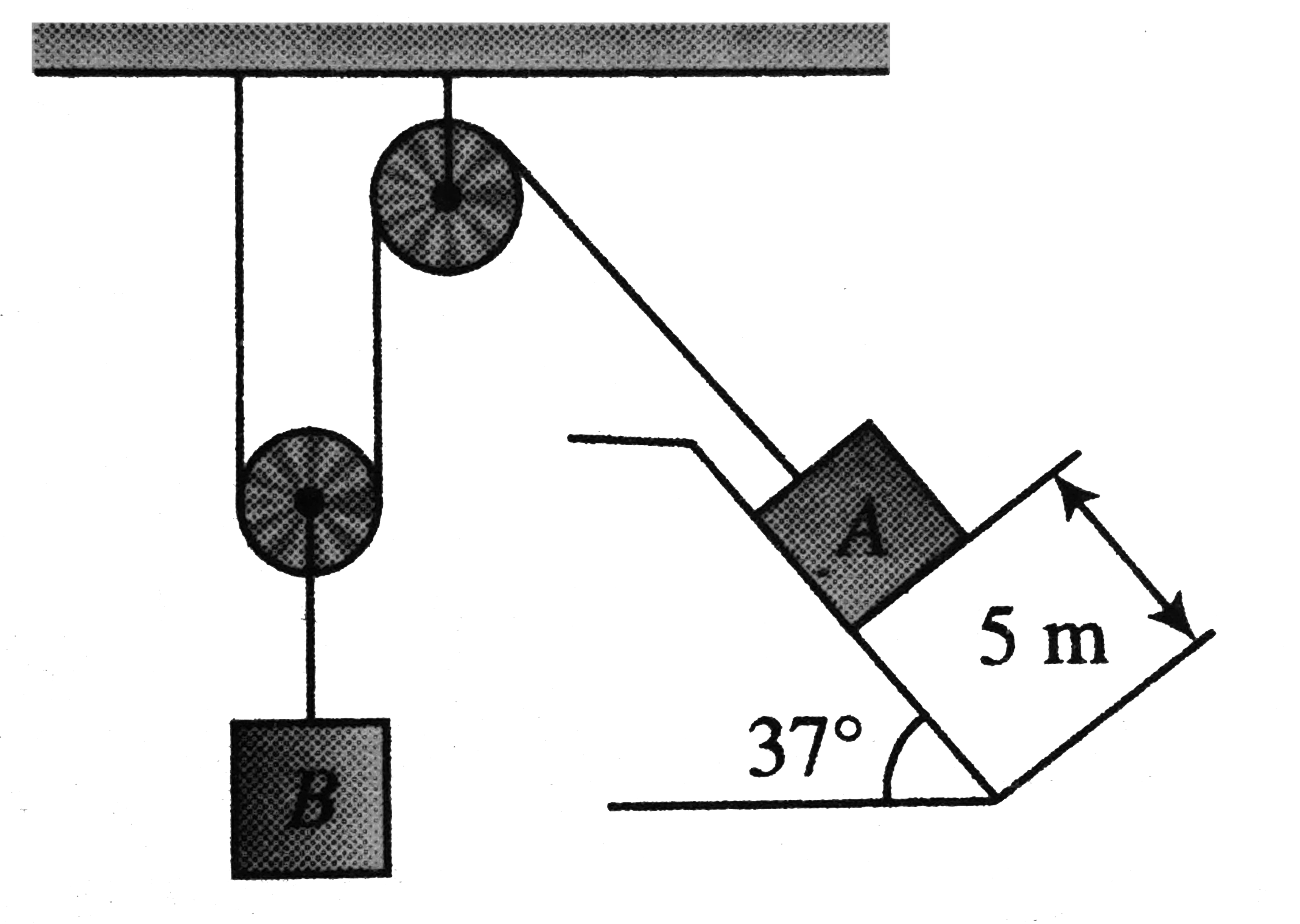 A(a) √32√gB(b) √34√gC(c) √g2√3D(d) √g2
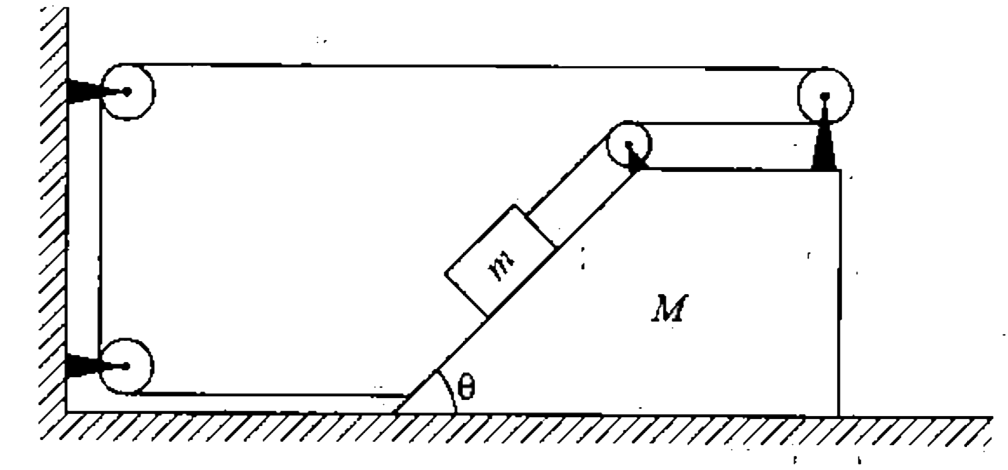
A(a) √32√gB(b) √34√gC(c) √g2√3D(d) √g2A smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is
 AmgcosθBless than mgcosθCgreater than mgcosθDmay be less or greater than mgcosθ depending upon whether M is less or greater than m
AmgcosθBless than mgcosθCgreater than mgcosθDmay be less or greater than mgcosθ depending upon whether M is less or greater than mAn arrangement is shown in figure. If all the surfaces are smooth and system is released from rest then the relation between accelerations of blocks P(ap)andQ(a_Q) will be
Aap=aQBap=4aQCap=2aQDap=aQ2
Blocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
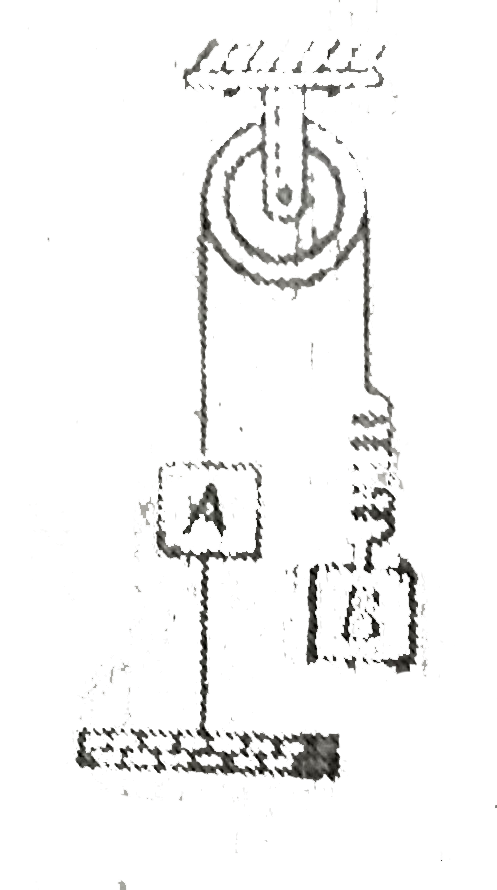
View SolutionThe pulley is light and smooth: the strings are inextensible and light. The system is released from rest, find the acceleration of each block, tensions in the strings and reaction in pulley.

View SolutionFigure-2.64 shows a block of mass M supporting a bar of mass m through a pulley system. If system is released from rest, find the acceleration of block M and the tension in the strings
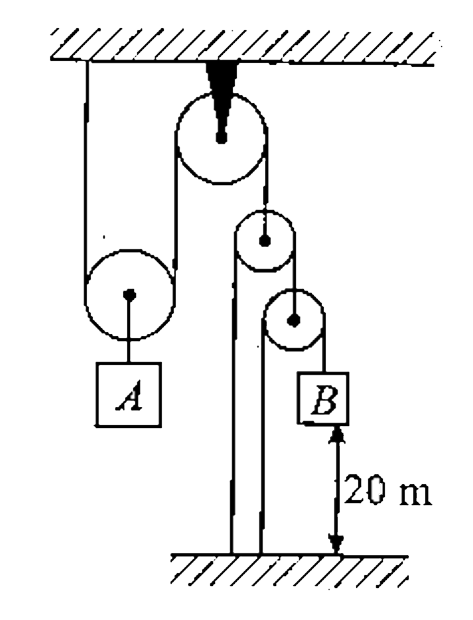
View SolutionIn the figure-2.216, the masses A and B are of 4kg and 12 kg respectively. When the system is released from rest, find the time after which the block B will hit the ground.
View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
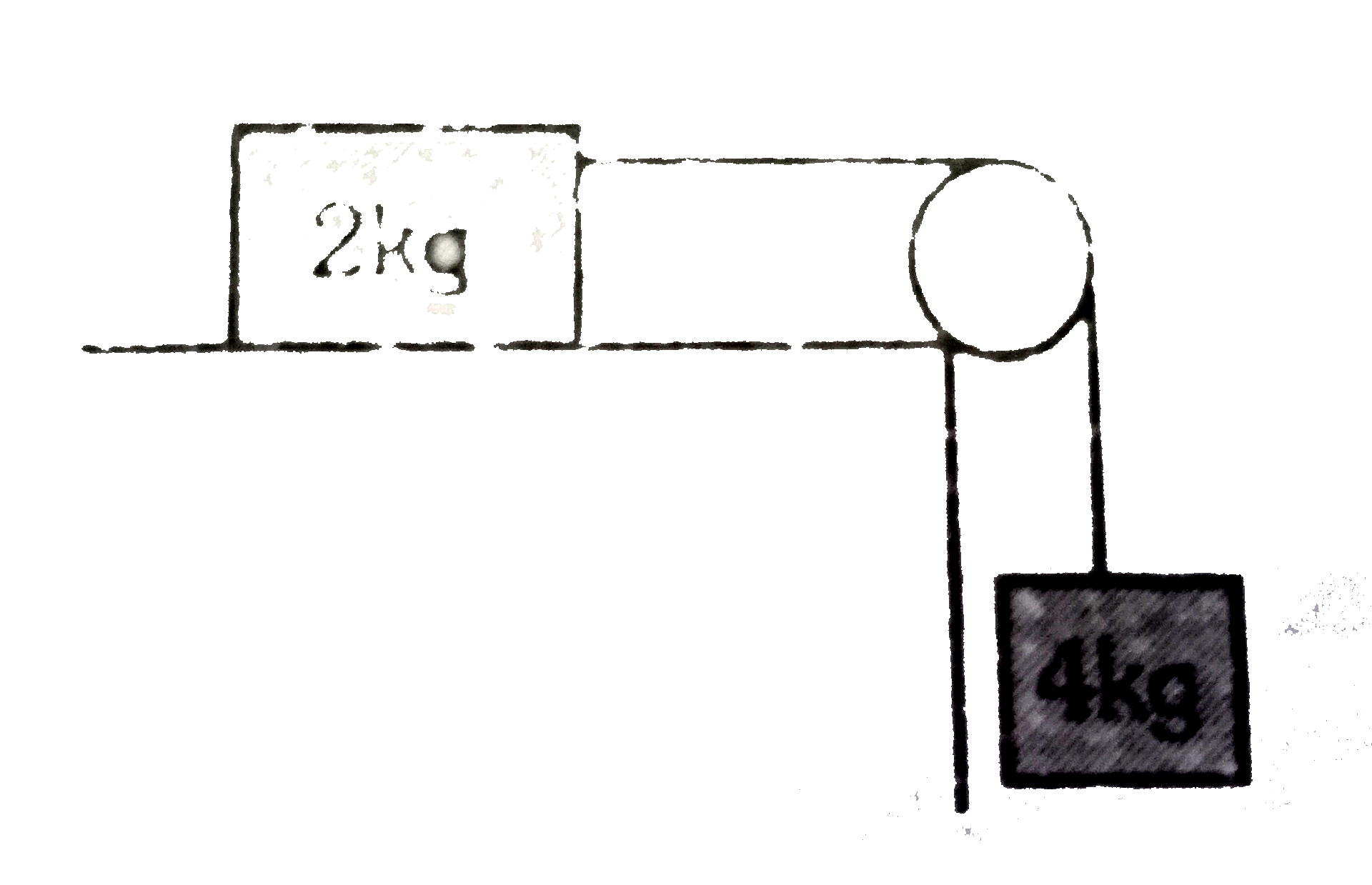
View Solution
