A heavy particle is projected with a velocity at an angle with the horizontal into the uniform gravitational field. The slope of the trajectory of the particle varies as




The correct Answer is:A
To solve the problem of how the slope of the trajectory of a heavy particle varies when projected at an angle with the horizontal, we can follow these steps:
1. Understanding the Problem:
We have a heavy particle projected with an initial velocity u at an angle θ with the horizontal. We need to find out how the slope of the trajectory changes.
2. Equation of Trajectory:
The equation of the trajectory of a projectile in a uniform gravitational field is given by:
y=xtanθ−gx22u2cos2θ
where:
- y is the height,
- x is the horizontal distance,
- g is the acceleration due to gravity,
- u is the initial velocity,
- θ is the angle of projection.
3. Finding the Slope:
To find the slope of the trajectory, we differentiate y with respect to x:
dydx=tanθ−gu2cos2θx
This expression represents the slope of the trajectory at any point x.
4. Analyzing the Slope:
The slope dydx is a linear function of x. The term −gu2cos2θx indicates that the slope decreases as x increases, since it has a negative coefficient.
5. Conclusion:
Therefore, the slope of the trajectory varies linearly with x and decreases as x increases. This means that the slope is negative and changes in a straight line manner.
Final Answer:
The slope of the trajectory of the particle varies linearly with x and is negative.
---
We have a heavy particle projected with an initial velocity u at an angle θ with the horizontal. We need to find out how the slope of the trajectory changes.
The equation of the trajectory of a projectile in a uniform gravitational field is given by:
y=xtanθ−gx22u2cos2θ
where:
- y is the height,
- x is the horizontal distance,
- g is the acceleration due to gravity,
- u is the initial velocity,
- θ is the angle of projection.
To find the slope of the trajectory, we differentiate y with respect to x:
dydx=tanθ−gu2cos2θx
This expression represents the slope of the trajectory at any point x.
The slope dydx is a linear function of x. The term −gu2cos2θx indicates that the slope decreases as x increases, since it has a negative coefficient.
Therefore, the slope of the trajectory varies linearly with x and decreases as x increases. This means that the slope is negative and changes in a straight line manner.
The slope of the trajectory of the particle varies linearly with x and is negative.
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Subjective
21 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
Knowledge Check
A heavy particle is projected with a velocity at an acure angle with the horizontal into a uniform gravitational field. The slope of the trajectory of the particle varies as
A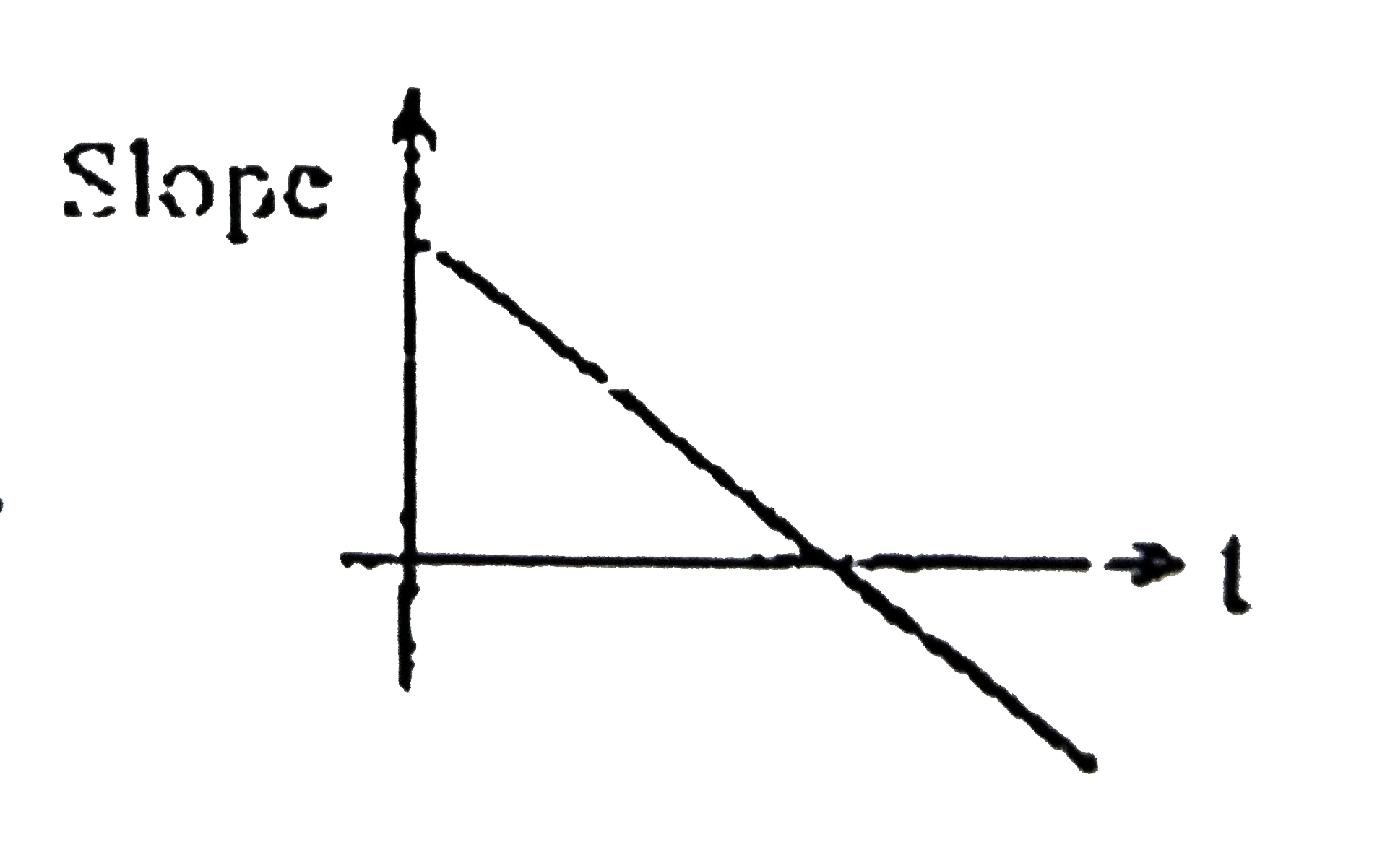 B
B C
C D
D
A particle is projected with a velocity '9m/sec' at an angle 450, with the horizontal.What is the radius of curvature of the trajectory of the particle at the position 'x=R/3' (R-Range of the projectile).
A3√20mB3√10C3√102mD34√10mA particle is projected with a velocity 8m/sec at an angle 450, with the horizontal.What is the radius of curvature of the trajectory of the particle at the instant of '14th' of the time of ascent.
A6.25mB12.5mC8mD10m
A particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA particle is projeced with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA particle is projected with initial velocity u making an angle α with the horizontal, its time of flight will be given by
View SolutionA particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
View SolutionA particle is projected with speed u at angle θ to the horizontal. Find the radius of curvature at highest point of its trajectory
View Solution